神经网络计算复杂度计算_图神经网络的计算复杂度解释

神经网络计算复杂度计算

Unlike conventional convolutional neural networks, the cost of graph convolutions is “unstable” — as the choice of graph representation and edges corresponds to the graph convolutions complexity — an explanation why.

与传统的卷积神经网络不同，图卷积的成本是“不稳定的”(因为图表示和边的选择对应于图卷积的复杂性)，这就是原因的解释。

Dense vs Sparse Graph Representation: expensive vs cheap?

密集vs稀疏图形表示法：昂贵还是便宜？

Graph data for a GNN input can be represented in two ways:

GNN输入的图形数据可以两种方式表示：

A) sparse: As a list of nodes and a list of edge indices

A)稀疏：作为节点列表和边缘索引列表

B) dense: As a list of nodes and an adjacency matrix

B)密集的：作为节点列表和邻接矩阵

For any graph G with N vertices of length F and M edges, the sparse version will operate on the nodes of size N*F and a list of edge indices of size 2*M.The dense representation in contrast will require an adjacency matrix of size N*N.

对于任何具有N个顶点(长度为F和M边)的图G，稀疏版本将在大小为N * F的节点上运行，并在边缘索引的大小为2 * M的列表上进行操作，而密集表示则需要邻接矩阵为尺寸N * N。

While in general the sparse representation is much less expensive in usage inside a graph neural network for forward and backward pass, edge modification operations require searching for the right edge-node pairs and possibly adjustment of the overall size of the list, which leads to variations on the RAM usage of the network. In other words, sparse representations minimize memory usage on graps with fixed edges.

虽然一般来说，稀疏表示在图神经网络内用于向前和向后传递的费用要便宜得多，但是边沿修改操作需要搜索右边的边节点对，并且可能需要调整列表的整体大小，这会导致变化网络的RAM使用情况。换句话说，稀疏表示将具有固定边缘的抓图上的内存使用降至最低。

While being expensive to use, the dense representation has the following advantages: Edge weights are naturally included in the adjacency matrix, edge modification can be done in a smooth manner and integrated into the network, finding edges and changing edge values does not change the size of the matrix. Those properties are crucial for Graph Neural Networks that rely on in network edge modifications.

尽管使用起来昂贵，但密集表示具有以下优点：边缘权重自然包含在邻接矩阵中，可以以平滑的方式进行边缘修改并将其集成到网络中，找到边缘和更改边缘值不会改变大小矩阵这些属性对于依赖网络边缘修改的图神经网络至关重要。

Taking GNN applications into perspective, the decision between sparse and dense representations can be formulated into two questions:

从GNN应用程序的角度来看，稀疏表示和密集表示之间的决策可以表述为两个问题：

Is there an advantage in computational complexity, i.e. What is the relation between the number of nodes and the number of edges per node or is 2*M much smaller than N*N
计算复杂度是否有优势，即节点数与每个节点的边数之间的关系是什么，或者比N * N小2 * M
Does the application require differentiable edge modifications
应用程序是否需要可区分的边缘修改

While the first question is straight forward to answer after inspection of the graphs, the second question depends on the structure of the neural network as well as the complexity of the graph. For now, it appears that large graphs (not talking about Toy examples here), benefit from pooling and normalisation/stabilization layers between layers of graph convolutions.

在检查完图形后，第一个问题很容易回答，而第二个问题取决于神经网络的结构以及图形的复杂性。目前看来，大型图(这里不讨论玩具示例)受益于图卷积层之间的合并和归一化/稳定化层。

Edges and complexity of convolution

卷积的边缘和复杂性

While some graphs arise naturally from data by well defined relations between nodes, for example an interaction graph of transactions between accounts in the last month, some more complex problem statements, especially for dense representations, do not naturally have a clear edge assignment for each vertex.

虽然有些图是通过节点之间定义明确的关系从数据中自然生成的，例如上个月帐户之间交易的交互图，但某些更复杂的问题陈述，尤其是对于密集表示而言，自然不会为每个顶点分配明确的边。

If the edge assignment is not given through the data, different edge variations will lead to different behaviour and memory costs of the graph neural network.

如果没有通过数据给出边缘分配，则不同的边缘变化将导致图神经网络的行为和存储成本不同。

For this, it makes sense to start with an array as a graph representation, this could be an image for example. For an array of size MxN, the smallest amount of edges that connects every node with every other node through several hops is through connecting the current node with previous and the next node. In this case there is M*N nodes and 2*M*N edges. A simple one hop convolution performs 2*M*N operations. However, this operation would be “slow” — in order for the node information in the middle of the array to reach the first node of the array, this would require around 0.5*M*N convolutions.

为此，从数组开始以图形表示是有意义的，例如，它可以是图像。对于大小为MxN的数组，通过几个跃点将每个节点与其他每个节点连接的边的最小数量是通过将当前节点与上一个和下一个节点连接。在这种情况下，有M * N个节点和2 * M * N个边。一个简单的单跳卷积执行2 * M * N个运算。但是，此操作将是“缓慢的”-为了使阵列中间的节点信息到达阵列的第一个节点，这将需要大约0.5 * M * N卷积。

A typical approach chosen for graph convolutions on images is to take the 8 direct neighbours for edge connection into accounts, in this case there is 8*M*N edges, hence each simple graph convolution has the cost of 8*M*N. For information from the center node of the array to reach the first node, being able to walk diagonally, this takes max(M,N) convolutions.

为图像上的图形卷积选择的一种典型方法是考虑8个直接相邻点进行边缘连接，在这种情况下，存在8 * M * N条边，因此每个简单的图形卷积的代价为8 * M * N。为了使信息能够从阵列的中心节点到达第一个节点(能够对角行走)，需要进行max(M，N)卷积。

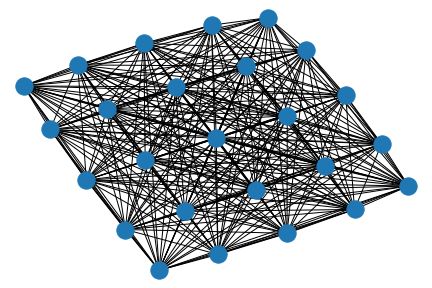
For so called self attention based approaches, every node would be connected to every other. While this requires (M*N)*(M*N) edges, during one convolutional operation the information of any node to any other node can be transmitted.

对于所谓的基于自我关注的方法，每个节点将彼此连接。尽管这需要(M * N)*(M * N)个边，但是在一次卷积操作期间，可以将任何节点的信息传输到任何其他节点。

From all of those three examples above, it becomes clear that the number of edges determines the complexity of the convolution. This is unlike conventional convolutional layers, where filter sizes often come in 3x3 format and are determined by the network design, not the image input.

从以上所有三个示例中，很明显，边的数量决定了卷积的复杂性。这与传统的卷积层不同，在传统的卷积层中，滤镜大小通常为3x3格式，并且由网络设计决定，而不是由图像输入决定。

Additional Info: Dense vs Sparse Convolutions

附加信息：密集与稀疏卷积

The choice of dense or sparse representation not only affects the memory usage, but also the calculation method. Dense and sparse graph tensors require graph convolutions that operate on dense or sparse inputs (or alternatively as seen in some implementations convert between sparse and dense inside the network layer). Sparse graph tensors would operate on sparse convolutions that use sparse operations. From a very naive point of view it would be logical to assume that dense computations would be more expensive but faster than sparse, because sparse graphs would require processing of operations in the shape of a list. However, libraries for sparse tensor operations are available for both PyTorch and Tensorflow that simplify and speed up sparse operations.

密集表示或稀疏表示的选择不仅会影响内存使用量，还会影响计算方法。密集和稀疏图张量需要在密集或稀疏输入上进行操作的图卷积(或者在某些实现中看到，在网络层内部在稀疏和稠密之间进行转换)。稀疏图张量将在使用稀疏运算的稀疏卷积上进行运算。从非常幼稚的角度来看，假设稀疏图将需要处理列表形式的运算，这将使密集计算比稀疏计算更昂贵但速度更快是合乎逻辑的。但是，PyTorch和Tensorflow都可以使用用于稀疏张量运算的库，这些库可以简化和加速稀疏运算。

Additional Info: Towards other edge criteria

附加信息：迈向其他边缘标准

From grid to k-nearest neighbours: If the graph’s nodes are not arranged in a grid as in the example images, a generalization of this approach is to find the k-nearest neighbors for each node. This approach can be further generalized by using feature point input instead of positions as node coordinates, with the “distance” function in the k-nn set up serving as a similarity measurement between features.

从网格到k个近邻：如果图的节点未如示例图像中那样排列在网格中，则此方法的一般化方法是为每个节点找到k个近邻。通过使用特征点输入而不是位置作为节点坐标，可以进一步推广这种方法，其中k-nn中的“距离”函数设置为特征之间的相似性度量。

From Euclidean distance to other evaluation methods: While some graph network applications benefit from physical coordinates or pixel positions (such as traffic prediction or image analysis), other graphs and edge relations might arise from similarity criteria based on connections or knowledge, such as social networks or transaction graphs.

从欧几里得距离到其他评估方法：尽管某些图形网络应用受益于物理坐标或像素位置(例如流量预测或图像分析)，但其他图形和边缘关系可能来自基于联系或知识的相似性标准，例如社交网络或交易图。

Related resources:

神经网络计算复杂度计算_图神经网络的计算复杂度解释

你可能感兴趣的:(神经网络,python,leetcode,机器学习,算法)