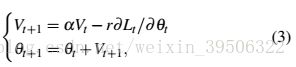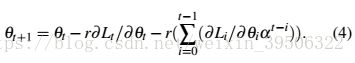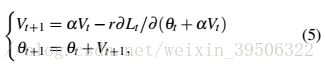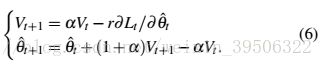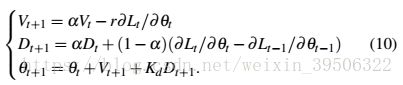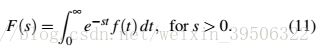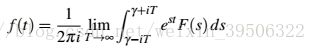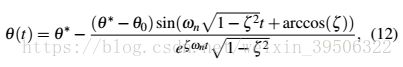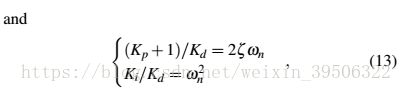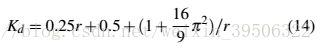论文翻译：A PID Controller Approach for Stochastic Optimization of Deep Networks——一种用于深度网络随机优化的PID控制器方法

Abstract

Deep neural networks have demonstrated their power in many computer vision applications. State-of-the-art deep architectures such as VGG, ResNet, and DenseNet are mostly optimized by the SGD-Momentum algorithm, which updates the weights by considering their past and current gradients. Nonetheless, SGD-Momentum suffers from the overshoot problem, which hinders the convergence of network training. Inspired by the prominent success of proportional-integral-derivative (PID) controller in automatic control, we propose a PID approach for accelerating deep network optimization. We first reveal the intrinsic connections between SGD-Momentum and PID based controller, then present the optimization algorithm which exploits the past, current, and change of gradients to update the network parameters. The proposed PID method reduces much the overshoot phenomena of SGD-Momentum, and it achieves up to 50% acceleration on popular deep network architectures with competitive accuracy, as verified by our experiments on the benchmark datasets including CIFAR10,CIFAR100, and Tiny-ImageNet.
 

摘要

深层神经网络已经在许多计算机视觉应用中展示了它们的力量。最先进的深度架构，如VGG、ResNet和DenseNet，主要是通过SGD-Momentum算法进行优化的，该算法通过考虑它们的过去和当前的梯度来更新权重。尽管如此，SGD-Momentum受到了超调问题的影响，这阻碍了网络训练的收敛。在自动控制中比例-积分-微分（PID）控制器的显著成功的启发下，提出了一种加速深度网络优化的PID方法。我们首先揭示了sgd-Momentum算法和PID控制器之间的内在联系，然后给出了利用过去的、现在的和梯度的变化来更新网络参数的优化算法。所提出的PID方法减少了SGD-Momentum的超调现象，并且在流行的深网络架构上达到了50%的加速，具有竞争的准确性，我们在基准数据集上的实验验证了这一点，包括CIFAR10、CIFAR100和Tiny-ImageNet。

 

1. Introduction

Benefitting from the availability of large-scale visual datasets such as ImageNet [1], deep neural networks (DNN), especially deep convolutional neural networks (CNNs), have significantly improved the system accuracy in many computer vision problems, such as image classi-fication [2], object detection [3], and face recognition [4],etc. Despite the great successes of deep learning, the training of deep networks on large-scale datasets is usually computationally expensive, costing several days or even weeks using GPU equipped high-end PCs. It is substantially important to investigate how to accelerate the training speed of deep models without sacrificing the accuracy, which can save the time and memory cost, particularly for resource limited applications.
从ImageNet 、深层神经网络（DNN）、特别是深层卷积神经网络（CNNs）等大规模可视化数据集的可用性中获益，极大地提高了许多计算机视觉问题的系统精度，如图像分类、目标检测和人脸识别等。尽管深度学习取得了巨大的成功，但在大型数据集上对深度网络的训练通常是非常昂贵的，使用GPU装备的高端个人电脑花费了几天甚至几周的时间。重要的是要研究如何在不牺牲准确性的前提下加速深度模型的训练速度，这可以节省时间和内存成本，特别是对于资源有限的应用程序来说。

The key component of DNN training is the optimizer,which defines how the millions or even billions of parameters of a deep model are updated. The learning rate is one of the most important hyper-parameters to train a DNN [5].Based on how the learning rate is set, deep learning optimizers can be categorized into two groups, hand-tuned learning rate optimizers such as stochastic gradient descent (SGD) [6], SGD Momentum [7] and Nesterov's Momentum [7], and auto learning rate optimizers such as AdaGrad [8], RMSProp [9] and Adam [10], etc. Auto learning rate optimizers adaptively tune an individual learning rate
for each parameter. Such a goal of fine adaptation is attractive and it is expected to yield better deep model learning results. However, the recent findings by Wilson et al. [11] show that hand-tuned SGD-Momentum achieves better result at the same speed or even faster speed. The hypothesis put forth here is that adaptive methods may converge to different local minima [12]. It is also noted that most of the best-performance deep models such as ResNet [13] and DenseNet [14] are usually trained by SGD-Momentum.
DNN训练的关键组成部分是优化器，它定义了深度模型的数百万甚至数十亿个参数是如何更新的。学习速率是训练DNN 的最重要的超参数之一。在学习速率是如何设置的基础上,深度学习优化器可以分为两组,手动调整学习速率优化等随机梯度下降法(SGD)，SGD Momentum和Nesterov's Momentum,和自动学习速率优化器如AdaGrad,RMSProp和Adam等。自动学习速率优化器为每个参数自适应优化各自的学习速率。这种有着良好适应的目标是有吸引力的，它有望产生更好的深度模型学习效果。然而，威尔逊等人最近的发现表明，手动调节的SGD-Momentum可以以相同的速度或更快的速度获得更好的结果。这里提出的假设是，自适应方法可能收敛于不同的局部最小值。还注意到，大多数性能最好的深层模型，如ResNet 和DenseNet ，通常都是通过SGD-Momentum算法来训练的。

The strategy of SGD-Momentum is to consider both the past and present gradients to update the network parameters. However, SGD-Momentum suffers from the overshoot problem [15], which refers to the phenomena that a weight's value exceeds much its target value and does not change its update direction. Such an overshoot problem hinders the convergence of SGD-Momentum, and costs more training time and resources. It is of significant importance to investigate whether we can design a new DNN optimizer which is free of overshoot problem and has faster convergence speed while maintaining good accuracy.
SGD-Momentum的策略是考虑过去和现在的梯度来更新网络参数。然而，SGD-Momentum受到了超调问题的影响，它指的是权重的值超过其目标值的现象，并且不会改变它的更新方向。这样的超调问题阻碍了SGD-Momentum的收敛，并且花费了更多的训练时间和资源。研究是否能设计出一种新的DNN优化器，它不受超调问题的影响，并且具有更快的收敛速度，同时保持良好的准确性，这是非常重要的。

It has been found that many optimization algorithms popularly employed in machine learning studies share certain similarity to those classic control methods studied since 1950s [16]. In literature of automatic control, the feedback control system plays a key role, while the proportionalintegral-derivative (PID) controller is the most commonly used feedback control mechanism due to its simplicity, functionality, and broad applicability [17]. More than 90% of industrial controllers are implemented based on PID [18],including self-driving car [19], unmanned flying vehicles [20], robotics [21], etc. The basic idea of PID control is that the control action should be proportional to the current error (the difference between system output and desired output), the integral of the past error over time, and the derivative of the error, which represents future trend.
研究发现，在机器学习研究中普遍采用的许多优化算法与自20世纪50年代以来研究的经典控制方法有一定的相似性。在自动控制的文献中，反馈控制系统起着关键的作用，而比例-积分-导数（PID）控制器是最常用的反馈控制机制，因为它的简单性、功能性和广泛的适用性。超过90%的工业控制器实现基于PID,包括无人驾驶汽车,无人驾驶的飞行汽车,机器人等。PID控制的基本思想是控制动作应正比于当前的误差(系统输出与期望输出值之间的误差),随着时间的推移的过去的积分误差,和代表未来趋势的误差的导数。

Though PID controller has gained massive successes in different industries of control and automation, little study has been done on its connections with stochastic optimization, as well as its potential applications to DNN training.In this paper, we make the first attempt along this line. We first bridge the gap between PID controller and stochastic optimization methods such as SGD, SGD-Momentum and Nesterov's Momentum, and consequently develop a PID approach for DNN optimization. Compared with SGDMomentum which utilizes the past and current gradients,the proposed PID optimization approach also utilizes the gradient changes to update the network. We further introduce the Laplace Transform [22] to initialize the hyperparameter introduced in our method, resulting in a simple yet effective stochastic DNN optimization algorithm. The major contributions of this work are summarized as follows.

虽然PID控制器在不同的控制和自动化领域取得了巨大的成功，但对其与随机优化的联系以及它对DNN训练的潜在应用进行了很少的研究。在这篇文章中，我们第一次尝试这个思路。我们首先将PID控制器与随机优化方法之间的差距进行了对接，如SGD、SGD-Momentum和Nesterov's Momentum，从而为DNN优化设计了一种PID方法。与利用过去和当前梯度的SGD-Momentum相比，提出的PID优化方法也利用梯度变化来更新网络。我们进一步介绍了拉普拉斯变换来初始化我们方法中引入的超参数，得到了一个简单而有效的随机DNN优化算法。这一工作的主要贡献总结如下。

• By linking the calculation of errors in feedback control system and the calculation of gradient in network updating, we reveal the intrinsic connections between deep network optimization and feedback system control, and show that SGD-Momentum is a special case of PID controller with only proportional (P) and integral (I) components.
• We then propose a PID approach to optimize DNN by utilizing the present, past and changing information of the gradient. The classical Laplace Transform is introduced to understand and initialize the hyper-parameter in our algorithm.
• We systematically evaluate the proposed approach, and the extensive experiments on CIFAR10, CIFAR100 and Tiny-Imagenet datasets demonstrate the efficiency and effectiveness of our PID approach.
• The rest of this paper is organized as follows. Section 2 briefly reviews related work. Section 3 connects PID controller with DNN optimization. Section 4 introduces the proposed PID approach for DNN optimization. Experimental results and detailed analysis are reported in Section 5.Section 6 concludes this paper.
   
• 通过对反馈控制系统中误差的计算和网络更新中梯度的计算，揭示了深层网络优化与反馈系统控制之间的内在联系，并证明了SGD-Momentum是一种只有比例（P）和积分（I）分量的PID控制器的特殊情况。
• 然后，我们提出了一种优化DNN的PID方法，利用了当前的、过去的和变化的梯度信息。在算法中引入经典的拉普拉斯变换，以便理解和初始化超参数。
• 我们系统地评估了所提议的方法，并对CIFAR10、CIFAR100和Tiny-Imagenet数据集进行了广泛的实验，证明了我们的PID方法的效率和有效性。
• 本文的其余部分按如下方式组织。第2节简要回顾相关工作。第3节将PID控制器与DNN优化连接起来。第4节介绍了用于DNN优化的PID方法。实验结果和详细分析报告在第5节中。第6节总结了这篇论文。

 

2. Related Work

2.1. Deep Learning Optimization

The learning rate is the most important hyper-parameter to train deep neural networks [9]. Based on how the learning rate is set, two classes of deep learning optimization methods can be categorized. The first class indicates fixed learning rate methods such as SGD [6], SGD Momentum [7],and Nesterov0s Momentum [7], etc., and the second class includes auto learning rate methods, such as AdaGrad [8],RMSProp [9], and Adam [10], etc. Our work is based on fixed learning rate methods considering that the current state-of-the-art results on CIFAR10, CIFAR100, ImageNet,PASCAL VOC and MS COCO datasets were mostly obtained by Residual Neural Networks [13, 14, 23, 24] trained by use of SGD Momentum.
学习速率是训练深层神经网络的最重要的超参数。基于学习速率的设置，可以对两类深度学习优化方法进行分类。第一种分类表明固定学习速率方法如SGD,SGD-Momentum,和Nesterov's Momentum等等,第二种分类包括自动学习速率的方法,如AdaGrad,RMSProp,和Adam,等等。我们的工作是基于固定的学习速率方法，考虑到当前在CIFAR10,CIFAR100,ImageNet,PASCAL VOC和MS COCO数据集最先进的结果大多是利用SGD Momentum算法通过残差神经网络训练的。

Stochastic Gradient Descent (SGD) [6] is a widely used optimization algorithm for machine learning in general, especially for deep learning. SGD usually uses a fixed learning rate. This is because the SGD gradient estimator introduces a source of noise (the random sampling of m training examples), and that noise does not vanish even when the loss arrives at a minimum.
随机梯度下降（SGD）是一种广泛应用于机器学习的优化算法，特别是对深度学习而言。SGD通常使用固定的学习速率。这是因为SGD梯度估计器引入了噪声源（从m个训练示例中随机抽样），而且即使损失达到最小，噪声也不会消失。

SGD Momentum [7] is designed to accelerate learning,especially in the case of small and consistent gradients.The momentum algorithm accumulates an exponentially decayed moving average of past gradients and continues to move in the consistent direction. The name momentum derives from a physical analogy, in which the negative gradient is a force moving a particle through parameter space. A hyper-parameter  determines how much the past gradients to the current update of the weights.
SGD Momentum是为了加速学习，特别是在小而一致的梯度的情况下。动量算法累积过去梯度的指数衰减移动平均值并继续沿一致方向移动。这个名字的动量来自于一个物理类比，在这个类比中，负梯度是一种通过参数空间移动粒子的力。一个超参数决定了过去的梯度到当前权重的更新有多少。

Nesterov's Momentum [7] is a variant of the momentum algorithm that was motivated by Nesterov's accelerated gradient method [25]. The difference between Nesterov momentum and regular momentum lies on where the gradient is evaluated. With Nesterov's momentum, the gradient is estimated after the current velocity is applied.Thus one can interpret Nesterov's momentum as attempting to add a correction factor to the standard method of momentum. Recently, Nesterov's Momentum method has been characterized as a second order ordinary differential equation in the small step limit [26].
Nesterov's Momentum是动量算法的一个变体，它是出于Nesterov的加速梯度法。Nesterov momentum和常规动量的区别在于梯度被评估的位置。利用Nesterov momentum，在应用当前速度之后，估计梯度。因此，人们可以将Nesterov的动量解释为试图给标准的动量方法增加一个修正因子。最近，Nesterov momentum算法被描述为在小步限制中的二阶常微分方程。

 

2.2. PID Controller

The PID controller exploits the present, past and future information of prediction error to control a feedback system [18]. PID based controller originates in the 19th century for speed control. The theoretical foundation for the operation of PID was first described by Maxwell in 1868 in his seminal paper “On Governors” [27]. Minorsky [28] then gave this a mathematical formulation. Over the years,many advanced control algorithms have also been proposed.However, most industrial controllers are implemented with a PID algorithm because it is simple, robust and easy to use [29]. A PID controller continuously calculates an error e(t), which is the difference between the desired optimal output and a measured system output, and applies a correction u(t) to the system based on the proportional (P), integral (I), and derivative (D) terms of e(t). Mathematically,there is:

where Kp, Ki and Kd are the gain coefficients on the P, I and D terms, respectively.

PID控制器利用当前的、过去的和未来的预测误差信息来控制反馈系统。基于PID的控制器起源于19世纪的速度控制。1868年，麦克斯韦尔在他影响深远的“On Governors” 论文中首次描述了PID操作的理论基础。然后，Minorsky 给出了一个数学公式。多年来，也提出了许多先进的控制算法。然而，大多数工业控制器都是用PID算法实现的，因为它简单、健壮且易于使用。一个PID控制器不断地计算一个误差e（t），它是期望的最优输出和一个测量系统输出之间的差值，并根据比例（P）、积分（I）和e（t）的导数（D）项对系统进行校正u（t）。在数学上,

Kp，Ki和Kd分别是比例P，积分I和微分D的增益系数。

One can see that the error e(t), defined as the difference between the desired value and the actual output, has the same spirit as the gradient used in deep learning optimization. The coefficients Kp, Ki and Kd determine the contributions of present, past and future errors to the current correction. Such analyses inspire us to adapt the PID control techniques to the field of deep network optimization. To the best of our knowledge, we are the first to introduce the idea of PID into the field of deep learning as a new optimizer. As we will see later in this paper, the proposed optimizer inherits fantastic advantages of PID controller and stays simple and efficient.

我们可以看到，误差e（t），定义为期望值与实际输出之间的差，与深度学习优化中使用的梯度具有相同的精髓。系数Kp、Ki和Kd决定了当前、过去和未来的误差对当前修正的贡献。这些分析使我们能够将PID控制技术应用到深度网络优化领域。据我们所知，我们是第一个将PID的概念引入到深度学习领域的新优化器。正如我们将在本文后面看到的，建议提出的优化器继承了PID控制器的巨大优势，保持其简单和高效性。

 

3. PID and Deep Network Optimization

In this section, we disclose the connections between PID control and SGD based deep optimization. Such connections motivate us to propose a new optimization method to accelerate the training of DNNs. Updating the weights in a deep network can be viewed as deploying many PID controllers to drive the system to reach an equilibrium.

在本节中，我们将揭示PID控制和基于SGD的深度优化之间的联系。这样的联系促使我们提出一种新的优化方法来加速DNNs的训练。在一个深度网络中更新权重可以被看作是配置许多PID控制器来驱动系统达到平衡。

3.1. General Connections

In Figure 1, we show the flowchart of a PID controller based feedback control system, and the flowchart of SGDMomentum based DNN optimization. The goal of a control system is to measure the output system status consecutively and update it to the desired status by using a control unit.In feedback control, the output will affect the input quantity, and the controller will make appropriate updates of the system status based on the error e(t) between the measured system status and the desired status. To reach this goal, the PID controller computes a control variable u(t) based on the current, past and future (i.e., derivative) of the error e(t), as shown in Eq. (1).

在图1中，我们展示了一个基于PID控制器的反馈控制系统的流程图，以及基于SGD Momentum 的DNN优化的流程图。控制系统的目标是通过使用控制单元来连续地测量输出系统状态，并将其更新到所需的状态。在反馈控制中，输出将影响输入量，控制器将根据测量系统状态和期望状态之间的错误e(t)对系统状态进行适当的更新。为了达到这个目标，PID控制器根据当前、过去和未来（例如，导数）的误差e(t)计算一个控制变量u(t)，如Eq(1)。

Deep learning aims to learn an approximation function or mapping function  with parameters  to map the input x to the desired output y, i.e., , assuming that there are (complex) relationships or causality between  and .With enough training data, deep learning can train a network with millions of parameters (weights ) to fit those complex relationships which cannot be formulated using analytical functions. Usually, a loss function  will be defined based on the desired output y and the predicted output to measure whether the goal is reached. The loss affects the weights by performing “backward propagation of errors” [30]. That is, it distributes the error to each node by calculating the gradients of weights. If the loss  is not small enough, the network will update its weights  based on the gradients . Therefore, it is reasonable to associate the “error” in PID control with the “gradient” in DL. This procedure is iterated till  converges or is small enough. Many optimizers have been proposed to minimize the loss  by updating  using the gradients , including SGD, SGD-Momentum, Adam, etc.
深度学习的目的是学习一个近似函数或映射函数，用参数来映射输入x到期望的输出y，等等，，假设x和y之间存在（复杂的）关系或因果关系。有了足够的训练数据，深度学习可以训练一个拥有数百万个参数（权重）的网络来适应那些不能用分析功能来制定的复杂关系。通常，一个损失函数将根据期望的输出y和预期的输出来定义，以测量是否达到目标。通过执行误差的反向传播，损失会影响权重。也就是说，它通过计算权重的梯度来将误差分配给每个节点。如果损失不够小，网络将根据梯度更新它的权值，因此，将PID控制中的误差与DL中的梯度联系起来是合理的。这个过程是迭代的，直到收敛或者足够小。通过使用梯度来更新，包括SGD、SGD-Momentum、Adam等，已经提出了许多优化器来最小化损失。

From the above discussions, we can see that deep network optimization shares high similarity to PID based control. Both of them update the system/network based on the difference/loss between actual output and desired output. The feedback in PID control corresponds to the backpropagation in network optimization. The major difference is that the PID controller computes the update using system error , while deep network optimizers determines the updates based on gradient . If we view gradient as the incarnation of error , PID controller can be fully connected with DNN optimization. In the following, we will see that SGD, SGD-Momentum and Nesterov's Momentum all can be explained as a kind of PID controller.
从以上讨论中，我们可以看到，深度网络优化与PID控制具有很高的相似性。它们都基于实际输出和期望输出之间的差异/损失来更新系统/网络。PID控制中的反馈与网络优化中的反向传播相对应。主要的区别在于，PID控制器使用系统误差来计算更新，而深度网络优化器根据梯度来确定更新，如果我们将梯度视为误差的化身，PID控制器可以与DNN优化完全连接。在下面，我们将看到SGD，SGD-Momentum和Nesterov's Momentum都可以解释为一种PID控制器。

 

3.2. SGD is a P Controller

SGD and its variants are probably the most widely used optimization algorithms for DNN optimization. The parameter update rule of SGD from time (i.e., iteration)  to time  is given by:

SGD及其变体可能是最广泛使用的用于DNN优化的优化算法。从时间到时间（即：迭代），SGD的参数更新规则是由以下公式给出：

where  is the learning rate. By viewing the gradient as error , and comparing Eq. (2) to PID controller in Eq. (1), one can see that SGD only uses the present gradient to update the weights. It is a type of P controller with .

是学习速率。通过将梯度视为误差，并将Eq.(2)与Eq(1)的PID控制器进行比较，我们可以看到SGD只使用当前的梯度来更新权重。它是一种带有的P控制器。

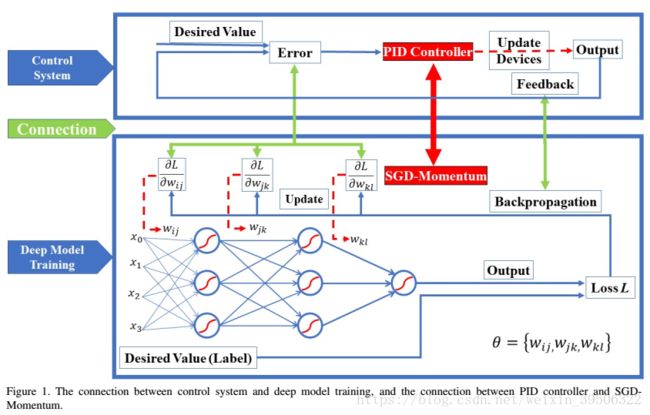
图1所示。控制系统与深度模型训练之间的联系，以及PID控制器与SGD Momentum之间的联系。

 

3.3. Momentum Optimization is a PI Controller

SGD-Momentum is able to reach the objective more quickly than SGD along the small but consistent directions,resulting in a faster convergence speed. Its parameter update rule is given by:

在小而一致的方向上，SGD-Momentum能够比SGD更快地到达目标，从而导致更快的收敛速度。它的参数更新规则由以下公式给出：

where   is the accumulation of history gradient, and  is the rate of moving average decay.

在是历史梯度的积累，而是移动平均衰变的速率。
With some mathematical tricks (Sum Formula for a Sequence of Numbers [31]), we can remove from Eq. (3),and rewrite the update rule as:

使用一些数学技巧（数字序列的求和公式），我们可以从Eq.（3）中删除，并将更新规则重写为：

One can see that the update of parameters relies on both the present gradient () and the integral of past gradients 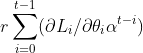. The only difference is that there is a decay term  in the  term. This difference is because deep learning algorithms use a mini-batch of training examples to compute the gradient, and thus the gradients are stochastic. The introduction of decay term  is to forget the gradients far away from present to reduce noise. Overall,SGD-Momentum can be viewed as a PI controller.
我们可以看到，参数的更新依赖于现在的梯度和过去梯度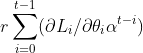的积分。唯一的区别是在项中有一个衰减项。这种差异是因为深度学习算法使用了一小批训练样本来计算梯度，因此梯度是随机的。衰变项的引入是为了忘记远离现在的梯度以减少噪声。总的来说，SGD-Momentum可以看作是PI控制器。

 

3.4. Nesterov0s Momentum Optimization is a PI Controller with larger P

The Nesterov's Momentum update rule is given by:

Nesterov的动量更新规则是由：

By using a variable transform , and expressing the update rule in terms of  , we have:

通过使用变量转换，并以的形式表示更新规则，我们有：

Again, by using the Sum Formula for a Sequence of Numbers [31], we can have (the detailed derivation can be found in the supplementary file):

同样，通过使用数字序列的求和公式，我们可以得到（详细的推导可以在补充文件中找到）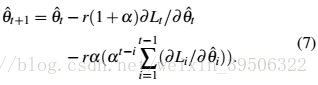

One can see that like SGD-Momentum, the Nesterov's Momentum also uses the present gradient and integral of past gradients to update the parameters, while the gain coefficient Kp is larger than that in SGD-Momentum.

你可以看到，像SGD-Momentum一样，Nesterov的动量也使用了现在的梯度和过去梯度的积分来更新参数，而增益系数比SGD-Momentum大。

 

4. PID based Deep Optimization

4.1. The Overshoot Problem of SGD-Momentum

From Eq. (4) and Eq. (7), one can see that the Momentum will accumulate history gradients. However, if the weights should change their descending direction, the history gradients will lag the update of weights. Such a phenomenon caused by history gradient is called overshoot,which is defined in discrete-time control systems [15] as”the maximum peak value of the response curve measured from the desired response of the system”. Mathematically,it is defined as:

从Eq（4）和Eq（7）中，你可以看到动量将积累历史梯度。然而，如果权重改变它们的下降方向，那么历史梯度将会滞后于权重的更新。由历史梯度引起的这种现象被称为超调，它在离散时间控制系统中被定义为从系统的期望响应中测量的响应曲线的最大峰值。在数学上，它被定义为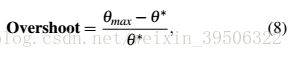

where  and  are the maximum and optimum values of the weight, respectively.

和分别是权重的最大值和最优值。
One commonly used test benchmark of overshoot is the first function of De Jong's [32] because it is smooth, unimodal, and symmetric. The function can be defined as , whose search domain is ,. There is no local minimum but a global minimum of this function: .

一种常用的超调测试基准是De Jong's的第一个函数，因为它是平滑的、单模态的和对称的。函数可以定义为，其定义域为,。这里没有局部最小值，而是这个函数的全局最小值：。

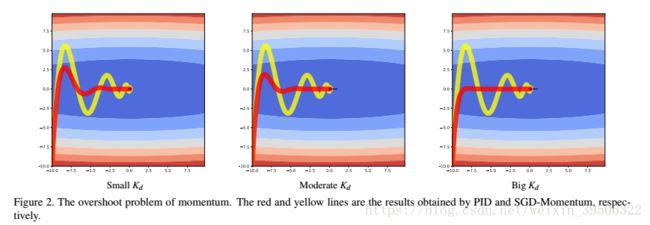
We add a derivative (change of gradient) term to SGDMomentum to build a simple PID optimizer:

我们在SGDMomentum中添加一个导数（梯度变化）项来构建一个简单的PID优化器：

where  is the current iteration number for . The simulation results by setting different values of  in Eq. (9) are illustrated in Figure 2. The background is the loss-contour map; the redder, the bigger the loss value is, and the bluer,the smaller the loss value is. The x-axis and y-axis denote  and , respectively. Both and are initialized to -10. The yellow line shows the optimization route of SGD-Momentum, and the red line shows the route of PID optimizer. One can see that SGD-Momentum has obvious overshoot problem. With the set to 0:1, 0:5 and 0:93,respectively, the PID optimizer exploits more ”future” error
(the change of gradients), and largely reduces the overshoot problem.

是当前的迭代次数，通过在Eq(9)中设置不同的Kd值，如图2所示。背景是损失等值线图;越红，损失值越大，越蓝，损失值越小。x轴和y轴分别表示和。和都被初始化为-10。黄色线显示了SGD-Momentum的优化路线，红线显示了PID优化器的路线。我们可以看到，SGD-Momentum有明显的超调问题。随着Kd设置为0.1、0.5和0.93，PID优化器利用了更多的未来误差（梯度的变化），并在很大程度上减少了超调问题。

 图2。动量的超调问题。红线、黄线分别是由PID和SGD-Momentum获得的结果。

 

4.2. PID Optimizer for DNN

The toy example in Section 4.1 motivates us to propose a PID optimizer to accelerate the training of DNN. As we show in Eq. (4), SGD-Momentum is actually a PI controller which uses present and past gradient information. By adding a derivative term to introduce the future information,a PID controller can effectively reduce the overshoot problem, as shown in Figure 2. Considering that the training of deep models is usually in a mini-batch based manner, which may introduce noise in the computing of gradients, we also compute the moving average of the derivative part. The proposed PID optimizer updates parameter  at iteration by:

第4.1节中的示例推动我们提出一个PID优化器来加速对DNN的训练。正如我们在Eq(4)中显示的那样，SGD-Momentum实际上是一个PI控制器，它使用现在和过去的梯度信息。通过添加一个微分项来引入未来信息，PID控制器可以有效地减少超调问题，如图2所示。考虑到深度模型的训练通常是以一种小批量的方式进行的，这可能会在梯度计算中引入噪声，我们还计算了导数部分的移动平均值。建议的PID优化器在迭代中更新参数

As can be seen from Eq. (10), however, our optimizer introduces a hyperparameter  compared with SGDMomentum. Fortunately, this hyper-parameter Kd can be well initialized by employing the theory of Laplace Transform [22] with Ziegler-Nichols [33] tuning method, as we describe in the following section.

从Eq(10)可以看出，与SGDMomentum相比，我们的优化器引入了一个超参数。幸运的是，这个超参数可以通过使用拉普拉斯变换和Ziegler-Nichols 调优方法进行很好的初始化，正如我们在下面的部分中所描述的那样。

 

4.3. Initialization of Hyper-parameter Kd

The Laplace Transform converts the function of real variable  (time) to a function of complex variable  (frequency).Denote by  the Laplace transform of . There is

拉普拉斯变换将实变量（时间）的函数转换为复变量（频率）的函数。用表示的拉普拉斯变换。有

Usually is easier to solve than , and can be recovered from by the Inverse Laplace transform:

通常比更容易解，可以从拉普拉斯逆变换中恢复：

where  is a real number and  is the unit of imagery part.In practice, we could decompose a Laplace transform into known transforms of functions in the Laplace table [34],which includes most of the commonly used Laplace transforms, and then construct the inverse transform. With Laplace Transform, we can convert the PID optimizer into its Laplace transformed functions of , and then simplify the algebra. Once we find the transformed solution of , we can inverse the transform to obtain the required solution  as a function of .

是一个实数，是图像部分的单位。在实践中，我们可以将拉普拉斯变换分解为拉普拉斯表中已知的函数变换，其中包括大多数常用的拉普拉斯变换，然后构造逆变换。通过拉普拉斯变换，我们可以把PID优化器转换成的拉普拉斯变换函数，然后简化代数运算。一旦我们找到了的变换后的解，我们就可以逆变换以得到所需的解作为的函数。
A weight of a deep model node is initialized as a scalar , and it is updated iteratively to reach its optimal value denoted by . Then the optimization of each weight in DNN can be simplified as a step response (from to ) in control theory. We can use the Laplace Transform as a guide to set . Denote by  the time domain change of weight . After some mathematical derivation (please refer to our supplementary file for the detailed derivation process), we have:

一个深度模型节点的权重被初始化为一个标量，并且它被迭代地更新以达到它的最优值，由表示。然后，在控制理论中，在DNN中每一个权重的优化可以简化为一个阶跃响应（从到）。我们可以用拉普拉斯变换作为设置的指引。用表示权重的时间域变化。在一些数学推导之后（请参阅我们的补充文件以获得详细的推导过程），我们有

where  and  are damping ratio and natural frequency of the system, respectively. In Figure 3, we show the evolution process of a weight as an example of . From Eq. (13),we have . One can see that  is a monotonically decreasing function of . Refer to the definition of overshoot in Eq. (8), one can see that is monotonically decreasing with overshoot. Then  is a monotonically increasing function of overshoot. So more history error (Integral part), more overshoot the system will have. That is the reason why SGD-Momentum which accumulates past gradients will overshoot its target and spend more time during training.

和分别是系统的阻尼比和固有频率。在图3中，我们展示了权重的演化过程，作为的一个例子。从Eq(13)中，我们有。我们可以看到，是的单调递减函数，参考了Eq(8)的超调定义，你可以看到是单调递减的。那么，是一种单调递增的超调函数。因此，更多的历史误差（不可分割的部分），系统将会有更多的超调。这就是为什么在过去的梯度中积累的SGD-Momentum会超过目标，在训练中花费更多的时间。

As can be observed from Eq. (12), the term  brings periodically oscillation change to the weight, which is no more than 1. The term  mainly controls the convergence rate. One should note the value of hyper-parameter  in calculating the derivate  . It is easy to observe that the larger the derivate, the earlier the training convergence we will reach. However, when gets too large, the system will be fragile. In practice, we set the hyper-parameter  based on the Ziegler-Nichols optimum setting rule [33],which is widely used by engineers in PID feedback control since its origin in 1940s.

从Eq(12)可以观察到，会周期性地对权重进行振荡，而权重不超过1。项主要控制收敛速度。我们应该注意到超参数在计算推导出的时的值。我们很容易观察到，微分的规模越大，我们就能越早地达到训练的收敛性。然而，当变得太大时，系统将会变得脆弱。在实践中，我们基于Ziegler-Nichols的最优设置规则建立了超参数，这是自20世纪40年代以来，工程师们在PID反馈控制中广泛使用的。

According to Ziegler-Nichols' rule, the ideal setup of should be one third of the oscillation period, which means , where  is the period of oscillation. From Eq. (12), we can get  . If we make a simplification that the  in Momentum is equal to 1, then .Combined with Eq. (13), will have a closed form solution:

根据Ziegler-Nichols的规则，的理想设置应该是振荡周期的三分之一，也就是，其中是振荡的周期。从Eq(12)中，我们可以得到。如果我们把的动量等于1，那么。和Eq(13)结合在一起，会有一个闭合形式的解。

In practice, we can start with this ideal setting of Kd and change it slightly when use different network models to train on different datasets.

在实践中，我们可以从的理想设置开始，当使用不同的网络模型在不同的数据集上进行训练时，可以稍微改变它。

 

5. Experimental Results

In this section, we first trained an MLP on the MNIST handwritten digit dataset in Section 5.2 to show the advantage of PID optimizer, and then trained CNNs on the CIFAR datasets in Section 5.3 to demonstrate that PID optimizer is competitive with SGD-Momentum in accuracy but with much faster training speed. To further validate our PID optimizer on a larger dataset, in Section 5.4 we performed experiments on the Tiny-Imagenet dataset [36]. The results showed that our PID optimizer can generalize to modern networks and datasets. It should be noted that except for the additional hyper-parameter which is set by Eq.(14),all the other hyper-parameters in our PID optimizer are set as the same as SGD-Momentum. The learning rate starts
from 0.01 and is divided by 10 when the error plateaus. The source code of our PID optimizer can be found at https://github.com/tensorboy/PIDOptimizer.

在本节中,我们首先在5.2节用MNIST手写数字数据集训练一个MLP来显示PID优化器的优点,然后在5.3节训练cnnCIFAR数据集来证明PID优化器在准确性与SGD-Momentum竞争,但训练速度快得多。为了在更大的数据集上进一步验证我们的PID优化器，在第4节中，我们在Tiny-Imagenet数据集上进行了实验。结果表明，我们的PID优化器可以推广到现代的网络和数据集。应该注意的是，除了由Eq(14)设置的额外的超参数之外，我们的PID优化器中的所有其他超参数都设置为与SGD-Momentum相同。学习速率从0.01开始，当误差平稳时，就除以10。我们的PID优化器的源代码可以在https://github.com/tensorboy/pidoptimizer中找到。

5.1. Dataset

MNIST dataset: The MNIST dataset [37] contains 60;000 training samples and 10;000 test samples of the handwritten digits from 0 to 9. The images are of 28×28 pixels and in grey level format.CIFAR Dataset: The CIFAR10 and CIFAR100 datasets [38] consist of 60;000 RGB color images of resolution 32×32, drawn from 10 and 100 classes, respectively, and both split into 50;000 training and 10;000 test images. For data augmentation, we performed horizontal flips and random crops on the original image padded by 4 pixels on each side.Tiny ImageNet Dataset: The Tiny-ImageNet [36] dataset has 200 classes. Each class has 500 training images, 50 validation images, and 50 test images. The Tiny-ImageNet is more difficult than the CIFAR datasets because more classes are involved, and the relevant objects to be classified often cover only a tiny subspace of the image.

MNIST数据集：MNIST的数据集37包含60 000个训练样本和10 000个从0到9的手写数字的测试样本。这些图像的分辨率为像素，采用灰度格式。CIFAR数据集：CIFAR10和CIFAR100数据集38由60万个RGB颜色图像组成，分辨率为，分别来自10和100个类，并分为50 000个训练和10 000个测试图像。对于数据增强，我们在原始图像上执行水平翻转和随机裁剪，每侧填充4个像素。小型的ImageNet数据集：Tiny-ImageNet 36数据集有200个类。每个类有500个训练图像，50个验证图像，和50个测试图像。Tiny-ImageNet比CIFAR数据集要困难得多，因为涉及到更多的类，并且要分类的相关对象通常只覆盖图像的一个子空间。

 

5.2. Results of MLP on MNIST dataset

We first trained a simple MLP network on the MNIST handwritten digit classification dataset using the proposed PID optimizer and compare it with SGD-Momentum [7].The MLP network is with ReLU nonlinearity and 1;000 hidden nodes in the hidden layer, followed by the softmax output layer on top. The training was on mini-batches with 128 images per batch for 20 epochs through the training set.We run the experiments for 10 times and reported the average results. The detailed training statistics by the two methods are illustrated in Figure 4, from which we can see that PID optimizer not only converges more quickly than SGDMomentum with lower loss and higher accuracy, but also has higher generalization ability on the validation dataset.On the test dataset, PID optimizer achieves 98% accuracy and SGD-Momentum achieves an accuracy of 97:5%.

我们首先使用建议的PID优化器在MNIST的手写数字分类数据集上训练了一个简单的MLP网络，并将其与SGD-Momentum进行比较。MLP网络用ReLU的非线性（激活）和隐藏层中有1 000个隐藏节点，后面是softmax的输出层。通过训练，每批训练有128张图片，共有20个epoch。我们进行了10次实验，并报告了平均结果。这两种方法的详细训练统计数据如图4所示，从中我们可以看到，PID优化器不仅比SGD-Momentum更快速收敛，而且具有更低的损耗和更高的精度，而且在验证数据集上具有更高的泛化能力。在测试数据集上，PID优化器达到98%的准确率，SGD-Momentum达到97:5%。

图4。MNIST数据集的PID与SGD-Momentum跑20个epoch。最上面一行：训练损失和验证损失的曲线。下面一行：训练精度和验证精度的曲线。

图5。使用DenseNet 190-40，在CIFAR10数据集上的PID与SGD-Momentum。最上面一行：训练损失和验证损失的曲线。下面一行：训练精度和验证精度的曲线。

 

5.3. Results on CIFAR datasets

We then compared PID and SGD-Momentum optimizers on CIFAR10 and CIFAR100 by using five state-of-the-art CNN models, including ResNet [13], PreActResNet [23],ResNeXt29 [35], WRN [24], and DenseNet [14]. The results are summarized in Table1. The second column lists the number of depth of those networks, while the third column lists the number of parameters for each network model.The fourth column indicates the number of runs to calculate the average test error. In the fifth and sixth columns of Table 1, we presented the average test errors on CIFAR10 and showed the numbers of Epochs by PID and SGD-Momentum when they achieve the reported test errors for the first time (i.e., the least number of Epochs to reach the best accuracy). The last two columns of Table 1 present such comparisons on CIFAR100.

然后，我们用5个最先进的CNN模型，包括ResNet 、PreActResNet 、ResNeXt、WRN 和DenseNet，比较了CIFAR10和CIFAR100的PID和SGD-Momentum优化器。结果在表1中进行了总结。第二列列出了这些网络的深度，而第三列列出了每个网络模型的参数数量。第四列表示计算平均测试误差的运行次数。在表1的第五和第六列中，我们展示了CIFAR10上的平均测试误差，并在第一次实现报告的测试误差时显示了PID和SGD-Momentum的数量（例如最少数量的epoch达到最佳准确度）表1的最后两列显示了CIFAR100的这种比较。
From Table 1, we can have the following observations.First, our proposed PID optimizer achieves lower test errors than SGD-Momentum for all the used CNN architectures on both the two CIFAR datasets, except for ResNet with depth 1202. Second, PID optimizer converges faster (with less Epochs) than SGD-Momentum to reach the best results.In particular, our PID optimizer has on average 35% and up to 50% acceleration compared with SGD-Momentum.This demonstrates the importance of the change of gradient, which can be exploited to reduce the overshoot problem and speed up the learning process of DNNs. Figure 5 shows the detailed training statistics by the two methods on CIFAR10 with DenseNet 190-40 (190 layers with growth rate of 40) [14]. One can see that PID optimizer converges faster than SGD-Momentum with lower loss and higher accuracy。

从表1中，我们可以得到以下的观察结果。首先，我们所建议的PID优化器在两个CIFAR数据集上的所有使用的CNN架构的测试错误都要比SGD-Momentum低，除了深度为1202的ResNet。其次，PID优化器比SGD-Momentum收敛更快（更少的时间），以达到最好的结果。特别是，与SGD-Momentum相比，我们的PID优化器的加速平均为35%，最高为50%。这证明了梯度变化的重要性，可以利用它来减少超调问题，加快DNNs的学习过程。图5显示了CIFAR10的两种方法的详细训练统计数据，其中包括DenseNet 190-40（190层，增长率为40）14。我们可以看到，PID优化器的收敛速度快于SGD-Momentum，低损耗和更高精度

 

5.4. Experiments on Tiny-ImageNet

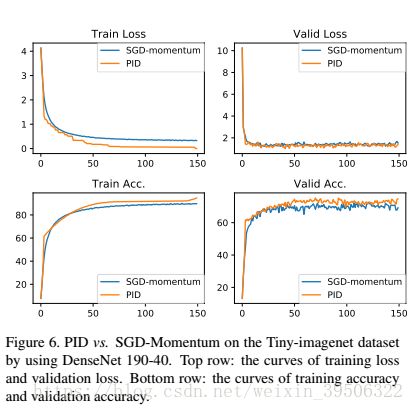
To further demonstrate the effectiveness of our PID optimizer, we employed the DenseNet190-40 architecture to perform experiments on the Tiny-ImageNet dataset. Figure 6 shows the curves of training loss and accuracy over Epochs, as well as the validation loss and accuracy by the PID and SGD-Momentum optimizers. The learning rate of SGD-Momentum and PID was fixed to 0:01. Training was conducted 150 epochs using batch size 64. The results are averaged over 5 runs.Similar conclusions to those on CIFAR datasets can be made. In both training and validation, PID converges faster than SGD-Momentum, has lower loss and achieves higher accuracy. Such results confirm the generalization capability of PID based DNN optimizer to large-scale datasets.

为了进一步演示我们的PID优化器的有效性，我们使用DenseNet190-40架构在Tiny-ImageNet数据集上执行实验。图6显示了训练损失和准确性的曲线，以及PID和SGD-Momentum优化器的验证损失和准确性。SGD-Momentum和PID的学习速率被固定为0.01。训练使用64的batch size，执行了150个epoch。每5次取一个平均结果。对CIFAR数据集也可以得出类似的结论。在训练和验证中，PID收敛速度快于SGD-Momentum，具有较低的损耗和更高的精度。这样的结果证实了基于PID的DNN优化器对大型数据集的泛化能力。

图6。通过使用DenseNet 190-40，在Tiny-imagenet数据集上的PID和SGD-Momentum。最上面一行：训练损失和验证损失的曲线。最下面一行：训练准确性和验证准确性的曲线 。

 

6. Conclusion

Inspired by the prominent success of PID controller in the field of automatic control, we investigated its connections with stochastic optimizers such as SGD and its variants, and presented a novel PID controller approach to deep network optimization. The proposed PID optimizer exploits the present, past and change information of gradients to update the network parameters, reducing greatly the overshoot problem of SGD-momentum and accelerating the learning process of DNNs. Our experiments on MINIST, CIFAR and Tiny-ImageNet datasets validated that the proposed PID optimizer is 30% ~ 50% faster than SGD-Momentum, whiling resulting in lower error rate. In future work, we will investigate how to adapt our PID optimizer to other network architectures such as LSTM and RNN, and how to associate PID optimizer with an adaptive learning rate for DNN optimization.
在自动控制领域中PID控制器的显著成功的启发下，研究了其与SGD等随机优化器的关系，并提出了一种新颖的PID控制器方法来进行深度网络优化。提出的PID优化器利用当前、过去和变化的梯度信息来更新网络参数，极大地减少了SGD-momentum的超调问题，并加速了DNNs的学习过程。我们在MINIST、CIFAR和Tiny-ImageNet数据集上的实验验证了，所建议的PID优化器比SGD-momentum快30%到50%，从而导致更低的误差率。在未来的工作中，我们将研究如何使我们的PID优化器适应其他网络架构，如LSTM和RNN，以及如何将PID优化器与自适应学习速率与DNN优化相关联。

 

References

[1] Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy,
Aditya Khosla, Michael S. Bernstein, Alexander C. Berg,and Fei fei Li. Imagenet large scale visual recognition challenge. IEEE International Journal of Computer Vision(IJCV), 2015. 1
[2] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems (NIPS), 2012. 1
[3] Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun.Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in neural information processing systems (NIPS), 2015. 1
[4] Florian Schroff, Dmitry Kalenichenko, and James Philbin.Facenet: A unified embedding for face recognition and clus-
tering. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015. 1
[5] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep Learning. MIT Press, 2016. 1
[6] Leon Bottou. Online learning in neural networks. chapter ´Online Learning and Stochastic Approximations, pages 9–
42. Cambridge University Press, 1998. 1, 2
[7] Ilya Sutskever, James Martens, George Dahl, and Geoffrey Hinton. On the importance of initialization and momentum
in deep learning. In International conference on machine learning, 2013. 1, 2, 7
[8] John Duchi, Elad Hazan, and Yoram Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research,12(Jul):2121–2159, 2011. 1, 2
[9] Geoffrey Hinton, N Srivastava, and Kevin Swersky. Lecture 6a overview of mini–batch gradient descent. 1, 2
[10] Diederik Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In International Conference for Learning Representations (ICLR), 2014. 1, 2
[11] Ashia C Wilson, Rebecca Roelofs, Mitchell Stern, Nati Srebro, and Benjamin Recht. The marginal value of adaptive gradient methods in machine learning. In Advances in Neural Information Processing Systems (NIPS), 2017. 1
[12] Daniel Jiwoong Im, Michael Tao, and Kristin Branson. An empirical analysis of the optimization of deep network loss
surfaces. In International Conference for Learning Representations (ICLR), 2017. 1
[13] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun.Deep residual learning for image recognition. In IEEE
Conference on Computer Vision and Pattern Recognition (CVPR), 2016. 1, 2, 7, 8
[14] Gao Huang, Zhuang Liu, Laurens van der Maaten, and Kilian Q Weinberger. Densely connected convolutional networks. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017. 1, 2, 7, 8
[15] Katsuhiko Ogata. Discrete-time control systems, volume 2.Prentice Hall Englewood Cliffs, NJ, 1995. 1, 5
[16] Laurent Lessard, Benjamin Recht, and Andrew Packard.Analysis and design of optimization algorithms via integral quadratic constraints. SIAM Journal on Optimization,26(1):57–95, 2016. 2
[17] L. Wang, T. J. D. Barnes, and W. R. Cluett. New frequencydomain design method for pid controllers. IEEE Control Theory and Applications, Jul 1995. 2
[18] Kiam Heong Ang, G Chong, and Yun Li. Pid control system analysis, design, and technology. 13:559 – 576, 08 2005. 2,3
 [19] Pan Zhao, Jiajia Chen, Yan Song, Xiang Tao, Tiejuan Xu,and Tao Mei. Design of a control system for an autonomous vehicle based on adaptive-pid. International Journal of Advanced Robotic Systems, 9(2):44, 2012. 2
[20] A. L. Salih, M. Moghavvemi, H. A. F. Mohamed, and K. S.Gaeid. Modelling and pid controller design for a quadrotor unmanned air vehicle. In IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), volume 1, pages 1–5, May 2010. 2
[21] Paolo Rocco. Stability of pid control for industrial robot arms. IEEE transactions on robotics and automation, 1996.2
[22] Pierre Simon de Laplace. Theorie analytique des proba- ´bilites ´ , volume 7. Courcier, 1820. 2, 5
[23] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun.Identity mappings in deep residual networks. In IEEE European Conference on Computer Vision (ECCV), 2016. 2, 7,8
[24] Sergey Zagoruyko and Nikos Komodakis. Wide residual networks. In BMVC, 2016. 2, 7, 8
[25] Yurii Nesterov. A method of solving a convex programming problem with convergence rate o (1/k2). In Soviet Mathematics Doklady, 1983. 2
[26] Weijie Su, Stephen Boyd, and Emmanuel Candes. A differential equation for modeling nesterov0s accelerated gradient method: Theory and insights. In Advances in Neural Information Processing Systems (NIPS), 2014. 2
[27] J Clerk Maxwell. On governors. Proceedings of the Royal Society of London, 16:270–283, 1867. 3
[28] Nicolas Minorsky. Directional stability of automatically steered bodies. Journal of ASNE, 1922. 3
[29] Emre Sariyildiz, Haoyong Yu, and Kouhei Ohnishi. A practical tuning method for the robust pid controller with velocity feed-back. Machines, 3(3):208–222, 2015. 3
[30] David E Rumelhart, Geoffrey E Hinton, and Ronald J Williams. Learning representations by back-propagating errors. Nature, 1986. 3
[31] Murray R Spiegel. Advanced mathematics. McGraw-Hill,Incorporated, 1991. 4
[32] KA DE JONG. An analysis of the behavior of a class of genetic adaptive systems. Doctoral Dissertation, University of Michigan, 1975. 5
[33] John G Ziegler and Nathaniel B Nichols. Optimum settings for automatic controllers. trans. ASME, 64(11), 1942. 5, 6
[34] George E Robert and Hyman Kaufman. Table of Laplace transforms. Saunders, 1966. 5
[35] Saining Xie, Ross Girshick, Piotr Dollar, Zhuowen Tu, and ´Kaiming He. Aggregated residual transformations for deep neural networks. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017. 7, 8
[36] Ya Le and Xuan Yang. Tiny imagenet visual recognition challenge. 2015. 6, 7
[37] Yann LeCun, Leon Bottou, Yoshua Bengio, and Patrick ´Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.7
[38] Alex Krizhevsky. Learning multiple layers of features from tiny images. 2009. 7
 

论文网址：

http://www4.comp.polyu.edu.hk/~cslzhang/paper/CVPR18_PID.pdf

GitHub网址：

https://github.com/tensorboy/PIDOptimizer