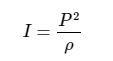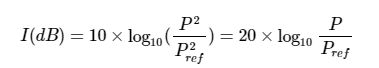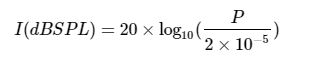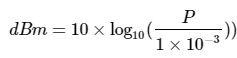关于音频标准化以及dB的理解

名词解析

dB 本质是比值

分贝dB定义为两个数值的对数比率，这两个数值分别是测量值和参考值（也称为基准值）, 它和很多常见的单位如“米”，“秒”或者“千克”等物理单位是不同的，它并不能直接用来描述一个物理量的大小或者多少，它表示的是两个相同单位物理量的比值。作为分母的那个量通常是一个标准的基准值（standard reference value），分贝描述的就是作为分子的物理量相对于这个基准值的大小，分贝的计算公式如下：

其中，$valu{e}_{ref}$ 是基准值。在使用分贝表示物理量基准值是非常重要的，基准值用分贝表示的话是0dB。它是个无量纲， 因为是比值嘛

有很多物理量的比值可以得到分贝

dB(dBSPL)

声学领域，dB经常用作为表征声压级SPL（Sound Pressure Level）的大小，声音本质上来说是一种波，通过空气传播，传到人耳朵里引发鼓膜的振动。所以，声音的大小，实际就是对这种振动强度的反映。而由于空气的振动会引起大气压强的变换，可以使用**压强变化的程度来描述声音的大小，这就是“声压(SPL,Sound Pressure Levels)”概念，其单位是Pa。**例如：1米外步枪射击的声音大约是7000Pa；10米外开过汽车大约是0.2Pa。

使用声压作为测量量的分贝就是dBSPL，通常用来表示声音大小的dB多说指的就是dBSPL。声压和声音大小的关系，可以使用如下公式表示

其中，I是声音的强度；P是声压；ρ是空气阻力，通常在室温下，空气阻力大约是400。

分贝的计算还需要一个 选择一个特定的声压值作为“标准值”（0分贝），该值是固定的. 有了这个基准值后代入上面的公式:

这里选择的声压标准值为 $2\times 10-5Pa,20\mu Pa$，是人耳在1KHz这个频率下能听到的最小的声音，大致相当于3米外一只蚊子在飞的声音。将标准值代入上式：

dBm,dBu,dBV

前面根据声音的振动，在传播的过程引起大气压强的变化，使用声压作为测量量来计算声音的分贝值。除了自然产生的声音外，现在大多数的声音都是使用电信号作为存储和传播的载体的，例如电视广播，各种音频文件等。dBm,dBu,dBV是使用和电信号相关的物理量作为被测物理量，计算其产生声音的分贝值。

dBm

dBm是使用产生声音信号的功率作为被测物理量，选择1毫瓦(1mW)作为基准值，计算分贝值。计算公式:

功率P可以由电压V和电阻R计算得到 $$P=\frac{V^2}{R}$$

dBu

由上面的公式可以得到 dBu, 即使用电压作为测量量，计算声音的分贝值。在十九世纪三十年代，音频设备的输入电阻都是600欧姆，也就上面公式中的R=600欧姆。在dBm中，使用1mW作为基准值，那么在R=600欧姆时就可以得到此时的电压为0.775V。所以，dBu是以电压作为测量量，计算声音的分贝值，选择的基准电压为0.775V。计算公式：

$$dBu=20\times {\log }_{10}(\frac{V}{0.775})$$

dBV

上世纪实际音频设备的输入阻抗都是600欧姆，是固定不变的。但是到了现代，就有了更高阻抗的设备，例如1000欧姆，这样再选择0.775作为电压的基准值，显然是不合理的。所以，就有了一个新基准值1V。本质上dBu和dBV是没有区别的，都是选择电压作为被测单位，只是选择的基准值不同罢了。dBV仍然是以电压作为被测量，计算声音的分贝值，选择1V作为基准值。计算公式：

$$dBV=20\times {\log }_{10}(\frac{V}{1})$$

dBFS

前面的几个被测量都是模拟量，在数字时代更多的音频分贝表示是dBFS。dBFS的全称为Decibels Full Scale，全分贝刻度，是数值音频分贝值的表示方法。和前面几个不一样的时，dBFS的基准并不是最小的或者是中间的某一个值，是最大的那个值！也就是说0dBFS是数字设备能达到的最大值，除了最大值外都是负值。
以数字音频的sample为16位无符号为例，16位的无符号的最大值为65536，因此dBFS的计算公式：

$$dBFS=20\times {\log }_{10}(\frac{sample}{65536})$$

这样，最小的dBFS = $20\times {\log }_{10}\frac{1}{65536}=-96dBFS$。也就是说16位无符号音频的动态范围为0 ~ -96dBFS。

dBFS 和 dBu之间的转换

dBu是度量模拟信号的，而dBFS是度量数字信号的，并且dBFS不会用于度量模拟信号，所以没有在dBu和dBFS之间没有统一的转换公式，依赖于具体的数字设备。在dBu和dBFS转换时，需要规定一个峰值电压，该电压下产生的音频信号经过AD转换后得到的sample为0dBFS。例如，+18dBu对应于0dBFS，在该条件下 求 xdBu对应于ydBFS，那么就有 $y=x-18$

总结

• dBSPL，通常所说的dB，使用声压作为被测量，选择$20\mu Pa$作为基准值。

• dBm，使用功率作为被测量，选择1mW作为基准值。

• dBu，使用电压作为被测量，选择0.775V作为基准值。

• dBV，和dBu一样，使用电压作为被测量，选择1V作为基准值。

• dBFS，和上面的量都不相同，上面的量都是测量模拟值的，dBFS是测量数字音频的，其选择的基准值为sample的最大值为0dBFS，其他的值都为负值。

• dBFS和模拟量之间的转换，例如dBu，需要规定一个基础的对应关系。例如+18dBu 对应于0dBFS，则ydBFS = x - 18。

标准化音频是什么？为什么这么做？

是什么

• 标准化音频就是change its overall volume by a fixed amount to reach a target level， 也就是让音量到一个固定的区间

• ideally does not change the sound in any way other than purely changing its volume. 理想情况下除了音量别的参数不会改变

为什么

1.得到更响的音频

比如你有一些声音很小的音频, 你想要让它的声音尽可能大(达到0dBFS), 但是不改变它的动态范围(dynamic range: 是可变化信号（例如声音或光）最大值和最小值的比值。也可以用以10为底的对数（分贝）或以2为底的对数表示。), 如下面的图:

2. 音量匹配

比如你有一组音频, 它们有不同的音量, 你可能想要它们的音量尽可能的接近,它不能影响与大部分声音相关的峰值。

怎样做

• 归一化之前比如先决定如何测量音频的响度, 然后再使用不同的方法

Peak volume detection

• 这种只考虑音频响度的最大值, 假如你想让音频尽可能响可以用这种方式去检测

RMS volume detection

• 这种会考虑整体音频的响度, 但是还是不够接近人耳, 因为人在不同的响度下会感知到不同的频率, 如果一个音频文件包含许多不同的频率, 它会听起来更响, RMS没有考虑这点, 于是有了下面的方法

EBU R 128 volume detection

这是一种类似于RMS测量音量的方法，但可以被认为是模拟人耳方法。它智能地聆听音量，并思考我们将如何听到它。它理解我们听到1000 - 6000 Hz之间的频率的音量更大，并考虑到了这一点。