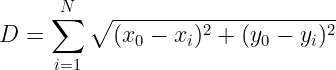模拟退火-n皇后问题

模拟退火 

这里只做快速了解，用来解决常见问题。

简单了解一下模拟退火：

模拟退火是模拟物理上退火方法，通过N次迭代（退火），逼近函数的上的一个最值（最大或者最小值）。

模拟退火可行性：

我们想象一个固体放在那里，如果该固体温度此时很高，运用我们高中的知识，此时该物体的内能较大，因为其内部无规则运动的粒子动能较大，分子热运动较快。 此时看作一个十分无序的状态，当其慢慢降温，随着温度降低到正常室温，其内部的粒子慢慢‘有序’ ，此时较为稳定。

注意文字中的内容：

1. 温度高--运动速度快，温度低--运动速度慢。
2. 温度缓慢降低。
3. 温度恢复到正常室温后趋于有序(接近最优解)。

因此，模拟退火的大方向为：

模拟退火就是一种循环算法。

1. 我们先设定一个初始的温度T（这个温度要比较高，比如2000）
2. 每次循环都退火一次。（具体怎么操作后面详解）
3. 然后降低T的温度，我们通过让T和一个“降温系数”ΔT（一个接近1的小数，比如0.990.99)相乘，达到慢慢降低温度的效果，直到接近于0（我们用eps来代表一个接近0的数(比如0.00001)，只要T

简易代码如下：

T = 2000  # 代表开始的温度
dT = 0.99  # 代表系数delta T
eps = 1e-14  # 相当于0.0000000000000001
while T > eps:
    '''
    这里是每一次退火的操作
    '''
    T = T * dT  # 温度每次下降一点点， T * 0.99

以下面函数为例：

如  

我们要求解的答案无非是两个：自变量xx和对应函数的最大值f(x)

1. 随机找一点x0(定义域内随机)，并获取了该点对应的f(x0).

 

2. 开始退火

像前面所讲x0相当于一个粒子，所以我们会进行一个无序运动，也就是向左或者向右随机移动。

但是请记住一个关键点：移动的幅度和当前的温度T有关。

温度T越大，移动的幅度越大。温度T越小，移动的幅度就越小。这是在模拟粒子无序运动的状态。

 

3. 接受更好的状态

上图中我们移动到了x2处，明显f(x2)优于f(x0)。

因此我们将答案进行更新: x0=x2,f(x0)=f(x2), 这也是一种贪心的思想。

 

4. 以一定概率接受更差的状态

这也是退火最精彩的部分。

为什么我们要接受一个更加差的状态呢？因为可能在一个较差的状态旁边会出现一个更加高的山峰。

如果我们一开始只注重了x0最开始随机的那一点区域(图像左侧)，随着温度的下降、左右跳转幅度的减小，我们终将受困于此，仅得到局部最优的答案。

 

而我们如果找到了右边山峰的低点，以一定的概率接受了它（概率大小和温度以及当前的值的关键程度有关），会在跳转幅度减少之前，尽可能找到最优点。

那么我们以多少的概率去接受它呢？我们用一个公式表示（这个公式我们只需记住，这是科学家推导而来）：

分别讲解下各部分含义： 

 ：因为我们用函数来代表一个概率值，所以我们只需要关注x为负数的部分即可： 

负数部分的值域是在(0,1)开区间内，x越小，越接近0，越大越靠近1。

因为在0到1之间，所以这个值相当于是概率了。比如=0.97，那么我们接受的概率就是97%，

而正数部分的值域会大于1，也就是说概率会超过100%，所以一定会选（其实是上一种找到更优的情况）

k：其实是个物理学常数，我们在代码中不会用到。

T：很简单，就是当前的温度。所以实际上这个分母就是T，k当做1使用。

Δf：下面着重讲一下什么是Δf。

其实从前面的函数中可以发现，Δf必须是个负数。

Δf就是当前解的函数值与目标解函数值之差，Δf=−|f(x0)−f(x1)|，并且一定是个负数。

比如现在我们求一个函数的最大值，那么如果f(x0)变好了(具体问题具体分析)，我们肯定选择它（见第3点：接受更好的状态）。

如果f(x0)>f(x1)，那就说明结果变差了，我们需要概率选择它，因此Δf=−(f(x0)−f(x1))。

 

我们可以用  与(0,1)之间生成的随机数做比较，大于则接受反之则不接受

 

ps: 不难看出温度越高时，接受的概率就越大。Δf越小，说明答案越糟糕(f(x1)与f(x2)相差很多，但也要概率接受)，那么接受的概率就越小。

 

所以总结一下就是：

• 随机后的函数值如果结果更好，我们一定选择它(即x0=x1,f(x0)=f(x1))
• 随机后的函数值如果结果更差，我们以的概率接受它

 

例题1：通过模拟退火算出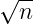的值

我们通过函数f(x)中x的跳动去寻找结果。不妨设：

import math
import random


# x表示我们随机产生的那个数的平方和n的靠近程度
def func(x, n):
    return abs(x * x - n)


# 模拟退火
def SA(T, dT, eps, n):
    # 根号10大约为3.1622 这里人为限制范围 也可以直接随机 反正后面要受温度影响来回跳动且是随机的
    x = random.uniform(1.6, 5.4)
    # 算出x平方和n的差距f(x0)
    f = func(x, n)
    while T > eps:
        # 根号下的数一定是非负的 所以可以直接随机非负数
        new_x = random.randint(-13, 20) * T # 温度影响来回跳动且是随机无规则的 这里随意限制了下范围
        new_f = func(new_x, n)
        if new_f < f:
            x = new_x  # 替换 如果多个变量就替换多个
            f = new_f
        elif math.exp((f - new_f) / T) > random.random():  # 概率接受 ex在(0,1)之间 实际上random.random()在[0,1)
            x = new_x
            f = new_f
        # 降温
        T *= dT
    # 输出结果 近似值 如我本次是 3.1201885471764994
    print(x)


if __name__ == '__main__':
    n = 10  # n代表我们最后函数要逼近的值
    T = 20000  # 初始温度，初始温度主要是看题目开始需要跳转的幅度。
    dT = 0.993  # 变化率，这里需要速度稍微慢一点，写0.995 或者 0.997都可以，但是越靠近1速度就越慢
    eps = 1e-14  # 10的-14次方已经非常小了，写这个大概率没问题

    SA(T, dT, eps, n)

例题2：点距之和最小

给出平面上N（N<=100）个点，你需要找到一个这样的点，使得这个点到N个点的距离之和尽可能小。输出这个最小的距离和（四舍五入到最近的整数）。

Input输入

第一行N，接下来N行每行两个整数，表示N个点

4
0 0
0 10000
10000 10000
10000 0

Output输出

一行一个正整数，最小的距离和。

28284

们的函数func()就是：求出一个随机点A=(x0,y0)到NN个点的距离之和DD，就是把这个点A和所有N个点的距离相加，即：

n皇后问题

简单来说就是一个n*n的棋盘中，每一行只落一枚棋，且该棋所在的列、左斜线、右斜线均无其它棋子。

import copy
import random
import time
import math
import numpy as np


def init():
    cache = {}
    m = np.zeros((8, 8), dtype=int)
    for i in range(0, 8):
        temp = random.randrange(0, 8)
        m[temp, i] = 1
        cache["queen" + str(i)] = [temp, i]
    return m, cache


# 计算当前状态无碰撞数量
def compute_weight(coord_cache):
    weight = 0
    for i in range(0, 8):
        x, y = coord_cache["queen" + str(i)]
        for j in range(i + 1, 8):
            x2, y2 = coord_cache["queen" + str(j)]
            if x2 - x == j - i or x2 - x == i - j:
                weight += 1
            if x2 == x:
                weight += 1
    return 28 - weight


# 随机生成一个新的解
def random_adjust(coord_cache):
    temp = copy.deepcopy(coord_cache)
    row = random.randrange(0, 8)
    column = random.randrange(0, 8)
    temp["queen" + str(column)] = [row, column]  # 调整皇后的位置
    return temp


def draw(coord_cache):
    m = np.zeros((8, 8), dtype=int)
    for i in range(8):
        row, column = coord_cache["queen" + str(i)]
        row, column = int(row), int(column)
        m[row][column] = 1
    return m


def cool(T, eps, dt, L):
    m, coord_cache = init()
    print("初始化八皇后状态为：\n", m)
    while T > eps:  # 温度循环
        for i in range(L):  # 每个温度循环L次
            weight = compute_weight(coord_cache)
            print("当前状态的无碰撞度为：", weight)
            if weight == 28:  # 非碰撞度为28，表明找到了最优解
                return True
            new_coord_cache = random_adjust(coord_cache)  # 随机调整得到一个新的解
            new_weight = compute_weight(new_coord_cache)  # 计算新解的碰撞度
            print("随机调整产生的新解为：\n", draw(new_coord_cache))
            print("随机调整产生的新解的无碰撞度为：", new_weight)
            if new_weight >= weight:  # 新的解碰撞度更小就就收这个解
                coord_cache = new_coord_cache
                print("这是一个更好的解，直接接收：\n", draw(coord_cache))
            else:
                if random.random() < math.exp((new_weight - weight) / T):  # 否则就已模拟退火的概率接受作为新的解
                    coord_cache = new_coord_cache
                    print("当前的接收概率为：", math.exp((new_weight - weight) / T))
                    print("这是一个更差的解，但被接收了：\n", draw(coord_cache))

        T = T * dt


def Cool(T, eps, dt, L, num):
    t1 = time.time()
    success = 0
    fail = 0
    for i in range(num):
        if cool(T, eps, dt, L):
            success += 1
            print("第{0}个例子找到最优解".format(i))
        else:
            fail += 1
            print("第{0}个例子失败".format(i))
    t2 = time.time()
    print("{}个例子中成功解决的例子为：{}".format(num, success))
    print("{}个例子成功解决的百分比为：{}".format(num, success / num))
    print("{}个例子中失败的例子为：{}".format(num, fail))
    print("{}个例子失败的百分比为：{}".format(num, fail / num))
    print("{}个例子运行算法所需的时间为：{}秒".format(num, t2 - t1))


Cool(5, 0.001, 0.98, 150, 1000)

n皇后其它解法：

位运算(这里只输出一种可行解)：

def draw(n, ini):
    for i in ini:
        print('+---' * n + '+', end='')
        print('')
        print('| ' + ' | '.join(['#' if j == '0' else 'Q' for j in list(i[2:].rjust(n, '0'))]) + ' | ')
    print('+---' * n + '+', end='')


def DFS(row, colomn, left, right):
    global ini
    global result
    global flage
    bits = ((1 << n) - 1) & ~(colomn | left | right)  # 当前行可用列
    if bits == 0 and len(ini) != 0:
        ini.pop()
    while bits:
        pos = bits & -bits  # 获取该行列的位置
        bits = bits & (bits - 1)  # bits ^= pos
        if row == n - 1:
            result += 1
            if flage:
                ini.append(bin(pos))
                draw(n,ini)
                flage-=1
        else:
            if flage:
                ini.append(bin(pos))
            DFS(row + 1, colomn | pos, (left | pos) >> 1, (right | pos) << 1)
            if bits == 0 and len(ini) != 0:
                ini.pop()

n = 6
result = 0
flage = 1  # 用来保留单一解
ini = []
DFS(0, 0, 0, 0)
print('\n','{}种情况'.format(result))

另一种数学思想：

# 判断点[row, col]是否可以放置皇后
def check(matrix, row, col):
    for i in range(row):
        if abs(matrix[i] - col) == 0 or abs(matrix[i] - col) == abs(row - i):
            return False
    return True


def queen(matrix, row):
    global result
    n = len(matrix)
    if row == n:
        for col in matrix:
            print(' # ' * col + ' Q ' + ' # ' * (n - (col + 1)))
        print('')
        result += 1
    for col in range(n):
        if check(matrix, row, col):
            matrix[row] = col
            queen(matrix, row + 1)


n = 10
result = 0
matrix = [0] * n
queen(matrix, 0)
print('共有{}种结果'.format(result))