随机森林原始论文_SMAC: 基于随机森林的贝叶斯优化

贝叶斯优化中，除了代理模型(surrogate model)为高斯过程外，另一种用得比较多的代理模型为随机森林，本文将详述基于随机森林的贝叶斯优化：SMAC；并且介绍一个贝叶斯优化的开源包: Scikit-Optimizer(skopt)

一. SMAC: 基于随机森林的贝叶斯优化

1. 问题描述

传统的基于高斯过程的贝叶斯优化只能处理参数空间为连续or数值类型的变量，但是在机器学习中，有大量的参数类型为离散，或者参数之间是条件关系的情况；

比如在SVM中，关于核函数的选取，在scikit-learn中支持linear, polynomial, rbf, sigmoid四种类型，那核函数这个参数就是一个离散的参数；

又比如，假设当前有一个模型参数，我们关心两类模型，线性回归和Lasso回归，那该模型参数就是一个离散类型，假如模型参数为Lasso回归，而我们知道Lasso回归有一个参数是λ，那也就是说λ这个参数与模型参数是有着条件关系，当模型选择Lasso时，λ参数才会被激活(active)；

大多数研究通过巧妙的改造高斯过程的核函数从而使得该方法能够支持离散或者条件的空间, 但是都很难让大家信服这些方法；

因此，关于代理模型替换的研究就涌现，常见有基于随机森林的SMAC, 与Tree-structured Parzen Estimator（TPE）两种方法，今天，我给大家讲述基于随机森林的SMAC算法的思想；

2. SMAC

step1: 背景引入

SMAC全称Sequential Model-Based Optimization forGeneral Algorithm Configuration，算法在2011被Hutter等人提出。该算法的提出即解决高斯回归过程中参数类型不能为离散的情况

step2: 随机森林建模

假设当前我们已有一些初始样本点{(x_1, f(x_1)), (x_2, f(x_2)), ..., (x_n, f(x_n))}；【注：在AutoML优化中，这里的x_n不是数据集中的样本数据，而是模型以及模型超参数，而f(x_n)是在该模型超参数配置下，在某个固定的数据集上的表现，这在上篇文章中也强调过！】，然后根据这些点，我们建立一个随机森林模型去拟合f；该过程可以类比高斯回归过程中n个点所构成的多维正态分布；
由于随机森林可以处理离散变量，因此该方法很自然地使用与变量类型为离散情况，而对于条件限制情况，只需要在参数空间中加入条件限制，保证一些不可能的情况不会被采样到即可；

在原论文中，每颗树分裂时随机选择特征比例为5/6, 叶节点需要的最少数据数量为10，树的数量也为10；

step3 均值与方差：每颗树为一个预测结果

在高斯回归过程中，对于新加入的点x与之前的点构成新的多维正态分布，然后求解新加入点的边际分布即可得到新加入的点的均值与标准差，那么在随机森林的模型又是如何做到的呢？对于新加入的点x，在随机森林的每个树上有一个预测结果，把所有树的预测结果求平均即得到均值，预测结果求标准差即为标准差；

随机森林的另外一个好处就是对于某个点x, 其在每颗树上的预测复杂度只有O(logN)，而在高斯回归过程中，需要进行复杂的矩阵相乘才可以得到均值与标准差】

step4 下一次迭代点选取：大规模随机采样

正因为随机森林对于需要探索的点x的预测复杂度不高，因此关于候选点x的选取，在SMAC原论文中通过大规模采样得到；具体的：

在当前数据点中选取使得acquisition function最大的10个点作为起点，通过random neighbors方法找到邻居点，并带入随机森林模型进行预测；某个点的random neighbors的定义：该点所有的离散变量的取值随机切换，该点所有连续变量以当前取值为均值,0.2为标准差采样切换(连续变量事前被normalize到[0,1] )；通过该方法随机采样10000个点，带入随机森林预测均值与标准差，然后计算acquisition function，并选取最大的点作为下一个迭代点；

3. 算法

二. Scikit-Optimizer

1.介绍

当前Python中关于SMAC相关算法的开源库有smac3, Scikit-Optimizer, nni, autogluon。

其中smac3是提出smac算法的作者的团队开发的包，而算法实现也基本参考原论文，autosklearn也是基于该包基础上开发，但由于smac3在笔者的macOS系统上安装一直有问题，且在服务器上跑也有一些版本问题，因此笔者并未尝试该包；

nni是微软的automl的一个开源框架，支持的算法非常多，smac也是其中一个，nni中的smac是在smac3包上wrapper了一下；

autogluon是亚马逊的一个开源框架，亚马逊的principal scientist李沐说autogluon在detection模型上非常厉害，可以吊打很多工程师，而autogluon在贝叶斯优化算法这一块，是基于Scikit-Optimizer上封装；

Scikit-Optimizer( skopt )是在numpy, scipy与scikit-learn包基础上进行开发的，官方文档在这里：https://scikit-optimize.github.io/stable/index.html

下面我讲解下该包并为大家提供一个code example;

2. 概率建模支持

skopt有四种搜索优化方式：

a) dummy_minimize: 随机搜索
b) forest_minimize: 基于随机森林Ensemble Tree的贝叶斯优化
c) gbrt_minimize: 基于gradient boosting的贝叶斯优化
d) gp_minimize: 基于高斯回归过程的贝叶斯优化

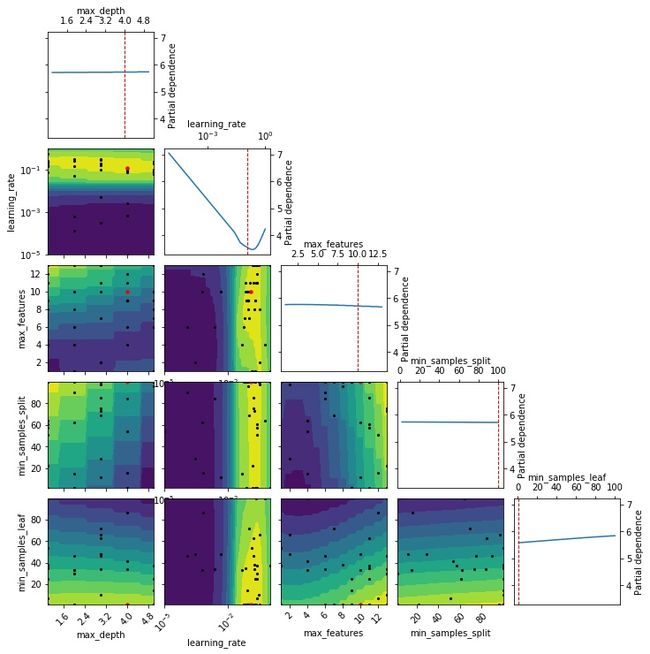
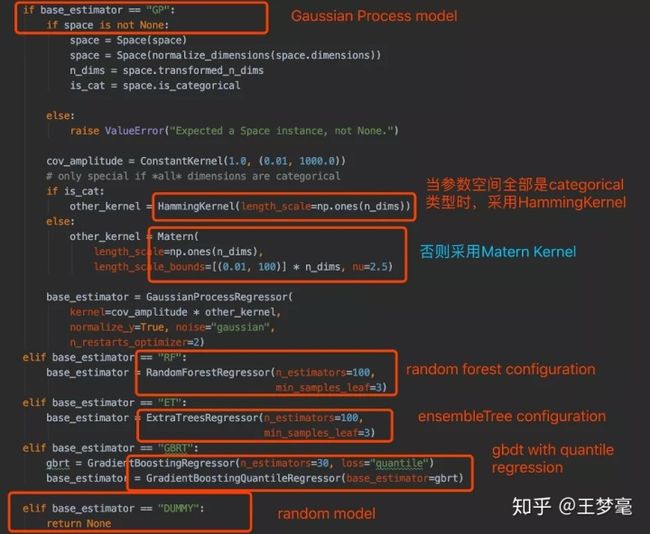
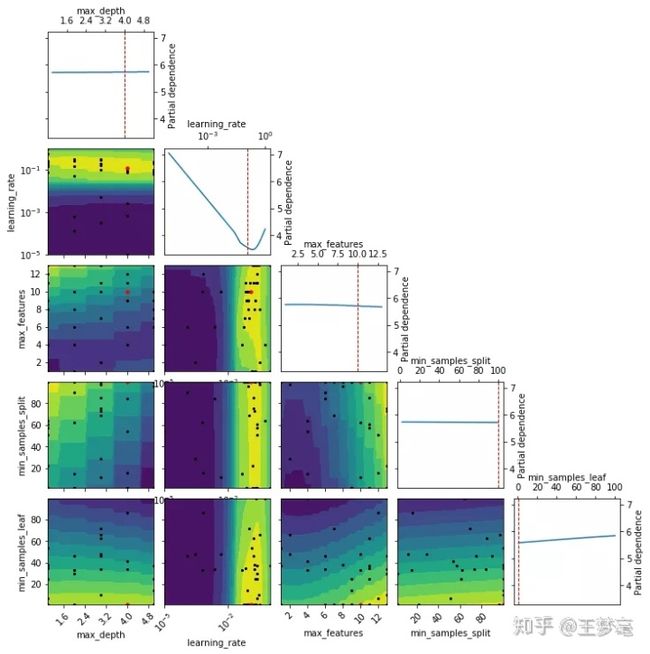
上图是skopt源码关于这四种搜索方式的具体实现。
对于高斯回归过程，如果参数空间不全是categorical类型的话，就是Matern Kernel ，如果全是categorical类型的话，就是Hamming Kernel(之后有时间可以介绍下这两个kernel);

对于SMAC，基于随机森林与基于ensemble_tree的情况下框默认用n_estimators=100, min_sample_leaf=3；
对于基于gbdt的情况，是用的分位数loss；

而DUMMY对应随机搜索, 则不对应任何模型;
最外层的导入接口如下：其中ensembleTree 与RandomForest在forest_minimize中被设定

3. 参数空间定义

skopt中支持三种基础的参数类型，Real, Int, Categorical三种，分别对应float, int, categorical类型的变量。其中float与int有normalize方法把原输入空间映射到某个bound中(比如[0,1]), categorical类型有onehot, label,string三种编码方式；

上图为一个例子说明，比如我们想优化GradientBoostingRegressor模型的相关参数，其中感兴趣的参数包括max_depth, learning_rate, min_samples_split, min_samples_leaf以及loss类型；那么只需要通过如上方法，指明一个范围，但必须保证name与GradientBoostingRegressor的字段参数对应；

4. 目标函数

关于目标函数，只需要通过skopt自带的一个decorator: use_named_args传入之前定义好的space，并定义objective函数即可，上图展示的某回归数据集下，五折交叉验证的neg_mean_absolute_error作为目标函数；

5. 运行模型

接下来，只需要把参数空间，目标函数带入我们模型即可，上图是带入到基于高斯回归过程建模的一个例子，其中关于xxx_minimize函数中，相关控制参数非常多，下面说一下最重要的几个参数

1) n_calls: int; 迭代次数，default=100
2) n_random_starts: int; 迭代开始前，先随机初始化的点的数量，default=10；
3) acq_func: str; 即采集函数acquisition function; 支持"LCB","EI", "PI", "EIps", "PIps", 关于这几种采集函数的具体定义，之后有时间我再来谈谈；
4) n_points: 在skopt中，并不是采用smac原论文的采样候选点的方式，而是随机采样，n_points即控制随机采样的点数，default=10000；

三. 总结

1. 本文简要讲述了基于随机森林的贝叶斯优化SMAC，SMAC的引入是为了解决基于GP只能解决数值类型的问题，在skopt中我们也看到该开源库也未能很好地解决该问题；

由于随机森林的训练与预测时间复杂度较低，因此在SMAC中可以轻易采样候选点，因此SMAC对真实函数有噪音的情况会更加robust一点；实验表明，当参数空间较复杂且维度较大时，采用SMAC效果会更优一点；

2. skopt实现了当前主流的一些贝叶斯优化方法，且非常容易上手，但细看源代码的话，也能看出skopt在一些细节上处理的问题；但不管怎么说，是一个非常好用的工具；

四. 参考文献

Hutter F., Kotthoff L., Vanschoren J.: Automated Machine Learning, p. 9 – 13. The Springer Series on Challenges in Machine Learning

Shahriari, B., Swersky, K., Wang, Z., Adams, R., de Freitas, N.: Taking the human out of the loop: A review of Bayesian optimization. Proceedings of the IEEE 104(1), 148–175 (2016)

Frank Hutter, Holger Hoos, and Kevin Leyton-Brown.
Sequential Model-Based Optimization for General Algorithm Configuration In LION-5, 2011.

这里是 梦毫学习笔记 的第二篇文章，欢迎与各位知乎大佬们共同交流讨论提高；也欢迎感兴趣的朋友们关注我的微信公众号：

http://weixin.qq.com/r/PDhTS9nEvYTCrZ0o920u (二维码自动识别)