数学建模——评价模型之TOPSIS
文章目录
- 一、TOPSIS的应用场景
- 二、TOPSIS法的模型建立
-
- 1.对原始决策矩阵正向化
- 2.决策矩阵标准化
- 3.计算得分并归一化
- 三、TOPSIS与(组合)赋权法结合
- 代码
一、TOPSIS的应用场景
Topsis法,全称为Technique for Order Preference by Similarity to an Ideal Solution,中文常翻译为优劣解距离法,该方法能够根据现有的数据,对个体进行评价排序。根据有限个评价对象与理想化目标的接近程度进行排序的方法,是在现有的对象中进行相对优劣的评价。
下图中假设只有两个评价指标,因此是二维坐标。
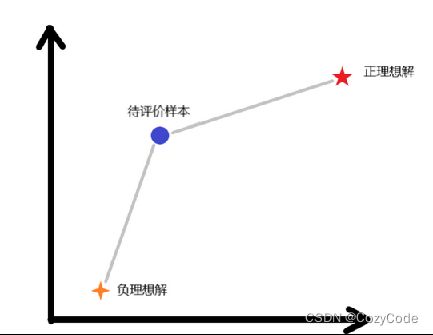
TOPSIS法其中“理想解”和“负理想解”是TOPSIS法的两个基本概念。
- 所谓理想解是一设想的最优的解(方案),它的各个属性值都达到各备选方案中的最好的值
- 负理想解是一设想的最劣的解(方案),它的各个属性值都达到各备选方案中的最坏的值。
二、TOPSIS法的模型建立
主要步骤:
- 原始决策矩阵正向化
- 决策矩阵标准化
- 计算得分并归一化
1.对原始决策矩阵正向化
构造决策矩阵 A = ( a i j ) m × n A=\left(a_{i j}\right)_{m \times n} A=(aij)m×n,每一列是一个评价指标,每一行是一条待评价样本。
有的数据是越大越好,有的数据是靠近某个值越好,有的是在一个区间中最好,这种不同的方向和区间让分析变得混乱,为了简化分析我们将数据进行正向化处理,都让他越大越好。
最常见的四种指标:
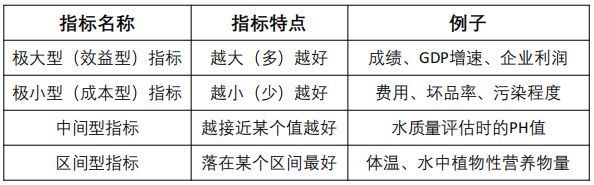
所谓的将原始矩阵正向化,就是要将所有的指标类型统一转化为
极大型指标。
- 极小型指标转化为极大型指标:
使用公式
max − x \max -x max−x
如果所有的元素均为正数,那么也可以使用 1 x \dfrac{1}{x} x1 - 中间型指标转化为极大型指标:
x ˉ i = 1 − ∣ x i − x best ∣ max ( ∣ X − x best ∣ ) \bar{x}_{i}=1-\frac{\left|x_{i}-x_{\text {best }}\right|}{\max \left(\left|X-x_{\text {best }}\right|\right)} xˉi=1−max(∣X−xbest ∣)∣xi−xbest ∣ - 区间型指标转化为极大型指标:
M = max { a − min { x i } , max { x i } − b } , x ~ i = { 1 − a − x i M , x i < a 1 , a ≤ x i ≤ b 1 − x i − b M , , x i > b M=\max \left\{a-\min \left\{x_{i}\right\}, \max \left\{x_{i}\right\}-b\right\}, \tilde{x}_{i}= \begin{cases}1-\frac{a-x_{i}}{M}, & x_{i}b\end{cases} M=max{a−min{xi},max{xi}−b},x~i=⎩⎪⎨⎪⎧1−Ma−xi,11−Mxi−b,xi<a,a≤xi≤b,xi>b
其中[a, b]是最佳区间。
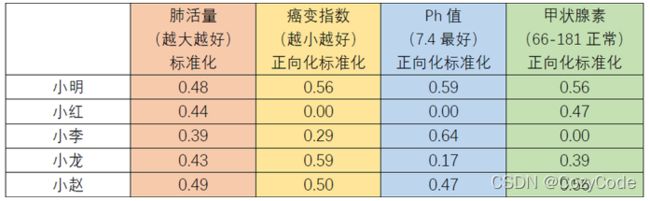
2.决策矩阵标准化
标准化的目的是消除不同指标量纲的影响,常用方法有max-min标准化和Z-score标准化,本文介绍Z-score标准化。
假设有 n n n个要评价的对象, m m m个要评价指标(已经正向化)构成的正向化矩阵如下:
X = [ x 11 x 12 ⋯ x 1 m x 21 x 22 ⋯ x 2 m ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n m ] X=\left[\begin{array}{cccc} x_{11} & x_{12} & \cdots & x_{1 m} \\ x_{21} & x_{22} & \cdots & x_{2 m} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n 1} & x_{n 2} & \cdots & x_{n m} \end{array}\right] X=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1mx2m⋮xnm⎦⎥⎥⎥⎤
,记对其进行标准化的矩阵为Z,Z中的每一个元素通过如下公式计算:
z i j = x i j / ∑ i = 1 n x i j 2 z_{i j}=x_{i j} / \sqrt{\sum_{i=1}^{n} x_{i j}^{2}} zij=xij/i=1∑nxij2
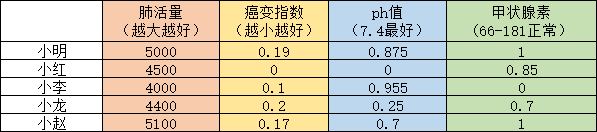
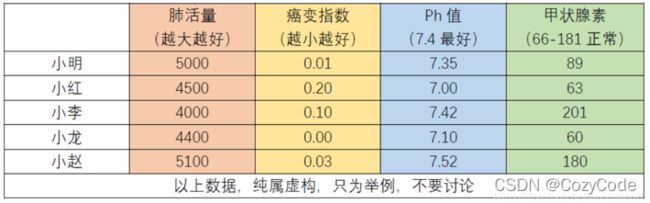
例:下表是5位同学身体相关参数,请用TOPSIS法来对同学身体情况进行一个综合的评价。
3.计算得分并归一化
假设有 n n n个要评价的对象, m m m个要评价指标构成的标准化矩阵如下:
Z = [ z 11 z 12 ⋯ z 1 m z 21 z 22 ⋯ z 2 m ⋮ ⋮ ⋱ ⋮ z n 1 z n 2 ⋯ z n m ] Z=\left[\begin{array}{cccc} z_{11} & z_{12} & \cdots & z_{1 m} \\ z_{21} & z_{22} & \cdots & z_{2 m} \\ \vdots & \vdots & \ddots & \vdots \\ z_{n 1} & z_{n 2} & \cdots & z_{n m} \end{array}\right] Z=⎣⎢⎢⎢⎡z11z21⋮zn1z12z22⋮zn2⋯⋯⋱⋯z1mz2m⋮znm⎦⎥⎥⎥⎤
定义最大值
Z + = ( Z 1 + , Z 2 + , ⋯ , Z m + ) = ( max { z 11 , z 21 , ⋯ , z n 1 } , max { z 12 , z 22 , ⋯ , z m 2 } , ⋯ , max { z 1 m , z 2 m , ⋯ , z m m } ) \begin{array}{rlr} Z^{+} & =\left(Z_{1}^{+}, Z_{2}^{+}, \cdots, Z_{m}^{+}\right) \\ & =\left(\max \left\{z_{11}, z_{21}, \cdots, z_{n 1}\right\}, \max \left\{z_{12}, z_{22}, \cdots, z_{m 2}\right\}, \cdots, \max \left\{z_{1 m}, z_{2 m}, \cdots, z_{m m}\right\}\right) \end{array} Z+=(Z1+,Z2+,⋯,Zm+)=(max{z11,z21,⋯,zn1},max{z12,z22,⋯,zm2},⋯,max{z1m,z2m,⋯,zmm})
定义最小值
Z − = ( Z 1 − , Z 2 − , ⋯ , Z m − ) = ( min { z 11 , z 21 , ⋯ , z n 1 } , min { z 12 , z 22 , ⋯ , z n 2 } , ⋯ , min { z 1 m , z 2 m , ⋯ , z n m } ) \begin{aligned} Z^{-} &=\left(Z_{1}^{-}, Z_{2}^{-}, \cdots, Z_{m}^{-}\right) \\ &=\left(\min \left\{z_{11}, z_{21}, \cdots, z_{n 1}\right\}, \min \left\{z_{12}, z_{22}, \cdots, z_{n 2}\right\}, \cdots, \min \left\{z_{1 m}, z_{2 m}, \cdots, z_{n m}\right\}\right) \end{aligned} Z−=(Z1−,Z2−,⋯,Zm−)=(min{z11,z21,⋯,zn1},min{z12,z22,⋯,zn2},⋯,min{z1m,z2m,⋯,znm})
定义第 i i i个评价对象与最大值的距离 D i + = ∑ j = 1 m ( Z j + − z i j ) 2 D_{i}^{+}=\sqrt{\sum_{j=1}^{m}\left(Z_{j}^{+}-z_{i j}\right)^{2}} Di+=∑j=1m(Zj+−zij)2
定义第 i i i个评价对象与最小值的距离 D i − = ∑ j = 1 m ( Z j − − z i j ) 2 D_{i}^{-}=\sqrt{\sum_{j=1}^{m}\left(Z_{j}^{-}-z_{i j}\right)^{2}} Di−=∑j=1m(Zj−−zij)2
那么我们就可以计算得出第 i i i个评价对象未归一化的得分: S i = D i − D i + + D i − S_{i}=\frac{D_{i}^{-}}{D_{i}^{+}+D_{i}^{-}} Si=Di++Di−Di−
很明显 0 ≤ S i ≤ 1 0 \leq S_{i} \leq 1 0≤Si≤1,且 S i S_i Si越大 D i + D_i^+ Di+越小,即越接近最大值。
最后我们可以将得分归一化: S ~ i = S i / ∑ i = 1 m S i \tilde{S}_{i}=S_{i} / \sum\limits_{i=1}^{m} S_{i} S~i=Si/i=1∑mSi,可以得知 ∑ i = 1 m S ~ i = 1 \sum\limits_{i=1}^{m} \tilde{S}_{i} = 1 i=1∑mS~i=1
建模完毕。
三、TOPSIS与(组合)赋权法结合
假设有 n n n个要评价的对象, m m m个要评价指标构成的标准化矩阵如下:
Z = [ z 11 z 12 ⋯ z 1 m z 21 z 22 ⋯ z 2 m ⋮ ⋮ ⋱ ⋮ z n 1 z n 2 ⋯ z n m ] Z=\left[\begin{array}{cccc} z_{11} & z_{12} & \cdots & z_{1 m} \\ z_{21} & z_{22} & \cdots & z_{2 m} \\ \vdots & \vdots & \ddots & \vdots \\ z_{n 1} & z_{n 2} & \cdots & z_{n m} \end{array}\right] Z=⎣⎢⎢⎢⎡z11z21⋮zn1z12z22⋮zn2⋯⋯⋱⋯z1mz2m⋮znm⎦⎥⎥⎥⎤
可以使用层次分析法或者熵权法给这 m m m个评价指标赋权
D i + = ∑ j = 1 m ω j ( Z j + − z i j ) 2 D_{i}^{+}=\sqrt{\sum_{j=1}^{m} \omega_{j}\left(Z_{j}^{+}-z_{i j}\right)^{2}} Di+=j=1∑mωj(Zj+−zij)2
D i − = ∑ j = 1 m ω j ( Z j − − z i j ) 2 D_{i}^{-}=\sqrt{\sum_{j=1}^{m} \omega_{j}\left(Z_{j}^{-}-z_{i j}\right)^{2}} Di−=j=1∑mωj(Zj−−zij)2
代码
基于熵权法对上例进行求解(matlab)。
%基于熵权法对于TOPSIS的修正
clear;clc;
load X.mat;
%获取行数列数
r = size(X,1);
c = size(X,2);
%首先,把我们的原始指标矩阵正向化
%第二列中间型--->极大型
middle = input("请输入最佳的中间值:");
M = max(abs(X(:,2)-middle));
for i=1:r
X(i,2) = 1-abs(X(i,2)-middle)/M;
end
%第三列极小型--->极大型
max_value = max(X(:,3));
X(:,3) = abs(X(:,3)-max_value);
%第四列区间型--->极大型
a = input("请输入区间的下界:");
b = input("请输入区间的下界:");
M = max(a-min(X(:,4)),max(X(:,4))-b);
for i=1:r
if (X(i,4)<a)
X(i,4) = 1-(a-X(i,4))/M;
elseif (X(i,4)<=b&&X(i,4)>=a)
X(i,4) = 1;
else
X(i,4) = 1-(X(i,4)-b)/M;
end
end
disp("正向化后的矩阵为:");
disp(X);
%然后对正向化后的矩阵进行熵权法赋权重
tempX = X; %代替X进行计算的辅助变量,避免X受到影响而发生改变
%测试:tempX = [1,2,3;-1,0,-6;5,-3,2];
%标准化矩阵,消除负数项,并且把数值控制在0-1区间
min = min(tempX);
max = max(tempX);
min = repmat(min,size(tempX,1),1);
max = repmat(max,size(tempX,1),1);
tempX = (tempX-min)./(max-min);
%求出矩阵的概率矩阵,即能取到该值的概率
sumX = repmat(sum(tempX),size(tempX,1),1);
pX = tempX./sumX;
%求出信息熵矩阵,信息熵越大,能获得的信息就越少
temp = pX.*mylog(pX);
n = size(tempX,1);
sum1 = sum(temp);
eX = sum1.*(-1/log(n));
%求出信息效用值
dX = 1-eX;
%求出每个指标的熵权
wX = dX./(sum(dX));
%打印输出
disp("每个指标依次的熵权为:");
disp(wX);