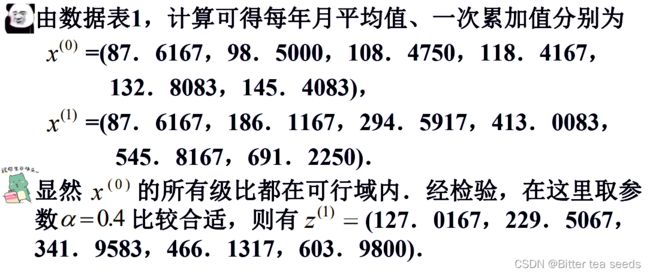
数学建模算法与应用:预测模型(3)案例: SARS 疫情对经济指标影响
目录
问题描述:
一、建模思路
二、对模型进行分析预测
2.1、对模型进行假设
三、建立灰色预测模型GM(1,1)
3.1、模型的求解(i)商品零售额
3.2、用MATLAB程序,实现(i)商品零售额
3.3、输出结果
3.4、模型的求解(ii)接待海外旅游人数
四、结果分析
问题描述:
2003年的 SARS 疫情对中国部分行业的经济发展产生了一定的影响,特别是对部分疫情较严重的省市的相关行业所造成的影响是明显的,经济影响主要分为直接经济影响和间接影响.直接经济影响涉及到商品零售业、旅游业、综合服务等行业.很多方面难以进行定量地评估,现仅就 SARS 疫情较重的某市商品零售业、旅游业和综合服务业的影响进行定量的评估分析。
那么究竟 SARS 疫情对商品零售业、旅游业和综合服务业的影响有多大,已知该市从1997年1月到2003年10月的商品零售额、接待旅游人数和综合服务收入的统计数据如下表1、表2、表3。
表一:商品的零售额(单位:亿元)
| 年代 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1997 | 83.0 | 79.8 | 78.1 | 85.1 | 86.6 | 88.2 | 90.3 | 86.7 | 93.3 | 92.5 | 90.9 | 96.9 |
| 1198 | 101.7 | 85.1 | 87.8 | 91.6 | 93.4 | 94.5 | 97.4 | 99.5 | 104.2 | 102.3 | 101.0 | 123.5 |
| 1999 | 92.2 | 114.0 | 93.3 | 101.0 | 103.5 | 105.2 | 109.5 | 109.2 | 109.6 | 111.2 | 121.7 | 131.3 |
| 2000 | 105.0 | 125.7 | 106.6 | 116.0 | 117.6 | 118.0 | 121.7 | 118.7 | 120.2 | 127.8 | 121.8 | 121.9 |
| 2001 | 139.3 | 129.5 | 122.5 | 124.5 | 135.7 | 130.8 | 138.7 | 133.7 | 136.8 | 138.9 | 129.6 | 133.7 |
| 2002 | 137.5 | 135.3 | 133.0 | 133.4 | 142.8 | 141.6 | 142.9 | 147.3 | 159.6 | 162.1 | 153.5 | 155.9 |
| 2003 | 163.2 | 159.7 | 158.4 | 145.2 | 124 | 144.1 | 157 | 162.6 | 171.8 | 180.7 | 173.5 | 176.5 |
表二:接待海外旅游人数(单位:万人)
| 年代 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1997 | 9.4 | 11.3 | 16.8 | 19.8 | 20.3 | 18.8 | 20.9 | 24.9 | 24.7 | 24.3 | 19.4 | 18.6 |
| 1198 | 9.6 | 11.7 | 15.8 | 19.9 | 19.5 | 17.8 | 17.8 | 23.3 | 21.4 | 24.5 | 20.1 | 15.9 |
| 1999 | 10.1 | 12.9 | 17.7 | 21.0 | 21.0 | 20.4 | 21.9 | 25.8 | 29.3 | 29.8 | 23.6 | 16.5 |
| 2000 | 11.4 | 26.0 | 19.6 | 25.9 | 27.6 | 24.3 | 23.0 | 27.8 | 27.3 | 28.5 | 32.8 | 18.5 |
| 2001 | 11.5 | 26.4 | 20.4 | 26.1 | 28.9 | 28.0 | 25.2 | 30.8 | 28.7 | 28.1 | 22.2 | 20.7 |
| 2002 | 13.7 | 29.7 | 23.1 | 28.9 | 29.0 | 27.4 | 26.0 | 32.2 | 31.4 | 32.6 | 29.2 | 22.9 |
| 2003 | 15.4 | 17.1 | 23.5 | 11.6 | 1.78 | 2.61 | 8.8 | 16.2 | 20.1 | 24.9 | 26.5 | 21.8 |
表三:综合服务业累计数据(单位:亿元)
| 年代 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1997 | 无 | 96 | 144 | 194 | 276 | 383 | 466 | 554 | 652 | 747 | 832 | 972 |
| 1198 | 111 | 169 | 235 | 400 | 459 | 565 | 695 | 805 | 881 | 1011 | 1139 | |
| 1999 | 151 | 238 | 335 | 425 | 541 | 641 | 739 | 866 | 975 | 1087 | 1238 | |
| 2000 | 164 | 263 | 376 | 531 | 600 | 711 | 913 | 1038 | 1173 | 1296 | 1497 | |
| 2001 | 182 | 318 | 445 | 576 | 708 | 856 | 1000 | 1145 | 1292 | 1435 | 1667 | |
| 2002 | 216 | 361 | 504 | 642 | 818 | 979 | 1142 | 1305 | 1479 | 1644 | 1920 | |
| 2003 | 241 | 404 | 584 | 741 | 923 | 1114 | 1298 | 1492 | 1684 | 1885 | 2218 |
试根据这些历史数据建立预测评估模型,评估2003年SARS疫情给该市的商品零售业、旅游业和综合服务业所造成的影响。
一、建模思路
(1)、找到商品零售业、旅游业和综合服务业的历年的的基本水平,在没有疫情的情况下进行分析,在未来的某一年应该达到怎样的水平,再与实际的水平做一个比较,就得到具体的结论。
(2)、 根据每年的某个月来预测2003年的某个月的数据,例用每年2月的数据来预测2003年2月的数据。
(3)、对每年的每个月的和进行预测,然后要预测某个月,把这个月的数据每年占总和的比例进行预测,然后用2003年的某个月的比例乘以总和就是这个月的数据。
二、对模型进行分析预测
根据所掌握的历史统计数据可以看出,在正常情况下,全年的平均值较好地反映了相关指标的变化规律(所以我们按照第一种思路进行建模分析)。
这样可以把预测评估分成两部分:
1、利用灰色理论建立灰微分方程模型,由1997~2002年的平均值预测2003年平均值;
2、通过历史数据计算每个月的指标值与全年总值的关系,从而可预测出正常情况下2003年每个月的指标值,再与实际值比较可以估算出 SARS 疫情实际造成的影响。
2.1、对模型进行假设
给出下面两条假设:
(1)假设该市的统计数据都是可靠准确的;
(2)假设该市在 SARS 疫情流行期间和结束之后,数据的变化只与 SARS 疫情的影响有关,不考虑其他随机因素的影响。
三、建立灰色预测模型GM(1,1)
灰色模型GM(1,1)的详细介绍在我的专栏《MATLAB数学建模算法与应用》的预测模型(2),有详细讲解和实例分析,这里就不在进行重复的介绍了。
3.1、模型的求解(i)商品零售额
问:![]() 为什么取0.4,不应该取0.5吗?
为什么取0.4,不应该取0.5吗?
答:因为取0.5的话,不符合构建灰色预测模型的条件,取0.4则符合灰色预测模型的范围。
问: ![]() 数据是怎么求的呢?
数据是怎么求的呢?
答:![]() 是
是![]() 的均值生成序列;
的均值生成序列; ![]()
满足以上条件,具体的介绍在我的专栏《MATLAB数学建模算法与应用》的预测模型(2)中
3.2、用MATLAB程序,实现(i)商品零售额
代码如下所示:
han1=[83.0,79.8,78.1,85.1,86.6,88.2,90.3,86.7,93.3,92.5,90.9,96.9;
101.7,85.1,87.8,91.6,93.4,94.5,97.4,99.5,104.2,102.3,101.0,123.5;
92.2,114.0,93.3,101.0,103.5,105.2,109.5,109.2,109.6,111.2,121.7,131.3;
105.0,125.7,106.6,116.0,117.6,118.0,121.7,118.7,120.2,127.8,121.8,121.9;
139.3,129.5,122.5,124.5,135.7,130.8,138.7,133.7,136.8,138.9,129.6,133.7;
137.5,135.3,133.0,133.4,142.8,141.6,142.9,147.3,159.6,162.1,153.5,155.9;
163.2,159.7,158.4,145.2,124,144.1,157,162.6,171.8,180.7,173.5,176.5]
han1(end,:)=[];%相当于han1=han1(1:6:);
m=size(han1,2);%把月份提取出来
x0=mean(han1,2);%返回x矩阵每行的平均值,其中的2代表返回行
x1=cumsum(x0)%一次累加
alpha=0.4;n=length(x0);
z1=alpha*x1(2:n)+(1-alpha)*x1(1:n-1)%求邻域生成数
Y=x0(2:n);B=[-z1,ones(n-1,1)];
ab=B\Y
k=6;
x7hat=(x0(1)-ab(2)/ab(1))*(exp(-ab(1)*k)-exp(-ab(1)*(k-1)))
z=m*x7hat
u=sum(han1)/sum(sum(han1)) %sum(han1)是每一列的数据,sum(sum(han1))是每一列加每一行总的数据,相当于每一月的均值
v=z*u
3.3、输出结果
han1 =
列 1 至 11
83.0000 79.8000 78.1000 85.1000 86.6000 88.2000 90.3000 86.7000 93.3000 92.5000 90.9000
101.7000 85.1000 87.8000 91.6000 93.4000 94.5000 97.4000 99.5000 104.2000 102.3000 101.0000
92.2000 114.0000 93.3000 101.0000 103.5000 105.2000 109.5000 109.2000 109.6000 111.2000 121.7000
105.0000 125.7000 106.6000 116.0000 117.6000 118.0000 121.7000 118.7000 120.2000 127.8000 121.8000
139.3000 129.5000 122.5000 124.5000 135.7000 130.8000 138.7000 133.7000 136.8000 138.9000 129.6000
137.5000 135.3000 133.0000 133.4000 142.8000 141.6000 142.9000 147.3000 159.6000 162.1000 153.5000
163.2000 159.7000 158.4000 145.2000 124.0000 144.1000 157.0000 162.6000 171.8000 180.7000 173.5000
列 12
96.9000
123.5000
131.3000
121.9000
133.7000
155.9000
176.5000
x1 =
87.6167
186.1167
294.5917
413.0083
545.8167
691.2250
z1 =
127.0167
229.5067
341.9583
466.1317
603.9800
ab =
-0.0993
85.5985
x7hat =
162.8793
z =
1.9546e+03
u =
列 1 至 11
0.0794 0.0807 0.0749 0.0786 0.0819 0.0818 0.0845 0.0838 0.0872 0.0886 0.0866
列 12
0.0920
v =
列 1 至 11
155.2152 157.7365 146.4023 153.5421 160.1400 159.8337 165.0649 163.7924 170.5317 173.1473 169.3064
列 12
179.83943.4、模型的求解(ii)接待海外旅游人数
预测步骤和商品零售额的预测是一摸一样的