【数独 2】候选数法解数独谜题-挖掘更深的信息-C++实现
前言
- 前面已经介绍了用候选数法来解数独谜题。
还没看的朋友点这里哦:【数独 1】不回溯,试试候选数法1ms高效解数独谜题-C++实现- 接下来在前一节算法的基础上进行一些改进,使模型可解更多的数独谜题。
- 本解的方法利用区块摒除法和数对法的思路实现,下面会先介绍这两种数独谜题的解法。
文章目录
- 前言
- 区块摒除法过程
- 数对法过程
- 程序的实现
-
- 1. 区块摒除
- 2. 数对
- 总结
区块摒除法过程
区块摒除法是人玩数独游戏时常用的一种解法。
- 如果在一个小九宫中,某个数字剩下的候选数都在同行(列),则可以摒除该行(列)其它位置该数字出现的可能性。
- 如果在一行(列)中,某个数字剩下的候选数豆子同一小九宫中,则可以摒除该小九宫其它位置该数字出现的可能性。
例子:
对下图情况,可以首先数字6对第五宫摒除,得到第五宫的6在R4C5或R6C5,不论是在R4C5还是R6C5,此时C5这一列的其他单元格都不能再有数字6。结合第一宫和第三宫的数字6对第二宫的摒除,我们可以确定,第二宫的数字6在R1C4。
数对法过程
数对法的使用条件比区块摒除法更苛刻
- 如果在一(行 / 列 / 小九宫)中,两个不同的数字剩余的候选数恰好都在同样的两个格子中,则可以排除这两个格子中的其它候选数。
例子:
如下图所示,通过数字2和7对第一宫的摒除,我们发现出现了这样的情况:在第一宫中,2和7两个数字的候选位置占用了相同的两个单元格。于是可以肯定,这两个单元格中只能是2和7,从而摒除了其他数字出现在这两个单元格中的可能。
在下图的例子中,我们再利用8对C1列的摒除,就可以确定第一宫中的数字8位于R1C3。
- 刚刚我们介绍了两种解数独的方法,但是要怎么把它们实现到我们的程序中来呢?继续往下面看吧!
程序的实现
首先我们考虑数据的表示,我们使用两个全局变量,其中一个二维数组s来存储我们的数独盘面,另一个三维数组p来存储我们的候选数。
bool p[10][10][10]{}; //(行,列,值)
int s[10][10]{}; //(行,列)
其中我们存储候选数的三维数组p在逻辑上可以理解成像下图的样子,
p[3][4][2]=1表示数独第3行第4列的数字2处于候选状态。相反,如果值为p值为0则表示相应的候选数已经被排除了。
接下来我们看具体的算法实现。
1. 区块摒除
区块摒除法在程序中将被实现成一个扫描
p数组的过程,扫描寻找的情况可以分为两种:
- 1)在扫描某个数字对应的矩阵时,发现矩阵的一行或一列,恰有2到3个为1的值,而这些1值都位于同一个小九宫中。
则在对应的数字矩阵中,就可以排除小九宫中其它的1值。- 2)在扫描某个数字对应的矩阵时,发现矩阵的一个小九宫中恰有2到3个为1的值,而这些1值都位于同一行或同一列中。
同样的,我们在对应的数字矩阵中,就可以排除同行或同列中其它的1值。
源代码:
void change_p_remain() {
/*扫描每个数值矩阵*/
for(int k = 1; k <= 9; ++k) {
/*宫中余同行列*/
for(int i = 1; i <= 9; i += 3) {
for(int j = 1; j <= 9; j += 3) {
int count_1(0); /*1的数量*/
int m[9]{}, n[9]{}; /*(m,n)*/
/*扫描一个宫*/
for(int u = i; u <= i + 2; ++u) {
for(int v = j; v <= j + 2; ++v) {
if(p[u][v][k] == 1) {
m[count_1] = u;
n[count_1] = v;
count_1++;}}}
if(count_1 == 2) { /*为了合并count_1为2,3的两种情况,简化代码*/
m[2] = m[0];
n[2] = n[0];}
if(count_1 == 2 || count_1 == 3) {
if(m[0] == m[1] && m[0] == m[2]) {
/*摒除第m行*/
for(int x = 1; x <= 9; ++x) {
if(x != n[0] && x != n[1] && x != n[2]) {
p[m[0]][x][k] = 0;}}}
else if(n[0] == n[1] && n[0] == n[2]) {
/*摒除第n列*/
for(int x = 1; x <= 9; ++x) {
if(x != m[0] && x != m[1] && x != m[2]) {
p[x][n[0]][k] = 0;}}}}}}
//*行列中余同宫*/
for(int i = 1; i <= 9; ++i) {
int count_1(0);
int n[9]{};
// *扫描一行*
for(int j = 1; j <= 9; ++j) {
if(p[i][j][k] == 1) { //*(i,n)为p真的位置*
n[count_1] = j;
count_1++;}}
if(count_1 == 2) {
n[2] = n[0];}
if(count_1 == 2 || count_1 == 3) {
if(where_small(n[0]) == where_small(n[1]) && where_small(n[0]) == where_small(n[2])) {
//*摒除(i,n)之宫*
int u = where_small(i);
int v = where_small(n[0]);
for(int x = u; x <= u + 2; ++x) {
for(int y = v; y <= v + 2; ++y) {
if(x != i || (y != n[0] && y != n[1] && y != n[2])) {
p[x][y][k] = 0;}}}}} //*p置零*
//*扫描一列*
for(int j = 1; j <= 9; ++j) {
if(p[j][i][k] == 1) { //*(n,i)为p真的位置* /*(j,i)与行扫描反*
n[count_1] = j;
count_1++;}}
if(count_1 == 2) {
n[2] = n[0];} //*变的是n了*
if(count_1 == 2 || count_1 == 3) {
if(where_small(n[0]) == where_small(n[1]) && where_small(n[0]) == where_small(n[2])) {
//*摒除同宫*
int u = where_small(n[0]);
int v = where_small(i);
for(int x = u; x <= u + 2; ++x) {
for(int y = v; y <= v + 2; ++y) {
if(y != i || (x != n[0] && x != n[1] && x != n[2])) {
p[x][y][k] = 0;}}}}}}}} //*p置零*
2. 数对
数对法的实现也是一个扫描
p的过程。
- 可以在一行、一列、或一小九宫中寻找数对
- 在一小九宫中寻找数对的步骤:
1)对于每个数字对于的矩阵,首先,我们逐个小九宫地扫描,如果发现一个小九宫中只有两个1值,则说明我们发现了一个存在数对的潜在可能性,于是进行下一步。
2)接下来用我们发现的这个小九宫,来和其它数字对应的矩阵来的相同宫位进行匹配。如果找到了一个完全匹配的(1值的数量和位置都相同)小九宫,则我们就找到了一个数对。
3)找到数对之后,我们就可以排除1到9所有数字对应矩阵的数对所在位置的1值。
源代码:
void do_hang(int i, int k, int n[], int h_l);
void do_gong(int k, int i, int j, int m[], int n[]);
// --------------------------------------------------
/*先实现两个数的情况*/
void change_p_pair() {
for(int k = 1; k <= 9; ++k) {
//每行发现数对
for(int i = 1; i <= 9; ++i) {
int count_m(0), count_n(0);
int m[9]{}, n[9]{}; //行扫描n作列标,列扫描m作行标
for(int j = 1; j <= 9; ++j) {
if(p[i][j][k] == 1) { //行扫
n[count_n] = j;
count_n++;}
if(p[j][i][k] == 1) { //列扫
m[count_m] = j;
count_m++;}}
if(count_n == 2) {
do_hang(i, k, n, 0);}
if(count_m == 2) {
do_hang(i, k, m, 1);}}
//每宫发现数对
for(int i = 1; i <= 9; i += 3) {
for(int j = 1; j <= 9; j += 3) {
int count(0);
int m[9]{}, n[9]{};
for(int x = i; x <= i + 2; ++x) {
for(int y = j; y <= j + 2; ++y) {
if(p[x][y][k] == 1) {
m[count] = x;
n[count] = y;
count++;}}}
if(count == 2) {
do_gong(k, i, j, m, n);}}}}}
// --------------------------------------------------
/*
*功能:宫匹配与处理
*参数:k为数值矩阵号,(i,j)为目标宫的始下标*/
void do_gong(int k, int i, int j, int m[], int n[]) {
for(int l = 1; l <= 9; ++l) { //l迭代匹配矩阵
if(l == k) continue;
int flag(1);
for(int x = i; x <= i + 2; ++x) {
for(int y = j; y <= j + 2; ++y) {
if(p[x][y][k] != p[x][y][l]) {
flag = 0;
break;}}}
if(flag) {
for(int h = 1; h <= 9; ++h) { //h迭代更新矩阵
if(h == l || h == k) continue;
p[m[0]][n[0]][h] = 0;
p[m[1]][n[1]][h] = 0;}}}}
// --------------------------------------------------
/*
*功能:行列匹配与处理
*参数:h_l标志原来是行扫描(0)还是列扫描(1)*/
void do_hang(int i, int k, int n[], int h_l) {
if(h_l == 0)
for(int l = 1; l <= 9; ++l) { //l为其它数值矩阵,与k矩阵尝试匹配
if(l == k) continue; //不和自己比
int flag(1);
for(int j = 1; j <= 9; ++j) { //比较
if(p[i][j][l] != p[i][j][k]) {
flag = 0;
break;}}
if(flag == 1) { //成功找到数对,更新p
for(int h = 1; h <= 9; ++h) { //h迭代数值矩阵
//(注意)每一次迭代结束,i,n[0],n[1]不变
if(h == k || h == l) continue;
p[i][n[0]][h] = 0;
p[i][n[1]][h] = 0;}}}
if(h_l == 1)
for(int l = 1; l <= 9; ++l) { //l为其它数值矩阵,与k矩阵尝试匹配
if(l == k) continue; //不和自己比
int flag(1);
for(int j = 1; j <= 9; ++j) { //比较
if(p[j][i][l] != p[j][i][k]) {
flag = 0;
break;}}
if(flag == 1) { //成功找到数对,更新p
for(int h = 1; h <= 9; ++h) { //h迭代数值矩阵
if(h == k || h == l) continue;
p[n[0]][i][h] = 0;
p[n[1]][i][h] = 0;}}}}
在实现了上面两个方法后,只需要在原来的主函数中
change_p();的位置加上这两个函数的调用就可以啦!
主函数源代码:
/*主函数*/
int main() {
while(true) { //每次循环输入一个新的谜题进行求解
init_s();
init_p();
in_s();
clock_t start(0), finish(0);
start = clock();
int i = 0;
for(i = 0; i < 81; ++i) { //解数独
change_p();
//----------新的函数
change_p_remain();
change_p_pair();
//----------
change_s();
if(enough_s()) break; //已经得到解时,停止循环
}
finish = clock();
cout << "循环次数为:" << (i + 1) << endl;
cout << "The time is " << (finish - start) << " ms " << endl;
out_s();
system("pause");
system("cls");
}
return 0;
}
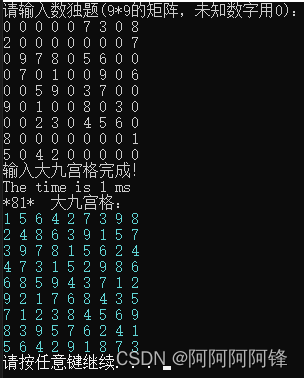
测试数据:
0 0 0 0 0 7 3 0 8
2 0 0 0 0 0 0 0 7
0 9 7 8 0 5 6 0 0
0 7 0 1 0 0 9 0 6
0 0 5 9 0 3 7 0 0
9 0 1 0 0 8 0 3 0
0 0 2 3 0 4 5 6 0
8 0 0 0 0 0 0 0 1
5 0 4 2 0 0 0 0 0
这是上一节不能解决的一个数独谜题,现在已经可以填出全部的数字啦!
总结
相比上次,现在的程序已经强大很多啦!可以解出更多的数独谜题(依旧不是全部,仍然有待努力),满满的成就感。
数独题库:尤怪之家数独挑战馆出题菜单
有兴趣的朋友们可以尝试用这个网站中的数独来测试程序。
都已经白嫖到这里了,不给博主来个点赞关注加收藏再走?
你们的支持就是博主不断写作的动力!