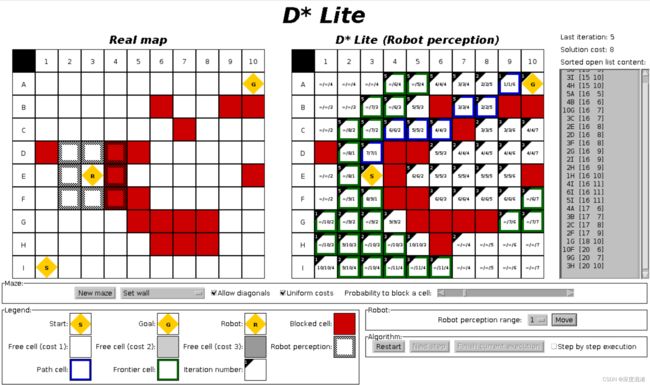
C#，人工智能，机器人路径规划（Robotics Pathfinding）DStarLite（D* Lite Algorithm）优化算法与C#源程序

 文章与图片都是抄的，程序可是一脚一脚撸的。

一、DStarLite算法摘要

Dstar Lite是一种复杂的寻路算法，在机器人和游戏设计等许多领域都有实际应用。该算法能够解决最短路径问题，还集成了其他功能，如路径重新规划和路径校正。通过使用计算机模拟和分析该算法，我们测试了该算法的能力和处理速度，看看它是否可以成为高中机器人竞赛环境中的可行工具。最终，我们发现Dstar Lite的工作效率高于类似算法，因为它提供了一条从开始到结束的快速可靠的路径。我们建议机器人团队在自己的机器人代码中实现该算法，并将其用于自主运动。

二、DStarLite算法介绍

Dstar Lite是一种寻路算法，允许程序员在已知或部分已知的环境中找到起点和终点之间的最佳路径。该算法设计为在由边连接的节点组成的图数据结构上运行。指向探路器所在的当前位置的节点称为前置节点，而当前节点指向的节点称为其后续节点。

Dstar Lite的工作原理是跟踪给定图形上每个节点的两个分数。第一个分数是G分数。该值跟踪到达图形上某个位置的成本。可以将其视为连接起点和当前点的最短路径。对于起点，G分数为零，因为探路者已经在那里了。另一方面，RHS分数是一个更有用的估计值。该分数作为一步向前看，在算法中，它用于找到探路者要前往的下一个最佳位置。如果下一个位置是障碍物，则连接成本将设置为无穷大，因为探路者永远无法到达该点。因此，RHS分数也是无穷大的。利用这两个分数，该算法将路径从终点传播到起点，最终找到从起点到终点的最优路径。

Terminology:
S = current node
S’ = predecessor node
C (s’, s) = edge cost for s’ ? s
G(s) = current cost to arrive at that node
G(s) = G(s’) + C (S’, S)
RHS(s) = min value((G(S’) + C (S’, S))

G分数和RHS分数作为Dstar Lite路径规划和重新规划的基础。如果Dstar Lite算法遇到不可预见的障碍并被迫重新规划路径，则只需使用所有受影响节点的新连接成本重新计算RHS分数。Koenig和Likhachev关于Dstar Lite算法的论文中有更详细的解释。

该算法在工业上有许多实际应用。最著名的是，当蜂窝信号必须通过中继来自蜂窝塔网络的信号来找到从起点到目的地的最佳路径时，Dstar Lite用于电信行业。此外，该算法通常最适合机器人领域的路径规划。Dstar Lite允许在动态环境中快速重新种植。该功能对机器人很有用，因为在现实世界中，环境不断变化，机器人需要能够避开障碍物并快速重新规划其路径。

在2002年开发Dstar Lite之前，其他算法（如Astar和Dijkstra算法）主导了路径搜索领域。Dstar Lite与这些路径优化算法主要有两个不同之处。首先，Dijkstra和Astar要求用户完全了解环境，因为它们不提供内置的重新规划功能。这种差异意味着，如果机器人遇到未知的东西，Astar和Dijkstra的算法将需要完全重新运行，以便创建新的路径。另一方面，Dstar Lite只快速重新计算受影响的区域，从而显著减少了必要的处理时间。当检测到节点是障碍物时，到达该节点的成本变为无穷大，因此RHS分数更新为无穷大。其次，Astar和Dijkstra的算法从生成一条从头到尾的路径开始。另一方面，Dstar Lite生成从目标到起点的路径。这种差异对于重新规划很有用，因为当需要重新生成路径时，向后遍历时需要的更改更少。

在本文中，我们将讨论Dstar Lite如何成为机器人领域以及高中机器人比赛中使用的有效算法。我们相信，该算法的功能可以用于自主运动和辅助导航。

三、DStarLite算法的计算结果和讨论

我们使用模拟进行的第一个测试研究了运行时间如何随着网格大小的增加而变化。在我们的测试中，我们使用了网格长度和宽度，从10×10开始，然后慢慢增加大小，直到达到500×500。通过该测试，我们观察到，随着网格尺寸的增加，运行时间急剧增长。这是因为当网格的长度和宽度增加时，瓷砖的数量（等于长度乘以宽度）呈二次增长。当Dstar Lite穿过网格时，它必须检查与其直接相邻的8个磁贴。当总网格中有更多坐标时，Dstar Lite会整体检查更多的图块，因此运行时间会急剧增加。

接下来，我们测试了场地上障碍物的数量如何影响运行时间。这个结果更令人惊讶，因为我们看到，随着网格上放置更多障碍，运行时间实际上减少了。我们认为，出现这种情况是因为网格上有更多障碍物减少了路径查找算法必须检查的点的数量。在我们的测试中，我们从10%的场地填充开始，慢慢地将充满障碍物的网格百分比增加到70%。我们注意到，随着障碍物的增加，运行时间不断减少。这一发现令人惊讶，因为我们认为更多的障碍意味着路径必须更加弯曲和不规则。相反，当存在大量障碍物时，Dstar Lite检查的点数会显著减少。

最后，我们比较了Dstar-Lite和Astar的运行时间。当算法从头到尾遍历时随机引入障碍物时，我们发现Dstar Lite比Astar算法更快。由于Astar不支持重新规划，算法必须从当前点重新运行到终点，这意味着它必须做冗余工作。另一方面，Dstar Lite在这个过程中更有效，并使用过去的信息更快地重新规划。

除了关于障碍物和场地大小的实验外，我们还测试了该算法是否能够进行路径校正。当机器人沿着一条路径行走，但由于摩擦和其他机械和物理错误，它偏离了规划的路径并最终到达其他地方时，需要进行路径校正。我们测试了Dstar-Lite算法是否可以用于重新规划路径并引导机器人返回正确的方向。我们通过在模拟机器人穿过网格时添加随机运动误差来测试这一点。每次机器人在路径中从一个瓷砖移动到下一个瓷砖时，机器人偏离正确位置并最终到达另一个相邻瓷砖的概率很小。发生这种情况时，我们使用Dstar Lite重新规划了路径，并继续沿着新生成的路径。在我们的实验中，我们看到这种行为与Dstar Lite在其路径被障碍物阻挡时的行为相同。有趣的是，当这种情况发生时，我们看到该算法要么生成一条到终点的全新路径，要么尝试修复自身并将机器人引导回原始路径。

四、有关DStarLite算法的更多讨论

Dstar Lite是一种广泛应用于机器人领域的算法。该路径规划算法可以通过里程计实现，并为真实机器人创建精确的运动轮廓功能。此外，该算法可以与传感器阵列结合使用，在机器人移动时动态避开障碍物。我们认为，该算法可以在竞争机器人中产生影响，因为该软件解决了许多问题，例如避障和精确的运动控制。目前，机器人团队在创建自主代码时面临的许多挑战可以通过将Dstar Lite算法应用到他们的软件中来解决。

在我们的实验中，我们观察到在具有少量障碍物的开放网格上，Dstar Lite的效率低于在具有许多障碍物的拥挤网格上。我们认为这是因为在我们对Dstar Lite的改编中，当一个磁贴被障碍物占据时，Dstar Lite会俯瞰该点并继续前进。这意味着，如果网格有许多障碍，探路者将跳过更多的分片，算法的处理时间将减少。这种效果似乎是有益的，因为它可以用来降低必要的处理能力，并允许更快的路径生成。

我们还发现，在每个测试期间，运行时通常有很多变化。这很可能是由测试计算机上运行的后台进程以及障碍物放置位置的可变性引起的。为了尽量减少这些影响，我们对每种情况进行了多次试验，然后平均运行时间以创建更准确的值。此外，每当在网格上放置随机障碍物时，它们产生障碍的可能性很小，因此在开始和结束之间没有可能的路径。如果出现这种情况，我们会重新设置所有障碍，然后重新进行试验。

最后，由于我们使用具有离散瓦片的网格来跟踪机器人位置，因此Dstar Lite无法生成绝对最优路径。两点之间的绝对最优路径通常是一条从起点到终点完美环绕障碍物的直线。这样的网格有八个可能要遍历的相邻点，这将限制算法生成如下图所示的真正完美路径。

可以使用视线算法解决此错误。视线算法不会仅将相邻图块视为后续图块，而是将具有直接视线的任何图块视为当前图块的后续图块。这将使生成的路径更直，调整更精细。同样，也可以通过提高图的分辨率来改善这个问题。在这种情况下，我们只需通过更多的行和列来扩大网格。这将提高路径的准确性，但运行时间也会增加。这两种方法都可以改善路径，但也意味着需要更多的处理能力和运行时间。

五、结论

在本文中，我们展示了Dstar Lite作为规划算法的有效性。我们比较了Dstar-Lite和Astar，发现前者的算法在重新规划时要快得多。我们认为，该算法在机器人领域非常有用，可以轻松地在高中机器人竞赛环境中实现。当前的高中比赛通常使用矩形网格的游戏场，在顶部放置已知和未知障碍物。Dstar Lite将能够避免这些障碍，并允许机器人快速找到最短路径。该算法不仅在创建路径方面非常有效，而且在路径重新规划和障碍回避方面比类似的算法（如Astar）更快。我们建议机器人在其自主代码中实现该算法。

六、计算方法的实现

虽然Dstar Lite最初设计为在具有特定节点的图上运行，但在我们的实验中，我们决定使用包含N行和N列的正方形网格。我们使用这种设置是因为网格可以很容易地对应于笛卡尔坐标系，并且可以在代码中表示为二维数组。这意味着（0,0）位置或网格上的原点对应于笛卡尔平面上的（0,0）位置（注意，在计算机渲染中，（0,0）点定义为左上角，下图显示了那里的原点）。此外，网格结构便于计算。在传统图中，需要隐式定义和存储每个节点之间的连接成本。对于具有许多节点和连接的图，这将快速累积并消耗内存。在我们的网格中，每个连接的成本可以自动定义为每个点之间的距离。这允许我们使用距离公式计算连接成本。类似地，需要隐式定义图的前导和后继。网格再一次优化了这个过程。网格上当前节点的前导节点和后继节点只是与其相邻的八个节点。

在网格内，机器人在坐标（0,0）（字段左上角）处初始化，最终目标设置为（N-1，N-1）（网格右下角）。这个坐标被定义为（N-1，N-1），因为我们使用2D数组作为数据结构，数组从零开始。选择这两个点是为了确保路径尽可能长，因此在创建路径的过程中，探路者需要面对更多的障碍。

最后，每次跑步前在场地上随机放置不同数量的障碍物。放置这些障碍物是为了模拟阻碍进入目标的障碍物和障碍物。此外，当机器人从起点移动到终点时，障碍物有10%的机会随机出现在机器人前面，阻塞其路径，并迫使算法重新调整路径。

通过使用我们的模拟环境，我们进行了实验，以确定该算法是否足够有效，可以用于竞争机器人环境。在许多高中机器人比赛中，要求参赛者建造自主驱动的机器人，以在复杂环境中导航，完成某项任务。我们测试了该算法在这种情况下的使用情况。

在整个实验过程中，我们研究了三个不同的因素：场大小的变化如何影响算法的运行时间，障碍物的数量如何影响运行时间，以及Dstar Lite算法与Astar算法相比如何再生最佳路径。我们使用Dstar Lite总共进行了84次试验，然后使用Astar进行了42次试验。对于每种不同的情况，我们进行了六次试验，然后取平均值。

七、References

(1) Choset, H. https://www.cs.cmu.edu/~motionplanning/lecture/AppH-astar-dstar_howie.pdf (accessed Jul 18, 2020).

(2) Koenig, S.; Likhachev, M. D* Lite. http://idm-lab.org/bib/abstracts/papers/aaai02b.pdf (accessed Jul 18, 2020).

(3) Buniyamin, N.; Sariff, N. An Overview of Autonomous Mobile Robot Path Planning Algorithms – IEEE Conference Publication. https://ieeexplore.ieee.org/abstract/document/4339335/authors#authors (accessed Jul 18, 2020).

(4) Introduction to A*. http://theory.stanford.edu/~amitp/GameProgramming/AStarComparison.html (accessed Jul 19, 2020).

(5) Konakalla, S. A Star Algorithm. http://cs.indstate.edu/~skonakalla/paper.pdf (accessed Jul 19, 2020).

(6) Language Reference (API) \ Processing 3+. https://processing.org/reference/ (accessed Jul 19, 2020).

(7) Kang, H.; Lee, B.; Kim, K. Path Planning Algorithm Using the Particle Swarm Optimization and the Improved Dijkstra Algorithm – IEEE Conference Publication. https://ieeexplore.ieee.org/abstract/document/4756927 (accessed Jul 19, 2020).

八、DStarLite算法的C#源程序

1、Point.cs

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer
{
    public class Point
    {
        public int x { get; set; } = 0;
        public int y { get; set; } = 0;

        public Point()
		{
		}

        public Point(int x, int y)
        {
            this.x = x;
            this.y = y;
        }
    }
}

2、K.cs

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer
{
    public class K
    {
        public double k1 { get; set; } = Double.PositiveInfinity;
        public double k2 { get; set; } = Double.PositiveInfinity;

		public K()
        {
        }

        public K(double K1, double K2)
        {
            k1 = K1;
            k2 = K2;
        }

        public int CompareTo(K that)
        {
            if (this.k1 < that.k1) return -1;
            else if (this.k1 > that.k1) return 1;
            if (this.k2 > that.k2) return 1;
            else if (this.k2 < that.k2) return -1;
            return 0;
        }

		public static bool operator <(K a, K b)
		{
			if (a.k1 < b.k1) return true;
			if (a.k2 < b.k2) return true;
			return false;
		}

		public static bool operator >(K a, K b)
		{
			if (a.k1 > b.k1) return true;
			if (a.k2 > b.k2) return true;
			return false;
		}

		public static bool operator ==(K a, K b)
		{
			return (Math.Abs(a.k1 - b.k1)<=float.Epsilon && 
				Math.Abs(a.k1 - b.k1)<=float.Epsilon);
		}

		public static bool operator !=(K a, K b)
		{
			return (Math.Abs(a.k1 - b.k1)>float.Epsilon || 
				Math.Abs(a.k1 - b.k1)>float.Epsilon);
		}

		public override bool Equals(object obj)
		{
			K a = (K)obj;
			return (this == a);
		}

		public override int GetHashCode()
		{
			return base.GetHashCode();
		}
    }
}

3、Heap.cs

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer
{
    public class Heap
    {
        private int n { get; set; }
        private Element[] heap;
        private Dictionary hash { get; set; }

        public Heap(int cap)
        {
            n = 0;
            heap = new Element[cap];
            hash = new Dictionary();
        }

        public K Peek()
        {
            if (n == 0)
            {
                return new K();
            }
            return heap[1].k;
        }

        public Grid Pop()
        {
            if (n == 0)
            {
                return null;
            }
            Grid s = heap[1].s;
            heap[1] = heap[n];
            hash[heap[1].s] = 1;
            hash[s] = 0;
            n--;
            Next(1);
            return s;
        }

        public void Insert(Grid s, K k)
        {
            Element e = new Element(s, k);
            n++;
            hash[s] = n;
            if (n == heap.Length)
            {
                Resize();
            }
            heap[n] = e;
            Last(n);
        }

        public void Update(Grid s, K k)
        {
            int i = hash[s];
            if (i == 0)
            {
                return;
            }
            K kold = heap[i].k;
            heap[i].k = k;
            if (kold.CompareTo(k) < 0)
            {
                Next(i);
            }
            else
            {
                Last(i);
            }
        }

        public void Remove(Grid s)
        {
            int i = hash[s];
            if (i == 0)
            {
                return;
            }
            hash[s] = 0;
            heap[i] = heap[n];
            hash[heap[i].s] = i;
            n--;
            Next(i);
        }

        public bool Contains(Grid s)
        {
            int i;
            if (!hash.TryGetValue(s, out i))
            {
                return false;
            }
            return (i != 0);
        }

        private void Next(int i)
        {
            int childL = i * 2;
            if (childL > n)
            {
                return;
            }
            int childR = i * 2 + 1;
            int smallerChild;
            if (childR > n)
            {
                smallerChild = childL;
            }
            else if (heap[childL].k.CompareTo(heap[childR].k) < 0)
            {
                smallerChild = childL;
            }
            else
            {
                smallerChild = childR;
            }
            if (heap[i].k.CompareTo(heap[smallerChild].k) > 0)
            {
                Swap(i, smallerChild);
                Next(smallerChild);
            }
        }

        private void Last(int i)
        {
            if (i == 1)
            {
                return;
            }
            int parent = i / 2;
            if (heap[parent].k.CompareTo(heap[i].k) > 0)
            {
                Swap(parent, i);
                Last(parent);
            }
        }

        private void Swap(int i, int j)
        {
            Element temp = heap[i];
            heap[i] = heap[j];
            hash[heap[j].s] = i;
            heap[j] = temp;
            hash[temp.s] = j;
        }

        private void Resize()
        {
            Array.Resize(ref heap, heap.Length * 2);
        }
    }
}

4、Grid.cs

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer
{
    public class Grid
    {
        public int x { get; set; } = 0;
        public int y { get; set; } = 0;
        public double g { get; set; } = Double.PositiveInfinity;
        public double rhs { get; set; } = Double.PositiveInfinity;
        public bool obstacle { get; set; } = false;

        public Grid(int x, int y)
        {
            this.x = x;
            this.y = y;
        }

        public override bool Equals(object that)
        {
            Grid a = that as Grid;
            return (this.x == a.x && this.y == a.y);
        }

        public static bool operator ==(Grid a, Grid b)
        {
            return a.Equals(b);
        }

        public static bool operator !=(Grid a, Grid b)
        {
            return !a.Equals(b);
        }

        public LinkedList Succesors(Grid[,] map)
        {
            LinkedList s = new LinkedList();
            if ((x + 1) < map.GetLength(0))
            {
                s.AddFirst(map[x + 1, y]);
            }
            if ((y + 1) < map.GetLength(1))
            {
                s.AddFirst(map[x, y + 1]);
            }
            if ((x - 1) >= 0)
            {
                s.AddFirst(map[x - 1, y]);
            }
            if ((y - 1) >= 0)
            {
                s.AddFirst(map[x, y - 1]);
            }
            return s;
        }

        public LinkedList Predecessors(Grid[,] map)
        {
            LinkedList s = new LinkedList();
            Grid tempState;
            if ((x + 1) < map.GetLength(0))
            {
                tempState = map[x + 1, y];
                if (tempState.obstacle == false)
                {
                    s.AddFirst(tempState);
                }
            }
            if ((y + 1) < map.GetLength(1))
            {
                tempState = map[x, y + 1];
                if (tempState.obstacle == false)
                {
                    s.AddFirst(tempState);
                }
            }
            if ((x - 1) >= 0)
            {
                tempState = map[x - 1, y];
                if (tempState.obstacle == false)
                {
                    s.AddFirst(tempState);
                }
            }
            if ((y - 1) >= 0)
            {
                tempState = map[x, y - 1];
                if (tempState.obstacle == false)
                {
                    s.AddFirst(tempState);
                }
            }
            return s;
        }

        public override int GetHashCode()
        {
            return base.GetHashCode();
        }
    }
}

5、Environment.cs

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer
{
    public interface DStarLiteEnvironment
    {
        void MoveTo(Point s);

        LinkedList GetObstaclesInVision();
    }
}

6、Element.cs

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer
{
    public class Element
    {
        public Grid s { get; set; }    
        public K k { get; set; }

        public Element(Grid g, K k)
        {
            this.s = g;
            this.k = k;
        }
    }
}

7、DStarLite.cs

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer
{
    public class DStarLite
    {
        private int Row { get; set; }
        private int Column { get; set; }
        private Heap Path { get; set; }
        private Grid[,] Map { get; set; }
        private Grid Start { get; set; }
        private Grid Goal { get; set; }
        private double Factor { get; set; }

        public void Execute(int n, int m, int sx, int sy, int gx, int gy, DStarLiteEnvironment env)
        {
            Row = n;
            Column = m;
            Start = new Grid(sx, sy);
            Goal = new Grid(gx, gy);
            Grid slast = Start;
            Initialize();
            FindShortestPath();          
            while (Start != Goal)
            {
                Start = FindMiniumGrid(Start);
                env.MoveTo(new Point(Start.x, Start.y));
                LinkedList obstacleCoord = env.GetObstaclesInVision();
                double old_factor = Factor;
                Grid oldslast = slast;
                Factor += Heuristic(Start, slast);
                slast = Start;
                bool change = false;
                foreach (Point c in obstacleCoord)
                {
                    Grid s = Map[c.x, c.y];
                    if (s.obstacle)
                    {
                        continue;
                    }
                    change = true;
                    s.obstacle = true;
                    foreach (Grid p in s.Predecessors(Map))
                    {
                        UpdatePath(p);
                    }
                }
                if (change == false)
                {
                    Factor = old_factor;
                    slast = oldslast;
                }
                FindShortestPath();
            }
        }

        private K CalculateKey(Grid s)
        {
            return new K(Math.Min(s.g, s.rhs) + Heuristic(s, Start) + Factor,
                Math.Min(s.g, s.rhs));
        }

        private double Heuristic(Grid a, Grid b)
        {
            return Math.Abs(a.x - b.x) + Math.Abs(a.y - b.y);
        }

        private void Initialize()
        {
            Path = new Heap(Row * Column);
            Map = new Grid[Row, Column];
            Factor = 0.0;
            for (int i = 0; i < Row; i++)
            {
                for (int j = 0; j < Column; j++)
                {
                    Map[i, j] = new Grid(i, j);
                    Map[i, j].g = Double.PositiveInfinity;
                    Map[i, j].rhs = Double.PositiveInfinity;
                }
            }
            Start = Map[Start.x, Start.y];
            Goal = Map[Goal.x, Goal.y];
            Goal.rhs = 0;
            Path.Insert(Goal, CalculateKey(Goal));
        }

        private void UpdatePath(Grid u)
        {
            if (u != Goal)
            {
                u.rhs = MiniumCost(u);
            }
            if (Path.Contains(u))
            {
                Path.Remove(u);
            }
            if (Math.Abs(u.g - u.rhs) > float.Epsilon)
            {
                Path.Insert(u, CalculateKey(u));
            }
        }

        private Grid FindMiniumGrid(Grid u)
        {
            double min = Double.PositiveInfinity;
            Grid n = null;
            foreach (Grid s in u.Succesors(Map))
            {
                double val = 1 + s.g;
                if (val <= min && s.obstacle == false)
                {
                    min = val;
                    n = s;
                }
            }
            return n;
        }

        private double MiniumCost(Grid u)
        {
            double min = Double.PositiveInfinity;
            foreach (Grid s in u.Succesors(Map))
            {
                double val = 1.0 + s.g;
                if (val < min && s.obstacle == false)
                {
                    min = val;
                }
            }
            return min;
        }

        private void FindShortestPath()
        {
            while (Path.Peek().CompareTo(CalculateKey(Start)) < 0 ||
                Math.Abs(Start.rhs - Start.g) >= float.Epsilon) 
            {
                K kold = Path.Peek();
                Grid u = Path.Pop();
                if (u == null)
                {
                    break;
                }
                if (kold.CompareTo(CalculateKey(u)) < 0)
                {
                    Path.Insert(u, CalculateKey(u));
                }
                else if (u.g > u.rhs)
                {
                    u.g = u.rhs;
                    foreach (Grid s in u.Predecessors(Map))
                    {
                        UpdatePath(s);
                    }
                }
                else
                {
                    u.g = Double.PositiveInfinity;
                    UpdatePath(u);
                    foreach (Grid s in u.Predecessors(Map))
                    {
                        UpdatePath(s);
                    }
                }
            }
        }
    }
}

访问 深度混淆 的博客注意事项：请随意白嫖代码，但不得改为其他语言。