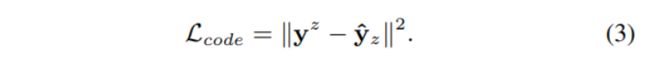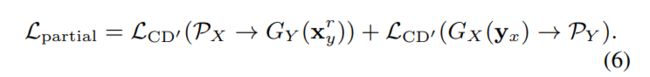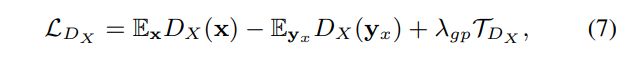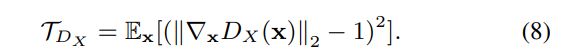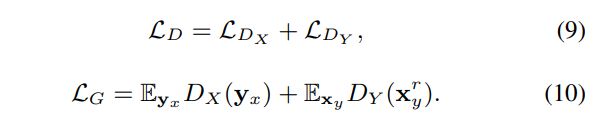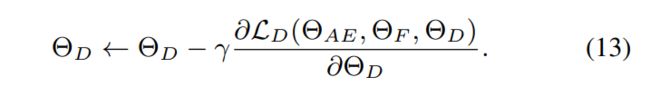【CVPR2021】Cycle4Completion:使用带缺失区域编码的循环变换实现无配对点云补全
文章目录
- Cycle4Completion: Unpaired Point Cloud Completion using Cycle Transformation with Missing Region Coding
-
- 做了什么
- Cycle4Completion
-
- 整体架构
- 缺失区域编码
- 用于学习潜在空间的编码器-解码器
- 循环变换
- 训练策略
- 实验
- 附:Chamfer距离
Cycle4Completion: Unpaired Point Cloud Completion using Cycle Transformation with Missing Region Coding
做了什么
-
提出了一种新的无配对点云完成网络——Cycle4Completion(借鉴了CycleGAN的思想,不过,输入判别器的是潜在表示)。现有的无配对点云补全方法都只考虑从缺失点云到完整点云的正向对应关系。Cycle4Completion则同时考虑正向和逆向的对应关系。
-
提出了潜在空间中的循环变换(cycle transformation)框架,该框架与部分匹配损失(partial matching loss)和循环匹配损失(cycle matching loss)相结合,建立完整和缺失形状之间的双向几何对应关系,并在整个变换过程中保持形状的一致性。
-
提出了缺失区域编码(missing region coding),将缺失形状表示分解为相应完整形状的表示和缺失区域的编码表示。这解决了网络试图基于单个完整形状预测多个缺失形状时的目标混淆问题(target confusion)。
Cycle4Completion
整体架构

P X = { p i x } \mathcal{P}_X=\{\boldsymbol{p}_i^x\} PX={pix}:缺失点云。
P Y = { p i y } \mathcal{P}_Y=\{\boldsymbol{p}_i^y\} PY={piy}:完整点云
编码器:
-
E X : P X → x E_X:\mathcal{P}_X\rightarrow\boldsymbol{x} EX:PX→x
-
E Y : P Y → y E_Y:\mathcal{P}_Y\rightarrow\boldsymbol{y} EY:PY→y
解码器:
-
G X G_X GX: x → G X ( x ) x\rightarrow G_X(x) x→GX(x)
-
G Y G_Y GY: y → G Y ( y ) y\rightarrow G_Y(y) y→GY(y)
F X F_X FX和 F Y F_Y FY(生成器)实现缺失点云 P X \mathcal{P}_X PX的潜在表示 { x } \{\boldsymbol{x}\} {x}和完整点云 P Y \mathcal{P}_Y PY的潜在表示 { y } \{\boldsymbol{y}\} {y}之间的映射:
-
F X F_X FX: x → x y \boldsymbol{x}\rightarrow \boldsymbol{x}_y x→xy,( x → y \boldsymbol{x}\rightarrow \boldsymbol{y} x→y)
-
F Y F_Y FY: y → y x \boldsymbol{y}\rightarrow \boldsymbol{y}_x y→yx,( y → x \boldsymbol{y}\rightarrow \boldsymbol{x} y→x)
-
两个函数的复合运算表示为 F X F Y F_XF_Y FXFY,( x → y → x \boldsymbol{x}\rightarrow \boldsymbol{y}\rightarrow \boldsymbol{x} x→y→x)
判别器:
-
D X D_X DX:用于判别 x \boldsymbol{x} x和 y x \boldsymbol{y}_x yx
-
D Y D_Y DY:用于判别 y \boldsymbol{y} y和 x y \boldsymbol{x}_y xy
缺失区域编码
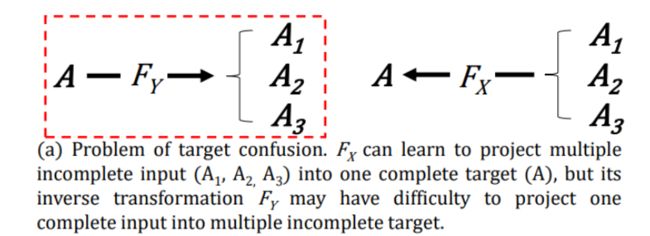
如图(a)所示,当建立从多个缺失形状(例如 A 1 A_1 A1、 A 2 A_2 A2和 A 3 A_3 A3)到一个完整形状(例如 A A A)的形状对应关系时,会出现目标混淆的问题(target confusion problem)。即仅通过普通深度神经网络 F Y F_Y FY将一个完整输入完全映射到多个不同的缺失目标,会导致目标混淆。
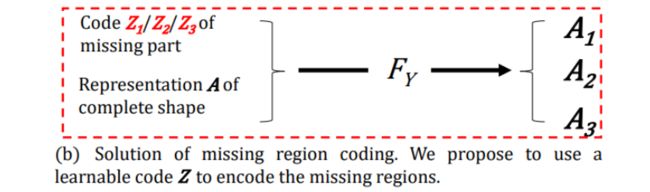
为了解决这个问题,Cycle4Completion使用了可学习缺失区域编码来将缺失形状转换为完整形状,如图(b)所示。缺失形状的表示可以分解为两部分:一部分是对应完整形状的表示 A A A,另一部分是编码缺失区域的编码 Z Z Z。
从缺失形状预测完整形状时,仅考虑表示 A A A。而从完整形状预测缺失形状时,则同时考虑完整形状的表示 A A A和编码 Z Z Z。可学习的缺失区域编码 Z Z Z可以帮助网络明确哪个缺失形状是当前转换的目标,并缓解目标混淆问题。因此,转换网络 F Y F_Y FY将根据编码 Z Z Z,学习将一个完整的输入映射到指定不缺失目标。
用于学习潜在空间的编码器-解码器
两个自编码器分别学习缺失和完整形状的潜在表示空间。
定义点云 P 1 \mathcal{P_1} P1和 P 2 \mathcal{P_2} P2的Chamfer距离为

自编码器的重建损失为:
循环变换
(1)缺失循环转换:
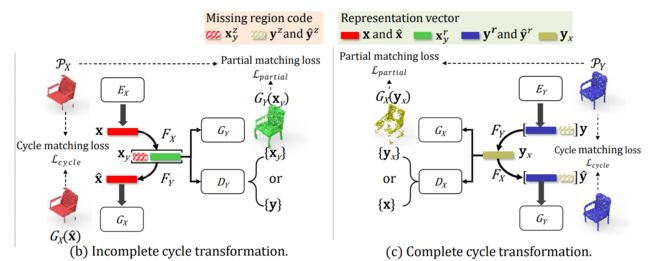
图(b)中,当 x \boldsymbol{x} x 由 F X F_X FX从缺失域转换到完整域的 x y \boldsymbol{x}_y xy时,其中包含缺失区域编码 x y z \boldsymbol{x}_y^z xyz和完整形状表示 x y r \boldsymbol{x}_y^r xyr。故 x y \boldsymbol{x}_y xy可以表示为: x y = [ x y r : x y z ] \boldsymbol{x}_y=[\boldsymbol{x}_y^r: \boldsymbol{x}_y^z] xy=[xyr:xyz](":"表示连接操作)
完整的形状由 x y r \boldsymbol{x}_y^r xyr输入 G Y G_Y GY生成: G Y ( x y r ) G_Y(\boldsymbol{x}_y^r) GY(xyr)。
判别器 D Y D_Y DY判别 x y r \boldsymbol{x}_y^r xyr和 y \boldsymbol{y} y
为了在转换过程中建立形状一致性, x y \boldsymbol{x}_y xy被 F Y F_Y FY转换回缺失域,表示为 x ^ \hat{\boldsymbol{x}} x^。然后使用 G X G_X GX得到循环重建形状,表示为 G X ( x ^ ) G_X(\hat{\boldsymbol{x}}) GX(x^)
(2)完整循环转换
图(c)中, E Y E_Y EY直接预测完整形状的潜在表示 y r \boldsymbol{y}^r yr。为了预测缺失的形状,从[0,1]的均匀分布中采样得到缺失区域编码 y z \boldsymbol{y}^z yz,并将其与 y r \boldsymbol{y}^r yr连接起来 y = [ y r : y z ] \boldsymbol{y}=[\boldsymbol{y}^r:\boldsymbol{y}^z] y=[yr:yz]。
然后,转换网络 F Y F_Y FY将 y \boldsymbol{y} y转换到缺失域,得到 y x \boldsymbol{y}_x yx。
与缺失循环变换类似,缺失形状是 y x \boldsymbol{y}_x yx输入 G X G_X GX得到的,表示为 G X ( y x ) G_X(\boldsymbol{y}_x) GX(yx)
判别器 D X D_X DX判别 y x \boldsymbol{y}_x yx和 x \boldsymbol{x} x。
根据缺失循环变换的逆方向,通过 G Y ( ) G_Y() GY()预测重构形状 G Y ( y ^ ) G_Y(\hat{\boldsymbol{y}}) GY(y^),其中 y ^ = F X ( y x ) \hat{\boldsymbol{y}}=F_X(\boldsymbol{y}_x) y^=FX(yx),建立完整循环变换循环的形状一致性。
与 y \boldsymbol{y} y相同地, y ^ \hat{\boldsymbol{y}} y^也由完整表示 y ^ r \hat{\boldsymbol{y}}^r y^r和缺失区域编码 y ^ z \hat{\boldsymbol{y}}^z y^z组成。
编码匹配损失(Code matching Loss)
从均匀分布中采样缺失区域码 y z \boldsymbol{y}^z yz,是为了从当前完整输入 P Y \mathcal{P}_Y PY创建缺失区域。当形状 P Y \mathcal{P}_Y PY在 F Y F_Y FY和 F X F_X FX之间循环后,变换网络 F Y F X F_YF_X FYFX将预测得到新的缺失区域编码 y ^ z \hat{\boldsymbol{y}}_z y^z。因为 y z \boldsymbol{y}^z yz和 y ^ z \hat{\boldsymbol{y}}_z y^z都对应于相同的缺失形状,所以这两个编码表示应该相等。因此,使用 y z \boldsymbol{y}^z yz和 y ^ z \hat{\boldsymbol{y}}_z y^z之间的欧氏距离作为编码跟踪损失,表示为:
循环匹配损失
循环匹配损失是为了将循环重建 G Y ( y ^ ) / G X ( x ^ ) G_Y(\hat{\boldsymbol{y}})/G_X(\hat{\boldsymbol{x}}) GY(y^)/GX(x^)的形状匹配到
它们相应的输入 P Y / P X \mathcal{P}_Y/\mathcal{P}_X PY/PX,实现在整个转换过程中应保持形状一致性。
特别地,定义 P Y / P X \mathcal{P}_Y/\mathcal{P}_X PY/PX和 G Y ( y ^ ) / G X ( x ^ ) G_Y(\hat{\boldsymbol{y}})/G_X(\hat{\boldsymbol{x}}) GY(y^)/GX(x^)之间的Chamfer距离为 L C D ( P X ⇋ G X ( x ^ ) ) \mathcal{L}_{\mathrm{CD}}\left(\mathcal{P}_{X} \leftrightharpoons G_{X}(\hat{\mathbf{x}})\right) LCD(PX⇋GX(x^))和
L C D ( P Y ⇋ G Y ( y ^ ) ) \mathcal{L}_{\mathrm{CD}}\left(\mathcal{P}_{Y} \leftrightharpoons G_{Y}(\hat{\mathbf{y}})\right) LCD(PY⇋GY(y^))
然后,将传输网络 F X F_X FX和 F Y F_Y FY的循环匹配损失表示为:

部分匹配损失(Partial matching loss)
部分匹配损失是一种方向约束,其目的是在不进行反向匹配的情况下,将一个形状匹配到另一个形状。
将两个点云 P 1 \mathcal{P}_1 P1和 P 2 \mathcal{P}_2 P2之间的部分Chamfer距离定义为:
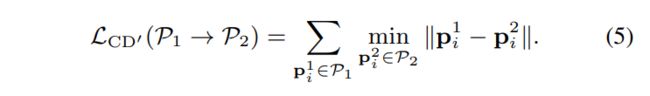
这是一个仅要求 P 2 \mathcal{P}_2 P2的形状与 P 1 \mathcal{P}_1 P1的形状部分匹配的约束。
在图(b)的缺失循环中,有: L C D ′ ( P X → G Y ( x y r ) ) \mathcal{L}_{\mathrm{CD}^{\prime}}\left(\mathcal{P}_{X} \rightarrow G_{Y}\left(\mathbf{x}_{y}^{r}\right)\right) LCD′(PX→GY(xyr))
图(c)中完整循环中,有: L C D ′ ( G X ( y x ) → P Y ) \mathcal{L}_{\mathrm{CD}^{\prime}}\left(G_{X}\left(\mathbf{y}_{x}\right) \rightarrow \mathcal{P}_{Y}\right) LCD′(GX(yx)→PY)
注意,上述两个部分Chamfer距离的方向总是从缺失形状指向完整形状,这保证了缺失形状能够部分匹配完整形状,无论它是预测的 G X ( y x ) G_{X}\left(\mathbf{y}_{x}\right) GX(yx)还是真实数据 P X \mathcal{P}_{X} PX。部分匹配损失定义为:
对抗损失(Adversarial loss)
为了进一步弥合完整和缺失形状的潜在表示,采用对抗式学习框架作为无配对约束。
具体来说,使用两个鉴别器 D X D_X DX和 D Y D_Y DY分别区分缺失域和完整域中的真表示和假表示。缺失域中的 D X D_X DX区分真实的潜在表示 { x } \{\boldsymbol{x}\} {x}和虚假的潜在表示 { y x } \{\boldsymbol{y}_x\} {yx};同样地, D Y D_Y DY则在完整域中判别 y {\boldsymbol{y}} y和 { x y } \{\boldsymbol{x}_y\} {xy}。为了稳定训练,Cycle4Completion使用了WGAN-GP。 D X D_X DX的损失公式为:
生成器 F X , F Y {F_X,F_Y} FX,FY和鉴别器 D X , D Y {D_X,D_Y} DX,DY的最终对抗损失如下所示
训练策略
Θ D \Theta_{D} ΘD: { D X , D Y } \{D_X,D_Y\} {DX,DY}的参数
Θ A E \Theta_{AE} ΘAE: { E X , G X , E Y , G Y } \{E_X,G_X,E_Y,G_Y\} {EX,GX,EY,GY}的参数
Θ F \Theta_{F} ΘF: { F X , F Y } \{F_X,F_Y\} {FX,FY}的参数
L G ( Θ A E , Θ F , Θ D ) \mathcal{L}_G(\Theta_{AE},\Theta_F,\Theta_D) LG(ΘAE,ΘF,ΘD)表示由自编码器(auto-encoder), 转换网络(transferring network)和 判别器(discriminator)来计算 L G \mathcal{L}_G LG
梯度下降优化参数:
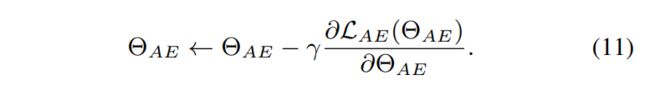
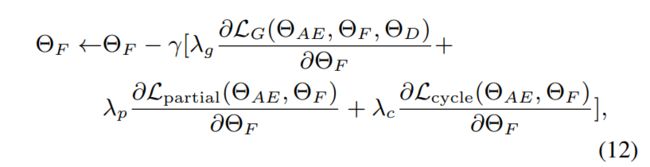
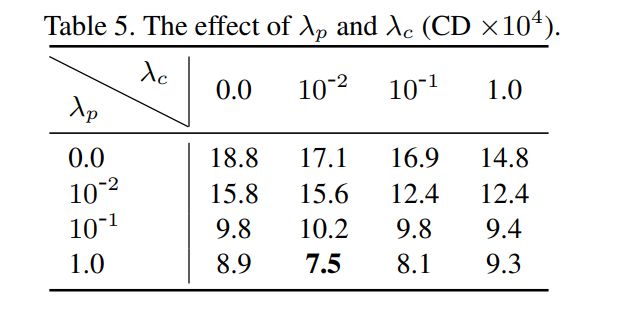
实验中, λ g = 1 , λ c = 0.01 , λ p = 1 \lambda_g=1,\lambda_c=0.01,\lambda_p=1 λg=1,λc=0.01,λp=1
注意,训练 L G \mathcal{L}_G LG和 L p a r t i a l \mathcal{L}_{partial} Lpartial时, Θ A E \Theta_{AE} ΘAE的参数将被固定。原因是 L G \mathcal{L}_G LG和 L p a r t i a l \mathcal{L}_{partial} Lpartial都是两个域转换过程的约束,而这两个自编码器的目的是学习一个域潜在的表示空间,而不是在完整域和缺失域之间传递特征。
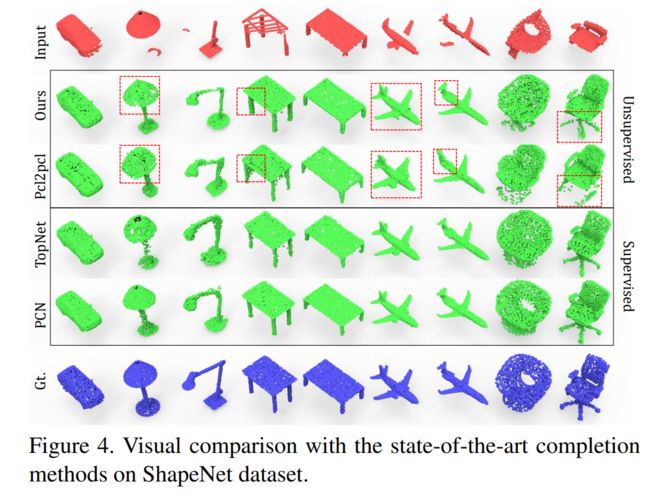
实验
ShapeNet训练后的模型直接用域KITTI数据集
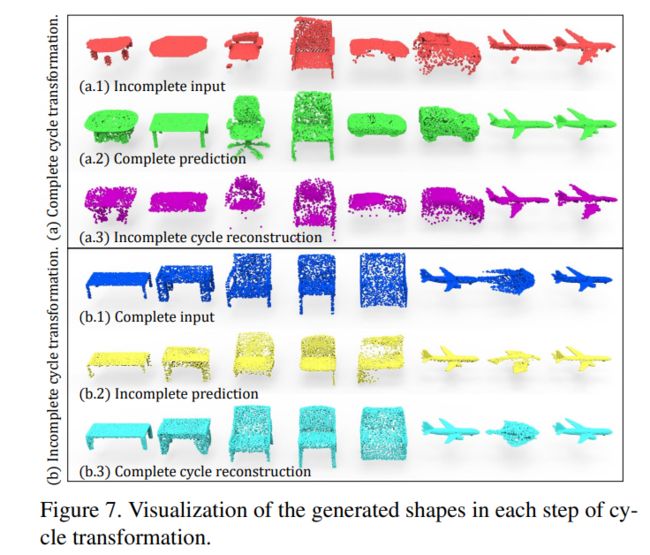
完整循环转换的可视化分析
潜在空间可视化分析
w/ 是with
w/o 是without
λ c \lambda_c λc and λ p \lambda_p λp的影响
附:Chamfer距离
其中 P 1 \mathcal{P}_1 P1和 P 2 \mathcal{P}_2 P2为点集。
第一项表示对于 P 1 \mathcal{P}_1 P1中每一点 p i 1 p^1_i pi1,找 P 2 \mathcal{P}_2 P2中与 p i 1 p^1_i pi1距离最小的点 p i 2 p^2_i pi2。然后求所有 ∣ ∣ p i 1 − p i 2 ∣ ∣ ||p^1_i-p^2_i|| ∣∣pi1−pi2∣∣之和。
第二项表示对于 P 2 \mathcal{P}_2 P2中每一点 p i 2 p^2_i pi2,找 P 1 \mathcal{P}_1 P1中与 p i 2 p^2_i pi2距离最小的点 p i 1 p^1_i pi1。然后求所有 ∣ ∣ p i 2 − p i 1 ∣ ∣ ||p^2_i-p^1_i|| ∣∣pi2−pi1∣∣之和。