【GNN笔记】Graph Transform Network(八)
视频链接:《【图神经网络】GNN从入门到精通》
GTN:基于异构图,进行任务转换的方法
HAN 通过将异构图转换为由元路径 构造的齐次图来学习图表示学习。但是,这些方法由领域专家手动选择元路径 ,因此可能无法捕获每个问题的所有有意义的关系。同样,元路径的选择也会显着影响
性能。与这些方法不同,我们的Graph Transformer Networks可以在异构图上运行并为任务转换图,同时以端到端的方式学习转换图上的节点的表示形式。
在本文中,我们提出了能够生成新图结构的Graph Transformer Network(GTN),其中包括识别原始图上未连接节点之间的有用连接,同时在端到端学习新图上的有效节点表示形式。
一定义
1.1 异构图的邻接矩阵
增添的概念:节点类型的集合,连类型的集合
并以ACM网址的文献集合为案例。

1.2 节点的特征构建
同样以ACM数据集为例,其含有节点3种类型:Paper,Author,Subject.对于每种节点如何用特征表示呢?在前面我们看到总的特征表示 X ∈ R N × D X\in \R^{N\times D} X∈RN×D,可以获得提示:对每种类型的节点的特征表示要求维度一致。统一的尺度方便我们后续的model操作。

注意到:这里的组合方式是可以根据任务来自定义的:max_pooling,mean,min,等等。
1.3 分块矩阵的物理含义
二、算法流程
2.1 多组meta-path
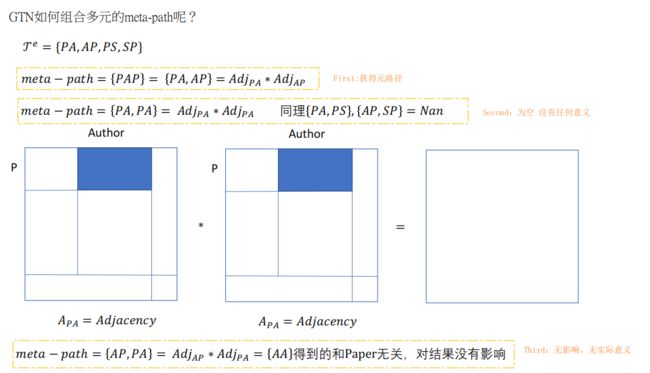
T e = { P A , A P , P S , S P } \mathcal{T}^e= \{PA, AP, PS, SP\} Te={PA,AP,PS,SP},会产生的 meta-path 为:
- PAP=PA*AP,获得矩阵的shape=[P,P]=[3025,3025]
- PAS=PA*AS,获得矩阵的shape=[P,S]=[3025,56]
- APA=AP*PA,获得矩阵的shape=[A,A]=[5835,5835]
- APS=AP*PS,获得矩阵的shape=[A,S]=[5835,56]
因此,结合1.3节种的图片,包含所有类型的邻接矩阵 A ~ \tilde{A} A~,通过矩阵乘法,可以获得所有的 元路径 。
2.2 单通道的生成meta-path
Input:
A ∈ R N × N × 4 A \in R^{N\times N \times 4} A∈RN×N×4:是根据4种类型的连边,获得的节点的点边关系矩阵。为了方便计算,保持同一尺寸。
W Φ 1 , W Φ 2 ∈ R 4 W^1_{\Phi},W^2_{\Phi} \in R^{4} WΦ1,WΦ2∈R4 :是可学习的参数
Model:
Output: A 1 = Q 1 × Q 2 A1=Q1\times Q2 A1=Q1×Q2 ,矩阵乘法。完成了
注释:
- 《一分钟理解softmax函数(超简单)》
- 俗话讲,A具有4个channel,对于每个channel对应一种类型的edge.A包含N个节点(所有类型),对于不同类型的边给一个权重系数即 α 1 , . . , α 4 \alpha_1,..,\alpha_4 α1,..,α4,然后通过加法将所有类型的边合并到同一图中 Q 1 Q_1 Q1,再给一个权重系数可以获得另一个矩阵 Q 2 Q_2 Q2。 Q 1 , Q 2 Q_1,Q_2 Q1,Q2都包含节点中所有类型的边的信息,再根据矩阵乘法可以获得元路径的思想,由此可以得到元路径包含的信息矩阵 A 1 = Q 1 × Q 2 A^1=Q1 \times Q^2 A1=Q1×Q2.
2.3 多通道:
Input:
A ∈ R N × N × C 1 A \in R^{N\times N \times C1} A∈RN×N×C1
W ∈ R C 1 × C 2 W\in R^{C1\times C2} W∈RC1×C2,可学习参数.C1是A的通道数=边的种类数,C2是新的通道数。
Model:
如上:A3包含的路径长度为4的meta-path.

1–>C2 多通道的作用 :如图片中紫色部分。
解惑:

2.4 效果
代码解读
三、main.py文件
3.1 参数
| 变量 | 类型 | 值 | help |
|---|---|---|---|
| dataset | str | 数据集名称 | |
| epoch | int | 40 | 训练轮次 |
| node_dim | int | 64 | 节点维度? |
| num_channels | int | 2 | 通道数目,conv的输出通道 |
| lr | float | 0.005 | 学习率 |
| weight_decay | float | 0.001 | 权重衰减,L2 reg? |
| num_layers | int | 2 | layer的个数 |
| norm | str | true | 是否归一化 ?为什么不是bool |
| adaptive_lr | str | false | 是否采取学习率 |
3.2 读取并查看dataset
-
node_feature.shape :(8994, 1902)。num_nodes=8994
-
edges:包含4个type=scipy.sparse.csr.csr_matrix的且shape=(8994,8994)的 稀疏矩阵组合
-
labels:包含训练集(600,2)、验证集(300,2)和 测试集(2125,2)的标签数据。2种第一个表示数据的index,第二个表示label.且label有3种分类,记作:0,1,2。
-
edges中矩阵合并
将edges中的4个稀疏矩阵通过todense()转化为稠密矩阵,使用.unsqueeze(-1)在尾部添加新的数轴,使用torch.cat(,dim=-1)在新数轴上循环合并4个矩阵。
3.3 实例化:GTN\optimizer\lossfunction
model = GTN(num_edge=A.shape[-1], # edge类别的数量; 还有一个单位阵;4+1=5
num_channels=num_channels, # 2
w_in = node_features.shape[1], # ACM:1902
w_out = node_dim, # 64
num_class=num_classes, # 3
num_layers=num_layers, # GTLayer 2
norm=norm) # True
if adaptive_lr == 'false':
optimizer = torch.optim.Adam(model.parameters(), lr=0.005, weight_decay=0.001)
else:
optimizer = torch.optim.Adam([{'params':model.weight},
{'params':model.linear1.parameters()},
{'params':model.linear2.parameters()},
{"params":model.layers.parameters(), "lr":0.5}
], lr=0.005, weight_decay=0.001)
loss = nn.CrossEntropyLoss()
注释:
- 这里采用了2中优化方法,没看明白。建议文章:《Optimization(最优化)》
- 损失函数采用了:交叉熵的方法,《原理理解》, 《谈Cross Entropy Loss》,
CLASS torch.nn.CrossEntropyLoss(weight: Optional[torch.Tensor] = None, size_average=None, ignore_index: int = -100, reduce=None, reduction: str = 'mean')
3.4 model的Train & Valid
- 初始值设置
- 循环for 训练
### 1. set optimizer lr
for param_group in optimizer.param_groups:
if param_group['lr'] > 0.005:
param_group['lr'] = param_group['lr'] * 0.9
print('Epoch: ',i+1)
#### 2. 设置0梯度并切换训练模式进行训练
model.zero_grad()
model.train() # A:[8994, 8994, 5],5个edgeType; node_features;
loss,y_train,Ws = model(A, node_features, train_node, train_target)
### 3. 根据model的output,并计算train_f1
train_f1 = torch.mean(f1_score(torch.argmax(y_train.detach(),dim=1), train_target, num_classes=num_classes)).cpu().numpy()
print('Train - Loss: {}, Macro_F1: {}'.format(loss.detach().cpu().numpy(), train_f1))
### 4. 优化参数
loss.backward()
optimizer.step()
### 5. 切换到评估模式
model.eval()
### 6. 在梯度不变的空间下计算val_f1,test_f1
with torch.no_grad():
val_loss, y_valid,_ = model.forward(A, node_features, valid_node, valid_target)
val_f1 = torch.mean(f1_score(torch.argmax(y_valid,dim=1), valid_target, num_classes=num_classes)).cpu().numpy()
print('Valid - Loss: {}, Macro_F1: {}'.format(val_loss.detach().cpu().numpy(), val_f1))
test_loss, y_test,W = model.forward(A, node_features, test_node, test_target)
test_f1 = torch.mean(f1_score(torch.argmax(y_test,dim=1), test_target, num_classes=num_classes)).cpu().numpy()
print('Test - Loss: {}, Macro_F1: {}\n'.format(test_loss.detach().cpu().numpy(), test_f1))
### 7. 并录当下训练的最优结果
if val_f1 > best_val_f1:
best_val_loss = val_loss.detach().cpu().numpy()
best_test_loss = test_loss.detach().cpu().numpy()
best_train_loss = loss.detach().cpu().numpy()
best_train_f1 = train_f1
best_val_f1 = val_f1
best_test_f1 = test_f1
- 打印三个最优的train_f1,val_f1,test_f1
四、model.py文件
4.1 GTconv
这个模块相当于model中的可学习参数 W 1 , W 2 , . . . W1,W2,... W1,W2,...,然后进行softmax函数。
4.1.1 def
- 设置卷积核:self.weight(5,2,1,1)
- 设置偏置参数:self.bias
- 调用self.reset_parameter()函数进行参数初始化
A. self.weight采用常数0.1进行初始化
B. self.bias 如果不为None,进行初始化
def __init__(self, in_channels, out_channels):
super(GTConv, self).__init__()
self.in_channels = in_channels # 5
self.out_channels = out_channels # 2
self.weight = nn.Parameter(torch.Tensor(out_channels,in_channels,1,1)) #
self.bias = None
self.reset_parameters()
注释:
4. self.reset_parameters()

5. nn.init._calculate_fan_in_and_fan_out(self.weight):计算weight的fan_in和fan_out
6. 《理解fan_in和fan_out》
7. 《PyTorch模型参数初始化》中案例讲解。
4.1.2 forward
Input:
A: shape=(1,5,8944,8944) ,1=out_channel,5=in_channel
parameter:
self.weight:[out_channel,in_channel,1,1] ,其中卷积核大小为1*1
- 对weight(conv)进行softmax得到W:[2,5,1,1]–>[2,5,1,1]
- 对每个节点在每个edgeType上进行[2, 5, 1, 1]的卷积操作;
A ∗ W A*W A∗W:[1,5,8944,8944]*[2,5,1,1]–>[2,5,8944,8944]- 对每个edgeType进行加权求和
Q = s u m ( A ∗ W , d i m = 1 ) Q=sum(A*W,dim=1) Q=sum(A∗W,dim=1): [2,5,8944,8944]–>[2,8944,8944]
output:
Q:[out_channel, N, N]=[2, 8944,8944]
def forward(self, A):
# self.weight:带有channel的conv;
# F.softmax(self.weight, dim=1) 对self.weight做softmax:[2, 5, 1, 1]
# A: [1, 5, 8994, 8994]:带有edgeType的邻接矩阵
# [1, 5, 8994, 8994]*[2, 5, 1, 1] => [2, 5, 8994, 8994]
# sum:[2, 8994, 8994]
A = torch.sum(A*F.softmax(self.weight, dim=1), dim=1)
return A
4.2 GTlayer
根据公式 A ( l ) = Q 1 ∗ Q 2 ∗ ⋯ ∗ Q l A^{(l)}=Q1 * Q2 *\cdots * Ql A(l)=Q1∗Q2∗⋯∗Ql.值得注意的是 l ≥ 2 l \geq 2 l≥2 。因此,在第一层需要定义两个GTconv,而后每增加一层的时候只需要再定义一个GTconv即可。因此通过first来控制每次增加1个或着2个GTconv。
4.2.1 def
def __init__(self, in_channels, out_channels, first=True):
super(GTLayer, self).__init__()
self.in_channels = in_channels #5
self.out_channels = out_channels #2 # 1x1卷积的channel数量
self.first = first
if self.first == True:
self.conv1 = GTConv(in_channels, out_channels) # W1
self.conv2 = GTConv(in_channels, out_channels) # W2
else:
self.conv1 = GTConv(in_channels, out_channels)
4.2.2 forward
Input:
A : ( 8944 , 8944 , 5 ) A:(8944,8944,5) A:(8944,8944,5),组合矩阵
H:默认为None,否则
Flow:
if self.first==True. 下面的
- Q.shape =[out_channel, N, N]=[2, 8944, 8944]
- Q.weight.shape=[out_channel, in_channel, 1, 1 ]=[2,5,1,1]
Output:
H: Q 1 ∗ Q 2 Q1*Q2 Q1∗Q2.shape=[2, 8944,8944]
W=[W1, W2] ,W1.shape =[2,5, 1,1]
if self.first==False
Output:
H : H − ∗ Q 3 H: H_{-} *Q3 H:H−∗Q3.shape=[2, 8944,8944]
W=[W3] ,W3.shape=[2,5,1,1]
4.3 GTN
根据公式 A ( l ) = Q 1 ∗ Q 2 ∗ ⋯ ∗ Q l A^{(l)}=Q1 * Q2 *\cdots * Ql A(l)=Q1∗Q2∗⋯∗Ql,当我们获取长度为l的meta-path的时候, 需要 l l l个GTconv。根据4.2节可知,每次增加的GTconv由GTlayer控制。根据 l l l,可知要堆叠 l − 1 l-1 l−1个GTlayer。
其次,搭建GCN层获得节点表示。
最后,搭建2层全连接层获得节点最终的分类。
4.3.1 def
def __init__(self, num_edge, num_channels, w_in, w_out, num_class,num_layers,norm):
super(GTN, self).__init__()
self.num_edge = num_edge # 5
self.num_channels = num_channels #2
self.w_in = w_in # 1902
self.w_out = w_out # 64
self.num_class = num_class # 3
self.num_layers = num_layers # 2
self.is_norm = norm # true
layers = []
for i in range(num_layers): # layers多个GTLayer组成的; 多头channels
if i == 0:
layers.append(GTLayer(num_edge, num_channels, first=True)) # 第一个GT层,edge类别构建的矩阵
else:
layers.append(GTLayer(num_edge, num_channels, first=False))
self.layers = nn.ModuleList(layers)
self.weight = nn.Parameter(torch.Tensor(w_in, w_out)) # GCN层的weight
self.bias = nn.Parameter(torch.Tensor(w_out)) # GCN层的bias
self.loss = nn.CrossEntropyLoss()
self.linear1 = nn.Linear(self.w_out*self.num_channels, self.w_out)
self.linear2 = nn.Linear(self.w_out, self.num_class)
self.reset_parameters()
注释:
- self.weight和self.bias是单层GCN的权重和偏置。因此,self.weight.shape=(1902,64).因为是单层所以可通过计算: Y = A ∗ X ∗ W + b Y=A*X*W+b Y=A∗X∗W+b即可。
- self.linear1: (64*2, 64).本质上是对经过GCN层获得每个channel的节点表示的拼接。
- self.linear2: (64,3) . 本质上根据拼接后的节点表示进行节点的分类。
4.3.2 forward
Input:
A : ( 8944 , 8944 , 5 ) A:(8944,8944,5) A:(8944,8944,5),组合矩阵
X : ( 8944 , 1902 ) X:(8944,1902) X:(8944,1902), 节点的特征表示
target_X:(L,),L表示集合(train\val\test)的长度,表示index
target:(L,), L同理,表示label
Flow:
- A–升维转置–>A(1,5, 8944,8944):1表示output_channel的位置
- i=0:进入self.layers[0]
- (conv1): GTConv(A)
- (conv2): GTConv(A)
- 返回 H, W: 当前H=Q1*Q2, W=[W1,W2]
- Ws.append(W):当前 Ws=[W1,W2]
- i=1: 进入self.layers[1]
- H–self.normalization–>norm(H)
- (conv3):GTConv(A)
- 返回H,W:当前H=norm(H)*Q3. W=[W3]
- Ws.append(W):当前 Ws=[W1,W2,W3]
- i =0 :进行第一个channel,进行GCN,X_=GCN(X, H[0])
- i=1: 进行第二个channel,进行GCN, X_tmp=GCN(X,H[1])
X_=cat([X_,X_tmp],dim=1) node present 的拼接 - 经历第一个全连接层X_=self.linear1(X_)
- 经历第二个全连接层Y=self.linear2(X_)
- 采用交叉熵计算损失函数,loss=loss(y,target)
- return : loss, y, Ws
4.3.3 self.normalization
- H:[2, 8944, 8944]
- H0=H[0,:,:], shape=(8944,8944) -->dim=0处升维
- H1=H[0,:,:], shape=(8944,8944)–>Norm归一化–>dim=0处升维
- cat([H0,H1],dim=0)合并
def normalization(self, H):
for i in range(self.num_channels):
if i==0:
H_ = self.norm(H[i,:,:]).unsqueeze(0) # Q1
else:
H_ = torch.cat((H_,self.norm(H[i,:,:]).unsqueeze(0)), dim=0) # Q2
return H_
- H 转置
- add==False:因为自环没有意义,去掉自环
建立一个主对角线元素为0其余为1的bool矩阵 E。
H*E:去自环 - add ==True:去掉自环,添加单位矩阵(为保留图本身的性质)。
- D − 1 H D^{-1}H D−1H:按行求和,再除以和
- debug:“inf”的情况(因为存在除法)
- 矩阵内积,进行归一化
- H 转置
整体而言,相当于对矩阵的列进行归一化。
def norm(self, H, add=False):
H = H.t() # t
if add == False:
H = H*((torch.eye(H.shape[0])==0).type(torch.FloatTensor)) # 建立一个对角阵; 除了自身节点,对应位置相乘。Degree(排除本身)
else:
H = H*((torch.eye(H.shape[0])==0).type(torch.FloatTensor)) + torch.eye(H.shape[0]).type(torch.FloatTensor)
deg = torch.sum(H, dim=1) # 按行求和, 即每个节点的dgree的和
deg_inv = deg.pow(-1) # deg-1 归一化操作
deg_inv[deg_inv == float('inf')] = 0
deg_inv = deg_inv*torch.eye(H.shape[0]).type(torch.FloatTensor) # 转换成n*n的矩阵
H = torch.mm(deg_inv,H) # 矩阵内积
H = H.t()
return H