第十一届蓝桥杯python大学组国赛真题（部分题解）

第十一届蓝桥杯python大学组国赛真题

试题 A: 美丽的 2

【问题描述】
小蓝特别喜欢 2，今年是公元 2020 年，他特别高兴。
他很好奇，在公元 1 年到公元 2020 年（包含）中，有多少个年份的数位中包含数字 2？

if __name__ == '__main__':
    count = 0
    for i in range(1,2021):
        if '2' in str(i):
            count += 1
    print(count)

试题 B: 合数个数

【问题描述】
一个数如果除了 1 和自己还有其他约数，则称为一个合数。例如：1, 2, 3不是合数，4, 6 是合数。
请问从 1 到 2020 一共有多少个合数。

if __name__ == '__main__':
    count = 0
    # temp = 0
    for i in range(1,2021):
        temp = 0
        for j in range(2,i//2+1):
            if i%j == 0:
                count += 1
                break
    print(count)

试题 C: 阶乘约数

【问题描述】
定义阶乘 n! = 1 × 2 × 3 × · · · × n。
请问 100! （100 的阶乘）有多少个约数。

思路：惟一分解定理

约数个数 = (a1 + 1)(a2 + 1)……(ak + 1)

也就是说我们需要求出100！阶乘的所有质数；但是太大太多，一定是不好求的；所以我们改为求每个因数的质数，然后记录数量就可以。

if __name__ == '__main__':
    dic = {}
    sums = 1
    for i in range(2,100):
        pri = True
        for j in range(2,i//2+1):
            if i%j == 0:
                pri = False
                break
        if pri:
            dic[i] = 1

    for i in range(2,101):
        temp = i
        for j in dic.keys():
            while temp % j == 0:
                temp //= j
                dic[j] += 1

    for values in dic.values():
        sums *= values
    print(sums)
#结果
39001250856960000

试题 D: 本质上升序列

【问题描述】
小蓝特别喜欢单调递增的事物。
在一个字符串中，如果取出若干个字符，将这些字符按照在字符串中的顺序排列后是单调递增的，则成为这个字符串中的一个单调递增子序列。
例如，在字符串 lanqiao 中，如果取出字符 n 和 q，则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现，有些子序列虽然位置不同，但是字符序列是一样的，例如取第二个字符和最后一个字符可以取到 ao，取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串，小蓝想知道，本质不同的递增子序列有多少个？
例如，对于字符串 lanqiao，本质不同的递增子序列有 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、anq、lno、ano、aio。
请问对于以下字符串（共 200 个小写英文字母，分四行显示）：（如果你把以下文字复制到文本文件中，请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt，内容与下面的文本相同）

tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl

本质不同的递增子序列有多少个？

试题 E: 玩具蛇

【问题描述】
小蓝有一条玩具蛇，一共有 16 节，上面标着数字 1 至 16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4 的方格盒子，用于存放玩具蛇，盒子的方格上依次标着字母 A 到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现，有很多种方案可以将玩具蛇放进去。
下图给出了两种方案：

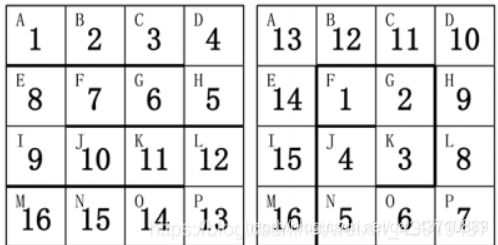
请帮小蓝计算一下，总共有多少种不同的方案。如果两个方案中，存在玩具蛇的某一节放在了盒子的不同格子里，则认为是不同的方案。

试题 F: 天干地支

【问题描述】
古代中国使用天干地支来记录当前的年份。
天干一共有十个，分别为：甲（jiǎ）、乙（yǐ）、丙（bǐng）、丁（dīng）、戊
（wù）、己（jǐ）、庚（gēng）、辛（xīn）、壬（rén）、癸（guǐ）。
地支一共有十二个，分别为：子（zǐ）、丑（chǒu）、寅（yín）、卯（mǎo）、辰（chén）、巳（sì）、午（wǔ）、未（wèi）、申（shēn）、酉（yǒu）、戌（xū）、亥（hài）。
将天干和地支连起来，就组成了一个天干地支的年份，例如：甲子。2020 年是庚子年。
每过一年，天干和地支都会移动到下一个。例如 2021 年是辛丑年。
每过 60 年，天干会循环 6 轮，地支会循环 5 轮，所以天干地支纪年每 60年轮回一次。例如 1900 年，1960 年，2020 年都是庚子年。
给定一个公元纪年的年份，请输出这一年的天干地支年份。
【输入格式】
输入一行包含一个正整数，表示公元年份。
【输出格式】
输出一个拼音，表示天干地支的年份，天干和地支都用小写拼音表示（不表示声调），之间不要加入任何多余的字符。
【样例输入】
2020
【样例输出】
gengzi
【评测用例规模与约定】
对于所有评测用例，输入的公元年份为不超过 9999 的正整数。

# 2020 年是庚子
#以2020，1960,1900任意一个为基准
if __name__ == '__main__':
    t = ["", "xin", "ren", "gui", "jia", "yi", "bing", "ding", "wu", "ji", "geng"]
    d = ["", "you", "xu", "hai", "zi", "chou", "yin", "mao", "chen", "si", "wu", "wei", "shen"]
    a = 10
    b = 4
    year = int(input())

    if year-2020 >=0:
        for i in range(year-2020):
            a = (a+1)%10
            b = (b+1)%12
    else:
        for i in range(2020-year):
            a += -1 if a>1 else a+8
            print(a)
            b += -1 if b>1 else b+10
            # print(b)
    print(t[a]+d[b])

试题 G: 重复字符串

【问题描述】
如果一个字符串 S 恰好可以由某个字符串重复 K 次得到，我们就称 S 是 K 次重复字串。例如 “abcabcabc” 可以看作是 “abc” 重复 3 次得到，所以“abcabcabc” 是 3 次重复字符串。
同理 “aaaaaa” 既是 2 次重复字符串、又是 3 次重复字符串和 6 次重复字符串。
现在给定一个字符串 S，请你计算最少要修改其中几个字符，可以使 S 变为一个 K 次字符串？

【输入格式】
输入第一行包含一个整数 K。
第二行包含一个只含小写字母的字符串 S。

【输出格式】
输出一个整数代表答案。如果 S 无法修改成 K 次重复字符串，输出 1。

【样例输入】
2
aabbaa

【样例输出】
2

【评测用例规模与约定】
对于所有评测用例，1 ≤ K ≤ 100000, 1 ≤ |S | ≤ 100000。其中 |S | 表示 S 的
长度。

试题 H: 答疑

【问题描述】
有 n 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。
老师可以安排答疑的顺序，同学们要依次进入老师办公室答疑。
一位同学答疑的过程如下：

首先进入办公室，编号为 i 的同学需要 si 毫秒的时间。
然后同学问问题老师解答，编号为 i 的同学需要 ai 毫秒的时间。
答疑完成后，同学很高兴，会在课程群里面发一条消息，需要的时间可以忽略。
最后同学收拾东西离开办公室，需要 ei 毫秒的时间。一般需要 10 秒、
20 秒或 30 秒，即 ei 取值为 10000，20000 或 30000。
一位同学离开办公室后，紧接着下一位同学就可以进入办公室了。
答疑从 0 时刻开始。老师想合理的安排答疑的顺序，使得同学们在课程群
里面发消息的时刻之和最小
【输入格式】
输入第一行包含一个整数 n，表示同学的数量。
接下来 n 行，描述每位同学的时间。其中第 i 行包含三个整数 si, ai, ei，意
义如上所述。
【输出格式】
输出一个整数，表示同学们在课程群里面发消息的时刻之和最小是多少。
【样例输入】
3
10000 10000 10000
20000 50000 20000
30000 20000 30000
【样例输出】
280000
【样例说明】
按照 1, 3, 2 的顺序答疑，发消息的时间分别是 20000, 80000, 180000。
【评测用例规模与约定】
对于 30% 的评测用例，1 ≤ n ≤ 20。
对于 60% 的评测用例，1 ≤ n ≤ 200。
对于所有评测用例，1 ≤ n ≤ 1000，1 ≤ si ≤ 60000，1 ≤ ai ≤ 1000000， ei ∈ {10000, 20000, 30000}，即 ei 一定是 10000、20000、30000 之一。

#思路：啥啥啥，我都不明白这个题为什么会出在H序号上？原本以为上一个同学发消息，下一个同学就可以走了同时上一个同学也在走出教室。
结果：给的示例意思是：

if __name__ == '__main__':
    sums = 0
    temp = 0
    count = int(input())
    re = []
    lst = [list(map(int,input().split())) for i in range(count)]
    for i in range(count):
        re.append([lst[i][0]+lst[i][1],lst[i][2]])
    re.sort()
    print(re)
    for i in range(count):
        if i == 0:
            temp += re[i][0]
            sums += temp
        else:
            temp += re[i][0] + re[i-1][1]
            sums += temp
    print(sums)

题 I: 补给

【问题描述】
小蓝是一个直升飞机驾驶员，他负责给山区的 n 个村庄运送物资。每个月，他都要到每个村庄至少一次，可以多于一次，将村庄需要的物资运送过去。每个村庄都正好有一个直升机场，每两个村庄之间的路程都正好是村庄之间的直线距离。
由于直升机的油箱大小有限，小蓝单次飞行的距离不能超过 D。每个直升机场都有加油站，可以给直升机加满油。每个月，小蓝都是从总部出发，给各个村庄运送完物资后回到总部。如果方便，小蓝中途也可以经过总部来加油。
总部位于编号为 1 的村庄。请问，要完成一个月的任务，小蓝至少要飞行多长距离？

【输出格式】
输出一行，包含一个实数，四舍五入保留正好 2 位小数，表示答案。
【样例输入】
4 10
1 1
5 5
1 5
5 1
【样例输出】
16.00
【样例说明】
四个村庄形成一个正方形的形状。
【样例输入】
4 6
1 1
4 5
8 5
11 1
【样例输出】
28.00
【样例说明】
补给顺序为 1 → 2 → 3 → 4 → 3 → 2 → 1。
【评测用例规模与约定】
对于所有评测用例，1 ≤ n ≤ 20, 1 ≤ xi, yi ≤ 104, 1 ≤ D ≤ 105。

试题 J: 蓝跳跳

【问题描述】
小蓝制作了一个机器人，取名为蓝跳跳，因为这个机器人走路的时候基本
靠跳跃。
蓝跳跳可以跳着走，也可以掉头。蓝跳跳每步跳的距离都必须是整数，每步可以跳不超过 k 的长度。由于蓝跳跳的平衡性设计得不太好，如果连续两次
都是跳跃，而且两次跳跃的距离都至少是 p，则蓝跳跳会摔倒，这是小蓝不愿意看到的。
小蓝接到一个特别的任务，要在一个长为 L 舞台上展示蓝跳跳。小蓝要控制蓝跳跳从舞台的左边走到右边，然后掉头，然后从右边走到左边，然后掉头，然后再从左边走到右边，然后掉头，再从右边走到左边，然后掉头，如此往复。为了让观者不至于太无趣，小蓝决定让蓝跳跳每次用不同的方式来走。小蓝将蓝跳跳每一步跳的距离记录下来，按顺序排成一列，显然这一列数每个都不超过 k 且和是 L。这样走一趟就会出来一列数。如果两列数的长度不同，或者两列数中存在一个位置数值不同，就认为是不同的方案。
请问蓝跳跳在不摔倒的前提下，有多少种不同的方案从舞台一边走到另一边。
【输入格式】
输入一行包含三个整数 k, p, L。
【输出格式】
输出一个整数，表示答案。答案可能很大，请输出答案除以 20201114 的余数。
【样例输入】
3 2 5
【样例输出】
9
【样例说明】
蓝跳跳有以下 9 种跳法：

1+1+1+1+1
1+1+1+2
1+1+2+1
1+2+1+1
2+1+1+1
2+1+2
1+1+3
1+3+1
3+1+1
【样例输入】
5 3 10
【样例输出】
397
【评测用例规模与约定】
对于 30% 的评测用例，1 ≤ p ≤ k ≤ 50，1 ≤ L ≤ 1000。
对于 60% 的评测用例，1 ≤ p ≤ k ≤ 50，1 ≤ L ≤ 109。
对于 80% 的评测用例，1 ≤ p ≤ k ≤ 200，1 ≤ L ≤ 1018。
对于所有评测用例，1 ≤ p ≤ k ≤ 1000，1 ≤ L ≤ 1018。