利用DGL中的消息传递API手搭GCN实现节点分类

1. 前言

前面的两篇文章分别介绍了DGL中的数据格式和消息传递API：

1. 了解DGL中的数据格式
2. 详解DGL中的消息传递API

这篇文章主要利用前面两篇文章的知识来搭建一个GCN。

2. 数据

本篇文章使用Citeseer网络。Citeseer网络是一个引文网络，节点为论文，一共3327篇论文。论文一共分为六类：Agents、AI（人工智能）、DB（数据库）、IR（信息检索）、ML（机器语言）和HCI。如果两篇论文间存在引用关系，那么它们之间就存在链接关系。网络中一共有3327个节点，然后节点的特征维度为3703，这里实际上是去除停用词和在文档中出现频率小于10次的词，整理得到3703个唯一词。

网络加载：

from dgl.data.citation_graph import CiteseerGraphDataset

dataset = CiteseerGraphDataset()
graph = dataset[0]

由于GCN中需要用到节点度，因此处理如下：

features = graph.ndata['feat']
labels = graph.ndata['label']
train_mask = graph.ndata['train_mask']
val_mask = graph.ndata['val_mask']
test_mask = graph.ndata['test_mask']
in_feats = features.shape[1]
n_classes = dataset.num_labels
# 添加自环
graph = dgl.add_self_loop(graph)
# 获取节点的度
deg = graph.in_degrees().float()
norm = torch.pow(deg, -0.5)
norm[torch.isinf(norm)] = 0
graph.ndata['norm'] = norm.unsqueeze(1)
graph.ndata['f'] = features

3. GCN

通过ICLR 2017 | GCN：基于图卷积网络的半监督分类我们知道GCN中的消息传递机制为：

其中$\tilde{A}=A+I_N$，即邻接矩阵在原有基础上加上一个单位矩阵，也即每一个节点都增加一条指向自己的边；$\tilde{D}$为加上自环后的度矩阵；$W^{(l)}$为层权重矩阵；$\sigma (\cdot )$为激活函数，比如ReLU；$H^{(0)}=X$，也就是节点特征矩阵；经过多层卷积后，我们得到了最终的$H^k$，$H^k$即GCN学到的节点的状态向量表示。

可以发现，本文在传统图卷积的基础上做了两点创新：

1. $\tilde{A}=A+I_N$。每个节点强行加上自环，这样节点的状态向量在向前传播过程中就能考虑到自身的特征信息。
2. 对加上自环后的邻接矩阵$\tilde{A}$进行了归一化：${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$。归一化后的邻接矩阵每一行的和都为1。

我们来分析一下GCN中的消息传递机制:

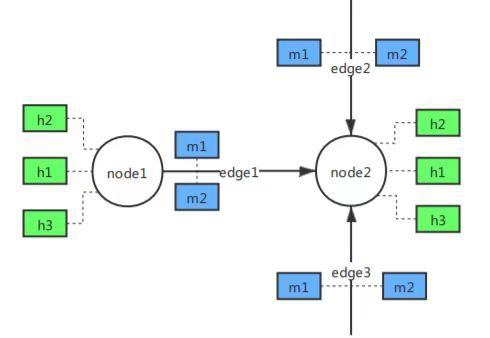
可以发现，目标节点接收源节点的特征(或结合边特征)，最后根据这个特征和自己本身的特征生成新的特征。

DGL实际上已经封装好了GCN，即GraphConv，具体实现原理如下：

即GCN中，节点每次都聚合所有邻居的特征来生成自己新的特征，具体做法是对他们求加权和，而权重为$\frac{1}{c_{ji}}$，而$c_{ji}$为两个节点度开根号的乘积。

因此，基于上述理论，我们搭建的GCNConv如下所示：

def gcn_message_func(edges):
    w = edges.src['norm'] * edges.dst['norm']
    return {'h': edges.src['f'] * w}


def gcn_reduce_func(nodes):
    return {'s': torch.sum(nodes.mailbox['h'], 1)}


class GCNConv(nn.Module):
    def __init__(self, in_feats, out_feats):
        super(GCNConv, self).__init__()
        self.tanh = nn.Tanh()
        self.linear = nn.Linear(in_feats, out_feats)

    def forward(self, g, f):
        g.ndata['f'] = f
        g.update_all(gcn_message_func, gcn_reduce_func)
        g.ndata['f'] = self.linear(g.ndata['f'])
        g.ndata['f'] = self.tanh(g.ndata['f'])
        f = g.ndata.pop('f')
        return f

3.1 消息函数

在这一步中，每条边$v_j->v_i$上的每个源节点$v_j$将自己的特征乘上$c_{ji}$，然后发送到目标节点$v_i$的mailbox中，即：

def gcn_message_func(edges):
    w = edges.src['norm'] * edges.dst['norm']
    return {'h': edges.src['f'] * w}

其中norm为对应节点度的$-\frac{1}{2}$次方。

3.2 聚合函数

目标节点直接将所有源节点发送来的加权特征求和，然后当做自己的特征：

def gcn_reduce_func(nodes):
    return {'s': torch.sum(nodes.mailbox['h'], 1)}

这里mailbox['h']的维度为(batch_size, N, in_feats)，其中N表示这批节点都有N个源节点的特征需要进行聚合，因此我们在这个维度上直接求和。

3.3 更新函数

得到加权后的特征后，再利用一个线性变换和激活函数，得到更新后的节点特征，即：

g.ndata['f'] = self.linear(g.ndata['f'])
g.ndata['f'] = self.tanh(g.ndata['f'])

3.4 模型训练/测试

模型训练：

def train():
    model = GCN(in_feats, 32, n_classes).to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=1e-4)
    loss_function = torch.nn.CrossEntropyLoss().to(device)
    model.train()
    min_epochs = 10
    best_model = None
    min_val_loss = 5
    for epoch in range(50):
        f = model(graph)
        loss = loss_function(f[train_mask], labels[train_mask])
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        # validation
        val_loss = get_val_loss(model)
        if epoch + 1 >= min_epochs and val_loss < min_val_loss:
            min_val_loss = val_loss
            best_model = copy.deepcopy(model)
        print('Epoch: {:3d} train_Loss: {:.5f} val_loss: {:.5f}'.format(epoch, loss.item(), val_loss))
        model.train()

    return best_model

模型测试：

def test(model):
    model.eval()
    _, pred = model(graph).max(dim=1)
    correct = int(pred[test_mask].eq(labels[test_mask]).sum().item())
    acc = correct / int(test_mask.sum())
    print('GCN Accuracy: {:.4f}'.format(acc))