列生成算法原理(单纯形基础)

一 、单纯形法基础

 1.1 定理和推论

定理1： X 是可行域 P 的一个顶点 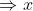 的正分量对应的 A 中的各列是线性独立的。

补充：

（1）

 

 （2）

 *******推论*******：

注： 基可行解对应有解，即列向量之间线性无关（定理1成立）

 （满秩）

由于可能有退化的情况，所以基可行解和顶点不是一一映射：

任给一个基可行解，存在唯一的一个顶点与之对应；对于 P 的一个顶点，可能有多个基可行解与之对应

1.2 单纯形算法

 

则上述线性规划问题就变成：

 

 

 注：1. 检验数为正，说明 reduce cost可以继续下降 ；2. 当所有检验数为正值，reduce cost对于所有为正的x只能继续上升，无法下降，因此达到了最优解

1.3 求基可行解方法

                                                             原始问题标准型

                                                       对约束构造人工变量

此时约束已经变了，目标问题求解也就变了。两种通用的方法就出来了---大M法和两阶段法，一般使用大M法，M是一个充分大的数，目标函数求最大就取减号，求最小就取加号。在这个问题中要有最优解，人工变量就必须取0，（大M作为惩罚因子使得最优解对应的变量一定为“0”，从而消除加入变量的影响）否则，原问题无解。这样就很顺利的得到了一个基可行解，然后代入单纯形算法进行迭代。

1.4 入基变量的选取：

最简单的选取规则就是：目标函数求max,检验数大的为入基变量,目标函数求min,检验数小的为入基变量

1.5 出基变量的选取：

最小比值法选取出基变量，当选取完入基变量  后，取  （将出基变量变为“0”，从而得到入基变量的值，），相应的  做为出基变量置为0，取最小的原则是可以保证  ，防止出现非负变量。（不取最小值，则会使其他变量变为负数，从而违背变量x全为正的约束条件）

借用原作者的图，在进行出基、入基后，使用新基变量使得基变量系数为单位阵（表示线性独立的形式，即一个基变量均由非基变量和常数项b来表示），非基变量系数则使用进行更新，从而重新表达新的变量之间的关系

1.6 几何解释

• 线性规划是一个凸优化问题，局部最优解就是全局最优解。
• 线性规划的解空间是一个n维的凸多面体。最优解在这个凸多面体的某个顶点上。
• 单纯形算法从一个初始顶点开始，不断沿着邻边找更好的顶点。
• 当一个顶点四周没有更好的顶点时，这个顶点就是最优解。

---

二、列生成

  单纯形需要计算所有非基变量的RC。找到最小的那个。当变量个数很多的时候，这一步就成为了算法运行时间瓶颈。

而列生成只要能在每次迭代的时候生成一个或者多个变量，提升优化效果就可以了。由于不需要遍历所有变量，所以一开始就不需要使用所有变量，只需要使用一组能产生初始解的初始变量构成线性优化问题即可。这种只使用部分变量的模型被称为原问题的restricted master problem（RMP）。

每次迭代时，生成一个或多个让reduced cost最小的变量加入RMP。这个生成步骤就是求解子问题。不断加入新变量直到没有小于0的reduced cost的变量时就达到最优解。

下面是单纯形算法与列生成算法简要流程图的对比，可以看到，两者的结构是一样的。

2.1  对偶角度

假设有个很标准的线性规划问题：

那么，它的对偶问题为：

借用经济学方面的话来说，假设原问题的目标是让成本最小，那么对偶就是让收入最大。更确切地讲，是：

• 原问题   ：保证收入不低于某个值的条件下，使成本最小化。
• 对偶问题：保证成本不高于某个值的条件下，使收入最大化。

可以看到，原问题和对偶问题其实就是一个问题：目标净收益最大。只是一个是约束收入优化成本，一个是约束成本优化收入。角度不同而已。体现在公式上，就是原问题的变量对应对偶问题的约束，目标系数对应约束边界，约束矩阵倒转过来。

另外，关于对偶，一个比较重要的特性是：原问题的最优值与对偶问题的最优值相等。

 从对偶角度看列生成算法

列生成算法主要用途在于求解变量多，但是大部分变量将会取值为0的线性规划问题。总体思路是先忽略大部分变量，构造一个只使用小部分变量的模型（其余变量相当于值为0），这样就能很快求出一个解。然后寻找模型外的变量，找到能够让目标值更优的变量，加入模型再次求解。重复这个过程直至找不到更好的变量。

这个过程的关键问题在于，怎么评估模型外的变量是否能让目标值更优。

我们从对偶的角度来研究这个问题。原问题的变量对应对偶问题的约束。所以原问题新增变量，相当于对偶问题新增约束。

原问题新增变量 -> 对偶问题新增约束

由于对偶问题是个最大化问题，所以对偶问题新增约束后，显然最优值不变或变差，也就是不变或变小。（约束越多限制越多，结果会越来越差，最好的结果仅仅是保持不变）

而原问题的最优值等于对偶问题的最优值。也就是说，如果对偶问题最优值不变，那么原问题最优值也不变；如果对偶问题最优值变小，那么原问题最优值也变小。而我们需要的正是让原问题的最优值变小。

所以问题变为如何尽量避免新增的约束没有改变最优值。设想一下，当加入新约束时，如果当前对偶的最优解没有违反新的约束，那么这个解仍然会是新增约束后的对偶问题的最优解，最优值将不变。

因此，我们要找的新增的约束，要和当前最优解冲突。

***************

新增变量后原问题最优解变小 -> 新增约束后对偶问题最优解变小 -> 新增约束前的最优解不在新增约束后的可行域 -> 新增约束前的最优解不满足新增的约束

*****************

一行对偶问题的约束的公式为：

假设最优解为w*，那么违反约束的条件为：

变换一下，变成：

左侧的式子，叫做的reduced cost，也叫做检验数。

通过分析，我们知道，只要加入reduced cost小于0的对偶约束（从而加入了原问题对应的变量）即可。

我们更倾向于找到reduced cost最小的一个或几个变量加入，也就是最好能找到最小化reduced cost的新约束：

这里就出现了一个新的最优化问题。这个问题叫做列生成的子问题（sub problem）。其中w*是已知的，未知量是c和a。c和a是和问题的应用场景有关的，需要根据实际场景来构造c和a的约束条件。所以子问题无法通用地求解，只能根据具体问题选择不同的方法求解。

当所有未加入模型的变量的reduced cost都大于等于0时，目标值无法再优化，说明我们已得到最优解。

 

3. Cutting Stock Problem

原纸卷每个长17m，顾客们分别需要25个3m长，20个5m长，18个7m长的纸卷。
问：如何切割使消耗的原纸卷数量最少？

令一个原纸卷的切割方案集合为：

P = {(a, b, c) | 3a + 5b + 7c <= 17}

其中，a是一个原纸卷切割出的3m纸卷数量，b是5m纸卷数量，c是7m纸卷数量。

我们用变量x(abc)表示使用切割方案(a, b, c)的原纸卷数量。

显然，一个变量与一个原纸卷切割方案一一对应。建模如下：

 

这里故意不使用传统的下标序号标记，意在突出我们不需要对变量编号，只需要知道变量在对应在什么集合上，如何通过集合中的元素生成变量就行了。

初始解很好找。比如说我们可以取25个原纸卷按照方案(1, 0, 0)切割，20个原纸卷按照方案(0, 1, 0)切割，18个原纸卷按照方案(0, 0, 1)切割。这当然会有很多浪费。但是初始解可行就可以了，浪费的部分会在下面的迭代中优化掉。

接下来要生成变量。变量与切割方案一一对应的。所以是要找出一个切割方案(a, b, c)，使得reduced cost最小。

 其中w1、w2和w3分别为约束R1、R2和R3的对偶值。（RC 为，其中c为1）

有两重含义：

• 通过求解RMP问题得到的影子价格（shadow price）。
• 通过求解RMP对偶问题得到的对偶变量(dual variable)。

约束条件除了a、b、c非负外，还需要满足切割后的纸卷长度综合小于或者等于原纸卷的长度。

这样子问题就构造好了。求解子问题得到新增变量。然后迭代直到最优。

4、应用实例

• P是所有可行的裁剪方案的集合，里面方案的总数为n(我们并不需要确切的知道这个值是多少，只需要知道它很大)。
• 表示第j种方案里类别i的个数。
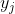• 表示第 j 种方案的选择个数。

于是，我们得到如下模型：

 使用LpsolveIDE，输入为：

                ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

首先，一个卷筒有三种切割方案：
方案1：切成5个3m
方案2：切成2个6m
方案3：切成2个7m

很容易得出，5个方案1、10个方案2、8个方案3，是能满足所有客户需求的。即得到MP的一个RMP（restricted master problem）如下：

                                                 

其中：

                                                        

这三列分别对应着5个方案1、10个方案2、8个方案3。还有一点需要注意的，对于每一列，都需要满足：

                                        

也就是每一卷纸只有16的长度，不能超出这个长度。这个叫列生成规则，不同问题有不同的规则约束。

正式迭代

iteration 1

RMP：

                                         

将该模型输入lpsolve，得到对偶变量如下：

                         

 得到       在要找一列加入RMP，是哪一列呢？现在还不知道，我们暂记为     。

非基变量检验数       

子问题：

                                

求解结果得        reducedcost为负数，因此将   加入RMP，开始第二轮迭代。

iteration 2

 RMP：

                                         

将该模型输入lpsolve，得到对偶变量如下：

        ​​​​​​​        

得到   ,现在要找一列加入RMP，我们暂记为。

 非基变量检验数       

子问题：

                                 

求解结果得  reducedcost为负数，因此将 加入RMP，开始第三轮迭代。

iteration 3

RMP：

                                 

 将该模型输入lpsolve，得到对偶变量如下：

                         

得到,现在要找一列加入RMP，我们暂记为。

 非基变量检验数    

subproblem：

        ​​​​​​​        ​​​​​​​        

求解结果得 ，reducedcost不为负数，因此不用将  加入RMP，列生成算法结束。

最终，我们求解最后一次迭代的RMP：

                                

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

得到RM的最优解    , 按理说y应该是整数才对。回到原问题

RM：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

我们并没有加上 这个约束，这是因为我们在用列生成的时候把这个模型给松弛为了线性模型，毕竟列生成是用于求解linear program的。如果要求解大规模整数规划问题，列生成是无法办到的，后面我们会介绍结合column generation的branch and price方法。

限制主问题和子问题的关系为：
​​​​​​​ 

 

5、列生成和分支定价

 

 

Reference：

【1】【学界】单纯形算法的原理和示例实现 

【2】  深入浅出列生成算法  

【3】 算法介绍之列生成算法   

【4】彻底了解column generation（列生成）算法的原理