梯度下降与线性回归+python代码
一、线性回归
1.1描述
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析,也称简单线性回归。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
1.2模型
一元线性回归: y = θ 0 + θ 1 x y=\theta_0+\theta_1x y=θ0+θ1x
多元线性回归: y = θ 0 + θ 1 x 1 + θ 2 x 2 + … + θ k x k y=\theta_0+\theta_1x_1+\theta_2x_2+\ldots+\theta_kx_k y=θ0+θ1x1+θ2x2+…+θkxk
二元曲线回归模型: y = θ 0 + θ 1 x + θ 2 x 2 y=\theta_0+\theta_1x+\theta_2x^2 y=θ0+θ1x+θ2x2
双曲线模型: y = a + b x y=a+\frac{b}{x} y=a+xb
二、简单线性回归
简单线性回归(Simple Linear Regression ),也就是一元线性回归,包含一个自变量x 和一个因变量y。
最小二乘法
模型(估值函数):
y ^ = b 0 + b 1 x \hat{y}=b_0+b_1x y^=b0+b1x
最小二乘法:
b 1 = ∑ ( x i − a ‾ ) ( y i − y ‾ ) ∑ ( x i − x ‾ ) 2 b_1=\frac{\sum{(x_i - \overline{a})}(y_i-\overline{y})} {\sum(x_i-\overline{x})^2} b1=∑(xi−x)2∑(xi−a)(yi−y)
b 0 = y ˉ − b 1 x ˉ b_0=\bar{y}-b_1\bar{x} b0=yˉ−b1xˉ
代码实例:
import numpy as np
import matplotlib.pyplot as plt
def Alg(x:list, y:list):
fenzi = 0.0
fenmu = 0.0
x_bar = np.mean(x) #x的均值
y_bar = np.mean(y) #y的均值
for i in range(len(x)):
fenzi += (x[i]-x_bar)*(y[i]-y_bar)
fenmu += (x[i]-x_bar)**2
b1 = fenzi/fenmu
b0 = y_bar - b1*x_bar
return b0,b1
def predict(x,b0,b1):
return b0+x*b1
if __name__ == "__main__":
y_predict = []
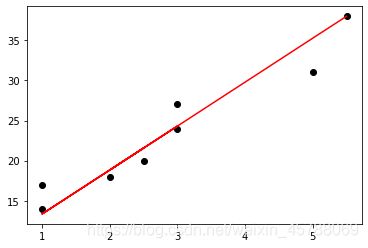
x = [1,3,2,2.5,1,3,5,5.5]
y = [14,24,18,20,17,27,31,38]
b0,b1 = Alg(x,y)
for i in range(len(x)):
y_predict.append(predict(x[i],b0,b1))
plt.plot(x, y, "ko")
plt.plot(x, y_predict, 'r-')
plt.show()
梯度下降法
设线性回归模型: h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1x hθ(x)=θ0+θ1x
构造损失函数:
J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1)=\frac{1}{2m}{\sum ^m_{i=1}}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ0,θ1)=2m1∑i=1m(hθ(x(i))−y(i))2
思路:通过迭代,不断更新 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1,当损失函数特别小后,就ok。
step1(求导):
∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial}{\partial{\theta_{0}}}J(\theta_0,\theta_1)=\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y{(i)}) ∂θ0∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))
∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) \frac{\partial}{\partial{\theta_{1}}}J(\theta_0,\theta_1)=\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y{(i)})\cdot x^{(i)} ∂θ1∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))⋅x(i)
step2(迭代):
θ 0 = θ 0 − α ⋅ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \theta_0=\theta_0-\alpha\cdot\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y{(i)}) θ0=θ0−α⋅m1i=1∑m(hθ(x(i))−y(i))
θ 1 = θ 1 − α ⋅ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) \theta_1=\theta_1-\alpha\cdot\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y{(i)})\cdot x^{(i)} θ1=θ1−α⋅m1i=1∑m(hθ(x(i))−y(i))⋅x(i)
step3:
代入损失函数,求损失函数的值,若得到的值小于 ϵ \epsilon ϵ(一般为0.01或0.001这样的小数),退出;否则,返回step1.
代码:
import matplotlib.pyplot as plt
import math
import random
def Alg(x:list,y:list,steps=10000,alpha=0.1,yuzhi=0.001):
#strps:梯度下降次数;alpha:步长;yuzhi:yuzhi
theta0 = random.uniform(0, 2) #参数初始值
theta1 = random.uniform(0, 2)
m = len(x)
for num in range(steps):
diss = 0.0 #误差
deriv0 = 0.0 #对theata0偏导
deriv1 = 0.0 #对theata1偏导
for i in range(m):
deriv0 += (theta0 + theta1*x[i]) - y[i]
deriv1 += ((theta0 + theta1*x[i]) - y[i])*x[i]
deriv0 /= m
deriv1 /= m
for i in range(m):
diss += pow(((theta0+theta1*x[i]) - y[i]),2)
diss /= (2*m)
if diss <= yuzhi:
#判断,是否达到退出要求
break
else:
theta0 = theta0 - alpha*(deriv0/m)
theta1 = theta1 - alpha*(deriv1/m)
return theta0,theta1
def predict(x,t0,t1):
return t0 + t1*x
if __name__ == "__main__":
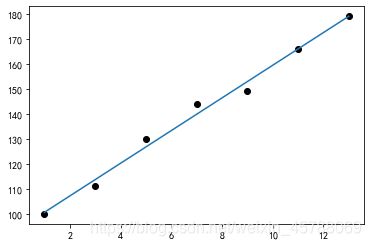
x = [1,3,5,7,9,11,13]
y = [100,111,130,144,149,166,179]
theta0,theta1 = Alg(x, y)
plt.plot(x,y,"ko")
y_predict = []
for i in range(len(x)):
y_predict.append(predict(x[i], theta0, theta1))
plt.plot(x,y_predict,'-')
plt.show()
三、多元线性回归
多元线性回归是最简单的机器学习模型,通过给定的训练数据集,拟合出一个线性模型,进而对新数据做出预测。
对应的模型:
h ( x ) = ∑ i = 0 n θ i x i = θ T x h(x)=\sum^n_{i=0}\theta_ix_i=\theta^Tx h(x)=i=0∑nθixi=θTx
n n n:特征数量。
损失函数:
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=21i=1∑m(hθ(x(i))−y(i))2
m m m:训练样本数量。
思路:
- 设计函数模型,有n个参数,目的就是要求得这n个参数;
- 确定其损失函数,目的是为了迭代;
- 获取数据;
- 初始参数值;可随机选定数值,选用random函数;
- 对参数求偏导;
- 更新参数;
- 不停迭代(5~6),直至损失参数<=阈值;
- 结果处理:可视化;
可参考一元线性回归的梯度下降
梯度下降算法
梯度下降算法是一种求局部最优解的方法,就是求得最优参数的算法。
1、核心公式(迭代):
θ j = θ j − α ∂ ∂ θ j J ( θ ) \theta_j=\theta_j-{\alpha}\frac{\partial}{\partial{\theta{j}}}J(\theta) θj=θj−α∂θj∂J(θ)
α \alpha α 表示学习速率,可以看作每次迭代步长
2、损失函数(loss):
J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=21i=1∑m(hθ(x(i))−y(i))2
3、步骤
- 设计一个函数模型,确定其损失函数;
- 设定 α \alpha α(步长), ε \varepsilon ε;
- 求各参数的偏导数:
f ′ ( x m 0 ) = ∂ y ∂ x m ( x m 0 ) , m = 1 , 2 , … , n f^\prime(x_{m_{0}})=\frac{\partial y}{\partial x_m}(x_{m_0}),m=1,2,\ldots,n f′(xm0)=∂xm∂y(xm0),m=1,2,…,n - 更新当前参数值,公式:
x m ′ = x m − ∂ y ∂ x m ( x m 0 ) , m = 1 , 2 , … , n x^\prime_m=x_m-\frac{\partial y}{\partial x_m}(x_{m_0}),m=1,2,\ldots,n xm′=xm−∂xm∂y(xm0),m=1,2,…,n - 如果参数变化量小于 ε \varepsilon ε,退出;否则返回第三步。
4、与最小二乘法比较
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。
梯度下降法是迭代求解,最小二乘法是计算解析解。
如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。
但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
5、梯度下降三类(BGD,SGD,MBGD)
批量梯度下降法(Batch Gradient Descent)
批量梯度下降法是每次都使用训练集中的所有样本更新参数。如果样本数据很多,那么迭代速度就会很慢。
优点:可得出全局最优解;
缺点:样本数据集大时,训练速度慢。
随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法是每次更新都从样本随机选择1组数据
有个缺点是,若其噪音多,那么每次迭代只会求得局部最优解;较BGD,取得可能不是全局最优解。
优点:训练速度快;
缺点:准确度下降。
小批量梯度下降法(Mini-batch Gradient Descent)
对于m个样本,采用n个样本来迭代,(1