数据结构(初始算法篇)-排序算法
数组排序算法
数组之常见的排序算法
排序:就是把一个无序的序列通过某种方式变成一个有序序列
冒泡排序
排序原理:
数组元素两两比较,交换位置,大元素往后放,那么通过一轮比较之后,最大数的元素,就会出现在最大索引处。
冒泡排序是一种比较简单的排序算法,它循环走过需要排序的元素,依次比较相邻的两个元素,如果顺序错误就交换,直至没有元素交换,完成排序。
若对n个人进行排序,我们需要n-1次比较,所以第k次比较需要进行n-k次比较。排序算法通过以数据对象的两两比较作为关键,所以可以得出,冒泡排序需要进行的
比较次数为:(n-1) + (n-2) + … + 1 = n*(n-1) / 2,因此冒泡排序的时间复杂度为O(n^2)。
算法简介:
1.比较相邻的元素,前一个比后一个大(或者前一个比后一个小)调换位置
2.每一对相邻的元素进行重复的工作,从开始对一直到结尾对,这步完成后,结尾为做大或最小的数.
3.针对除了最后一个元素重复进行上面的步骤。
4.重复1-3步骤直到完成排序
动画演示:
public class BubbleSort {
public static void main(String[] args) {
int[] arr = {24, 34, 1, 80, 23, 13, 57, 4};
System.out.println("排序前:"+Arrays.toString(arr));
int[] ints = PerfectSort();
System.out.println("排序后:"+Arrays.toString(ints));
}
//优化
public static int[] PerfectSort(){
int[] arr = {24, 34, 1, 80, 23, 13, 57, 4};
for (int j = 0; j < arr.length - 1 ; j++) {
for (int i = 0; i < arr.length - 1-j; i++) {
if (arr[i] > arr[i + 1]) {
int temp; //设定一个中间变量,存放数组元素的第一个元素
temp = arr[i];
arr[i] = arr[i + 1];
arr[i + 1] = temp;
}
}
}
return arr;
}
}
排序前:[24, 34, 1, 80, 23, 13, 57, 4]
排序后:[1, 4, 13, 23, 24, 34, 57, 80]
选择排序
排序原理:
从0索引开始,依次和后面的元素进行比较,小的元素往前放,经过一论比较之后,最小的元素出现在最小索引处。
选择排序是一种简单直观的排序算法,工作原理为:在未排序的序列中找出最小(大)元素与第一个位置的元素交换位置
注意选择排序与冒泡排序的区别:冒泡排序通过依次交换相邻两个顺序不合法的元素位置,从而将当前最小(大)元素放到合适的位置;而选择排序每遍历一次都记住了当前最小(大)元素的位置,最后仅需一次交换操作即可将其放到合适的位置。
然后在剩下的元素中再找最小(大)元素与第二个元素的位置交换,依此类推,直到所有元素排序排序完成。根据上述描述,一共进行n-1趟比较后,就能完成整个排队过程。我们可以知道,第k趟比较需要进行的数组元素的两两比较的次数为n-k次,所以共需要的比较次数为n*(n-1) / 2,因此选择排序算法的时间复杂度与冒泡排序一样,也为O(n^2)。
算法简介:
1.初始状态:序列为无序状态。
2.第1次排序:从n个元素中找出最小(大)元素与第1个记录交换
3.第2次排序:从n-1个元素中找出最小(大)元素与第2个记录交换
4.第i次排序:从n-i+1个元素中找出最小(大)元素与第i个记录交换
5.以此类推直到排序完成
public class SelectSort {
public static void main(String[] args) {
int[] arr = {24, 69, 60, 45, 13};
System.out.println("排序前:" + Arrays.toString(arr));
PerfectSelectSort(arr);
System.out.println("排序后:" + Arrays.toString(arr));
}
public static void PerfectSelectSort(int[] arr) {
for (int i = 0; i < arr.length-1; i++) {
for (int j = 1+i; j < arr.length; j++) {
if (arr[i] > arr[j]) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
}
}
}
排序前:[24, 69, 60, 45, 13]
排序后:[13, 24, 45, 60, 69]
插入排序
排序原理
直接插入排序,是一种最简单的排序方法,他基本的操作是将一个记录插入到长度为m的有序表中,使之仍保持有序。
例如:
49,38,69,57,79,13,47 原始数据
[49],38,65,97,76,13,27 从1索引开始插入
[38,49],65,97,76,13,27
[38,49,65],97,76,13,27
[38,49,65,97],76,13,27
[38,49,65,76,97],13,27
[13,27,38,49,65,76,97],27
[13,27,38,49,65,76,97]
public class DirectInsertionSort {
public static void main(String[] args) {
//从1索引处,将一个元素插入到该索引处,使之成为一个有序的序列
int[] arr = {49, 38, 65, 97, 76, 13, 27};
//外层循环,定义轮次
// for (int i = 1; i < arr.length; i++) {
// //里层循环,进行插入比较
// int j = 1;
// while (j > 0 && arr[j] < arr[j - 1]) {
// //交换
// int t = arr[j];
// arr[j] = arr[j - 1];
// arr[j - 1] = t;
// j--;
// }
// }
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0; j--) {
if (arr[j] < arr[j - 1]) {
swapValue(arr,j,j-1);
}
}
}
System.out.println(Arrays.toString(arr));
}
public static void swapValue(int[] arr, int i, int j) {
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
}
[13, 27, 38, 49, 65, 76, 97]
希尔排序
排序思想
希尔排序:又称为减小增量排序,是对插入排序的优化,可以理解为增量为1的直接插入排序
基本思路:先将原表按照增量ht分组,每个子文件按照直接插入法排序。同样,用下一个增量ht/2将文件再分为子文件,在直接插入排序。知道ht = 1整个文件排好序。
关键:选择合适的增量
希尔排序算法:可以通过三重循环实现
public class HillSort {
public static void main(String[] args) {
int[] arr = {45, 23, 34, 12, 3, 78, 32};
/*
第一轮排序
* 45,23,34,12,3,78,32
* [45,3] 换
* 3,23,34,12,45,78,32
* [23,78] 不换
* 3,23,32,12,45,78,34
* [32,34] 换
* [3, 23, 32, 12, 45, 78, 34]
* */
perfectHillSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void perfectHillSort(int[] arr){
for (int h = (arr.length/2); h >0 ; h/=2) { // 计算间隔的元素数:使用数组的长度一半
for (int i = h; i < arr.length; i++) {
for (int j = i; j > h-1; j-=h) {
if (arr[j] < arr[j - h]) {
swapValue(arr,j,j-h);
}
}
}
}
}
}
克努特计算间隔数
public static void perfectHillSort(int[] arr){
// 计算间隔的元素数:使用克努特序列
int jiange = 1;
while (jiange <= arr.length / 3) {
jiange = jiange*3+1;
}
for (int h = jiange; h >0 ; h=(h-1)/3) { // 计算间隔的元素数:使用数组的长度一半
for (int i = h; i < arr.length; i++) {
for (int j = i; j > h-1; j-=h) {
if (arr[j] < arr[j - h]) {
swapValue(arr,j,j-h);
}
}
}
}
}
快速排序
快速排序的思想
分治法:比大小,再分区
1.从数组中取出一个数,作为基准数。
2.分区:将比这个数大或等于的数全放到他的右边,小于他的数
全放到他的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。
代码展示
public class QuickSortUtils {
public static void quickSort(int[] arr, int start, int end) {
//找出分左右两区的索引位置,然后对左右两边进行递归调用
if (start < end) {
int index = getindex(arr, start, end);
quickSort(arr, start, index - 1); // 左边分区
quickSort(arr, index + 1, start); // 右边分区
}
}
public static int getindex(int[] arr, int start, int end) {
int i = start;
int j = end;
int x = arr[i];
while (i < j) {
//从后往前找
while (i < j && arr[j] >= x) {
j--;
}
if (i < j) {
arr[i] = arr[j];
i++;
}
//从前往后找
while (i < j && arr[i] < x) {
i++;
}
if (i < j) {
arr[j] = arr[i];
j--;
}
}
arr[i] = x; //把基准数填到最后一个坑中
return i;
}
}
public class QuickSort {
public static void main(String[] args) {
int[] arr = {10,3,5,6,0,100,45,24,8};
QuickSortUtils.quickSort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
}
[0, 3, 5, 6, 8, 10, 45, 24, 100]
归并排序
排序思想
归并排序(Merge Sort)就是利用归并的思想实现排序的方
法。
它的原理是假设初始序列有N个记录,则可以看成是N个
有序的子序列,每个子序列的长度为1,然后两两归并,
得到N/2个长度为2或1的有序子序列,再两两归并…
如此重复,直至得到一个长度为N的有序序列为止,这种
排序方法称为2路归并排序。
代码演示 递归算法
public class MergeSort {
public static void main(String[] args) {
//原始数组
int[] arr = {2,3,4,1};
mergeSort(arr);
//输出
System.out.println(Arrays.toString(arr));
}
private static void mergeSort(int[] array) {
sort(array,0,array.length-1);
}
private static void sort(int[] array, int start, int end) {
if(start < end) {
int mid = (start+end)/2;
sort(array,start,mid);
sort(array,mid+1,end);
merge(array,start,mid,end);
}
}
private static void merge(int[] array, int start, int mid, int end) {
//定义两个指针
int i = start;
int j = mid+1;
//定义一个临时数组和数组的指针
int[] temp = new int[end-start+1];
int index = 0;
while (i <= mid && j <= end) {
if(array[i] < array[j]) {
temp[index++] = array[i++];
} else {
temp[index++] = array[j++];
}
}
while (i <= mid) {
temp[index++] = array[i++];
}
while (j <= end) {
temp[index++] = array[j++];
}
for (int k = 0; k < index; k++) {
array[start++] = temp[k];
}
}
}
基数排序
排序原理
基数排序时根据基数不同 将不同的数分配到不同的桶中,(最低位优先)基数排序先对根据数列的个位数 将其放入0-9的二维数组中 然后以此对十位数 百位数等进行相同操作 最后得到一个有序数列,当然最高位优先其思想也是一样
public class BaseSort {
public static void main(String[] args) {
int[] arr = {6, 10, 25, 80, 612, 8, 12, 15, 9, 6, 7};
radixSort(arr);
}
public static void radixSort(int[] arr) {
/* 创建一个10*arr.length的二维数组 */
int[][] duck = new int[10][arr.length];
/* 先获取最大值 */
int max = arr[0];
for (int i = 0; i < arr.length; i++) {
if (arr[i] > max) {
max = (int) (arr[i] + 1);
}
}
for (int i = 1; max > 0; i *= 10) {
/* 记录每个桶的下标 */
int[] count = new int[10];
for (int j = 0; j < arr.length; j++) {
int t = (arr[j] / i) % 10;
duck[t][count[t]++] = arr[j];
}
/* 将桶中的数放回原数组 等待下一位数的排序 */
for (int j = 0, c = 0; j < 10; j++) {
for (int k = 0; k < count[j]; k++) {
arr[c++] = duck[j][k];
}
}
max /= i;
}
System.out.println(Arrays.toString(arr));
}
}
[6, 6, 7, 8, 9, 10, 12, 15, 25, 80, 612]
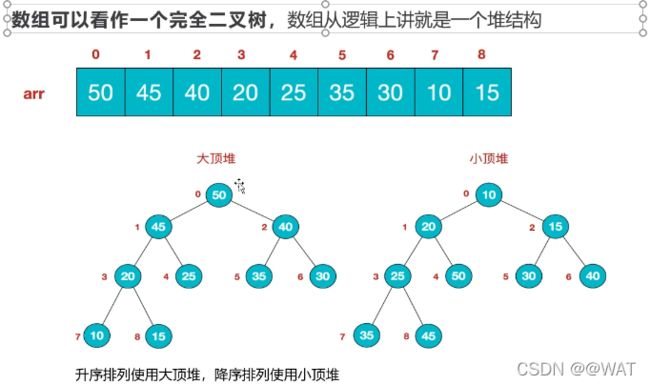
堆排序
排序原理
堆排序是利用堆这种数据结构而设计的一种排序算法, 堆排
序是一种选择排序
堆排序的基本思想是:
-
将待排序序列构造成一个大顶堆, 此时,整个序列的最大值就是堆顶的根节点。
-
将其与末尾元素进行交换,此时末尾就为最大值。
-
然后将剩余n-1个元素重新构造成一一个堆 ,这样会得到n个元素的次小值。
-
如此反复执行,便能得到一个有序序列了.
动图展示
代码展示
public class HeapSort {
public static void main(String[] args) {
//定义一个数组
int[] arr = {1, 0, 6, 7, 2, 3, 4};
//调成大顶堆
toMaxheap(arr, arr.length, 1);
//我们定义要调整的位置
int startIndex = (arr.length - 1) / 2;
//循环开始调整
for (int i = startIndex; i >= 0; i--) {
toMaxheap(arr, arr.length, i);
}
//经过以上操作之后,已经把数组变成了一个大顶堆,把元素和最后一个元素进行调整
for (int i = arr.length - 1; i > 0; i--) {
//调换
int t = arr[0];
arr[0] = arr[i];
arr[i] = t;
//换完之后,再把剩余元素i调成大顶堆
toMaxheap(arr,i,0);
}
System.out.println(Arrays.toString(arr));
}
/**
* @param arr 要排序的数组
* @param size 调整的元素个数
* @param index 从哪里开始调
*/
private static void toMaxheap(int[] arr, int size, int index) {
//获取钟左右子节点的索引
int leftIndexNode = index * 2 + 1;
int rightIndexNode = index * 2 + 2;
//查找最大节点对应的索引
int maxIndex = index;
if (leftIndexNode < size && arr[leftIndexNode] > arr[maxIndex]) {
maxIndex = leftIndexNode;
}
if (rightIndexNode < size && arr[rightIndexNode] > arr[maxIndex]) {
maxIndex = rightIndexNode;
}
//调换位置
if (maxIndex != index) {
int t = arr[maxIndex];
arr[maxIndex] = arr[index];
arr[index] = t;
//调换完之后,可能会影响到下面的子树,我们要再次调换
toMaxheap(arr, size, maxIndex);
}
}
}
[0, 1, 2, 3, 4, 6, 7]
参考引用:必学十大经典排序算法,看这篇就够了(附完整代码动图优质文章)
tIndexNode < size && arr[rightIndexNode] > arr[maxIndex]) {
maxIndex = rightIndexNode;
}
//调换位置
if (maxIndex != index) {
int t = arr[maxIndex];
arr[maxIndex] = arr[index];
arr[index] = t;
//调换完之后,可能会影响到下面的子树,我们要再次调换
toMaxheap(arr, size, maxIndex);
}
}
}
```text
[0, 1, 2, 3, 4, 6, 7]
参考引用:必学十大经典排序算法,看这篇就够了(附完整代码动图优质文章)