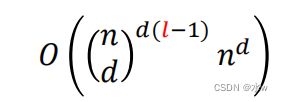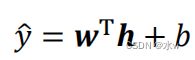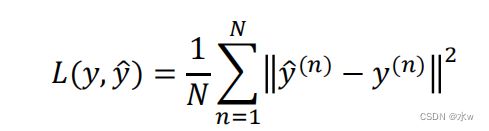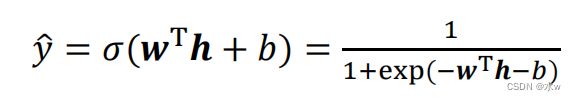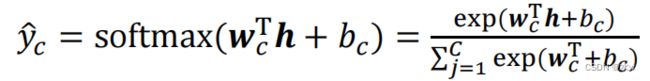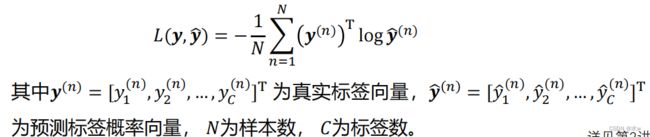深度学习之 7 深度前馈网络
本文是接着上一篇深度学习之 6 线性回归实现2_水w的博客-CSDN博客
目录
深度前馈网络
人工神经网络
1、人脑神经网络
2、一个解决异或问题的简单网络
3、神经网络结构
前馈神经网络
1、前馈神经网络的结构和表示：
2、隐藏单元——激活函数：
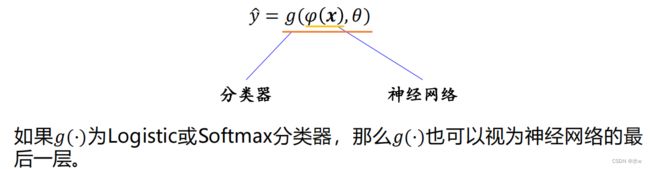
3、输出单元
4、前馈神经网络参数学习
反向传播算法
1、微分链式法则
2、反向传播算法
◼ 代码过程：
深度前馈网络
人工神经网络
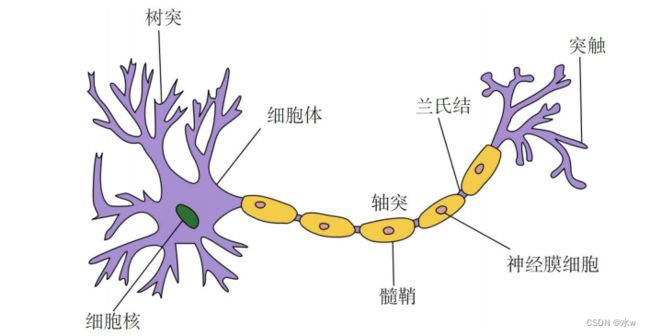
1、人脑神经网络
◼ 人类大脑由 神经元 、 神经胶质细胞 、 神经干细 胞 和 血管 组成◼ 神经元(neuron) 也叫神经细胞(nerve cell)，是人脑神经系统中最基本的单元◼ 人脑神经系统包含近 860亿 个神经元◼ 每个神经元有上千个 突触 与其他神经元相连◼ 人脑神经元连接成巨大的复杂网络，总长度可达 数千公里
（1）神经元结构：
◼ 细胞体 ：通过生物化学反应，引起细胞膜内外 电位差 发生改变，形成 兴奋 或 抑制 状态
◼ 细胞突起 ：由细胞体延伸出来，又可分为树突和轴突：
✓ 树突 ：可 接收 刺激并将兴奋传入细胞体，每个神经元可以有一个或多个树突
✓ 轴突 ：可把自身兴奋状态从细胞体 传给另一个神经元 ，每个神经元 只有一个 轴突
（2）神经元之间的信息传递：
◼ 每个神经元与其他神经元相连，当它“ 兴奋 ”时，就会向相连的神经元 发送化学物质 ，从而改变这些神经元内的 电位 ；
◼ 如果神经元的电位超过一定“ 阈值 ”，它就会被 激活 ，即“ 兴奋 ”起来，然后向其他神经元 发送化学物质 。
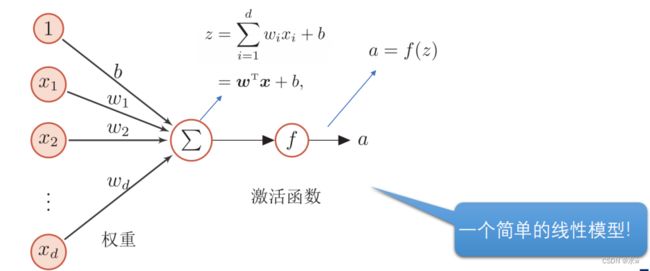
（3）人工神经元：
◼ M-P神经元模型（McCulloch and Pitts，1943） ：神经元接收到来自其他 个神经元 传递过来的 输入信号 ，这些输入信号通过 带权重的连接 进行传递，神经元接收到的 总输入值 将与神经元的 偏 置（bias） 进行比较，然后通过 “激活函数 ” 处理产生神经元的 输出 。
（4）人工神经网络：
◼ 把许多人工神经元按一定的 层次结构连接 起来，就形成 人工神经网络 。
◼ 人工神经网络的三大要素：
✓ 节点 —— 采用什么激活函数？
✓ 连边 —— 权重（参数）是多少？
✓ 连接方式 —— 如何设计层次结构？
2、一个解决异或问题的简单网络
（1）感知器求解异、或、非及异或问题：
输入为[1; 2]的单层单个神经元（输入层不计入层数），采用阶跃激活函数。
（2）双层感知器 —— 一个简单的神经网络
◼ 输入仍为[1; 2]，让网络包含两层：
✓ 隐藏层 包含两个神经元： = (1) (; , )
✓ 输出层 包含一个神经元： = (2) (; , )
✓ 隐藏层采用线性整流激活函数(ReLU)，则整个模型为：
(; , , , ) = 2 ( 1 ())
= Τ max 0, T + +
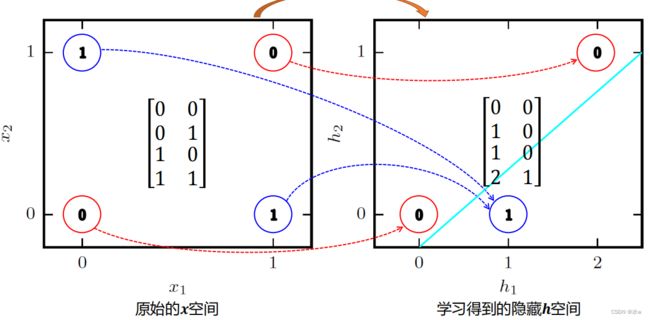
◼ 给出异或问题的一个解：
◼ 解释：非线性空间变换
3、神经网络结构
（1）万能近似定理：
（2）万能近似定理应用到神经网络：
◼ 根据万能近似定理，对于具有 线性输出层 和 至少一个 使用“挤压”性质的激活函数的 隐藏层 组成的神经网络，只要其隐藏层神经元的数量足够多，它就可以以任意精度来近似任何一个定义在实数空间中的有界闭集函数。◼ 神经网络 可以作为一个 “万能”函数 来使用，可以用来进行复杂的特征转换，或逼近一个复杂的条件分布。
（3）为什么要深度：
◼ 单隐层网络 可以近似任何函数，但其 规模可能巨大✓ 在最坏的情况下，需要 指数级的隐藏单元 才能近似某个函数[Barron, 1993]◼ 随着 深度的增加 ，网络的 表示能力呈指数增加✓ 具有 个输入、深度为 、每个隐藏层具有个单元的深度整流网络可以描述 的线性区域的数量为，意味着，描述能力为深度的 指数级
◼ 更深层的网络具有更好的泛化能力：模型的性能随着随着深度的增加而不断提升
◼ 参数数量的增加 未必 一定会带来模型效果的提升：更深的模型往往表现更好，并不仅仅是因为模型更大。 想要学得的函数应该由许多更简单的函数复合在一起而得到。
（4）常见的神经网络结构：
◼ 前馈网络
✓ 各个神经元按照接收信息的先后分成不同的组，每一组可看作一个神经层
✓ 每一层中的神经元接收来自前一层神经元的输出，并输出给下一层神经元
✓ 整个网络中信息 朝一个方向传播 ，没有反向的信息传播，可以用一个有向无环图表示
✓ 前馈网络包括 全连接前馈神经网络 和 卷积神经网络
◼ 记忆网络（反馈网络）
✓ 神经元不但可以接收其他神经元的信息，也可以接收自己的 历史信息
✓ 神经元具有记忆功能，在 不同的时刻具有不同的状态
✓ 信息传播可以是 单向或者双向 传递，可用一个有向循环图或无向图来表示
✓ 记忆网络包括 循环神经网络 、 Hopfield网络 、 玻尔兹曼机 、 受限玻尔兹曼机 等
◼ 图网络
✓ 图网络是定义在 图结构数据 上的神经网络；
✓ 图中的每个节点都是由 一个 或者 一组 神经元构成；
✓ 节点之间的连接可以是 有向 的，也可以是 无向 的；
✓ 每个节点可以接收来自 相邻节点 或者 自身 的信息；
✓ 图网络是前馈网络和记忆网络的融合方法，包含许多不同的实现方式，如 图卷积网络 、 图注意力网络 、 消息传递网络 等。
其他结构设计方面的考虑：除了深度和宽度之外，神经网络的结构还具有其他方面的多样性。
- 改变层与层之间的连接方式
✓ 前一层的每个单元仅与后一层的一个小单元子集相连✓ 可以极大地减少参数的数量✓ 具体的连接方式高度依赖于具体的问题
- 增加跳跃连接
✓ 从第 层与第 + 2 层甚至更高层之间建立连接✓ 使得梯度更容易从输出层流向更接近输入的层，利于模型优化
前馈神经网络
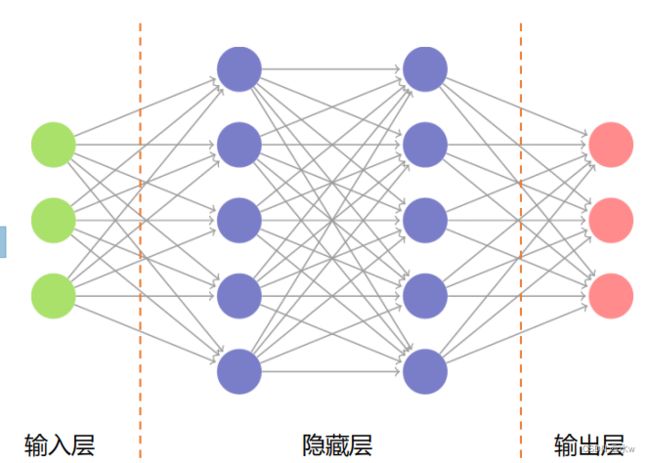
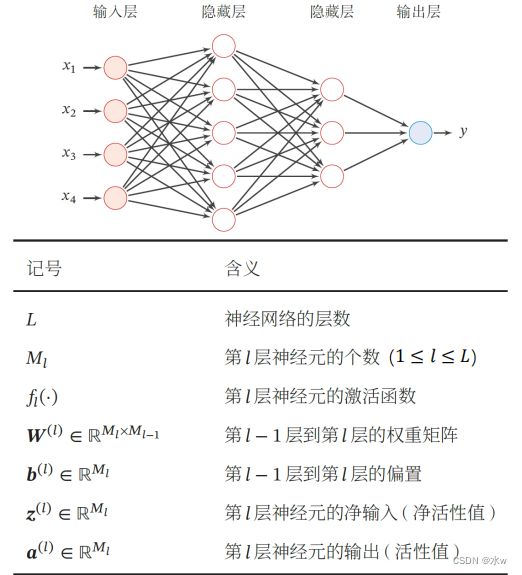
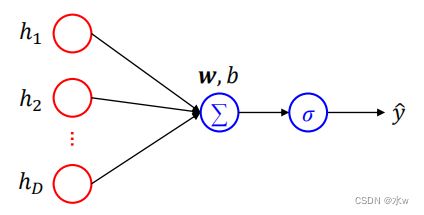
1、前馈神经网络的结构和表示：
◼ 前馈神经网络(Feedforward Neural Network, FNN)是最早发明的简单人工神经网络前馈神经网络也经常被称为 多层感知器 (Multi-Layer Perceptron, MLP)，但这个叫法并不十分合理（ 激活函数通常并不是感知器所采用的不连续阶跃函数 ）；◼ 第0层为输入层，最后一层为输出层，其他中间层称为隐藏层；◼ 信号从输入层向输出层单向传播，整个网络中无反馈，可用一个 有向无环图 表示；
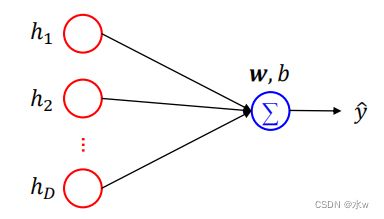
◼ 前馈神经网络的符号表示 ：
◼ 前馈神经网络的信息传递：
2、隐藏单元——激活函数：
◼ 隐藏单元的设计是一个非常活跃的研究领域，但是目前还没有很明确的指导原则◼ 激活函数的性质要求：✓ 连续并可导 （允许少数点上不可导）的 非线性 函数。可导的激活函数可以直接利用数值优化的方法来学习网络参数。✓ 激活函数及其导函数要尽可能的简单 ，有利于提高网络计算效率。✓ 激活函数的 导函数的值域要在一个合适的区间内 ，不能太大也不能太小，否则会影响训练的效率和稳定性。
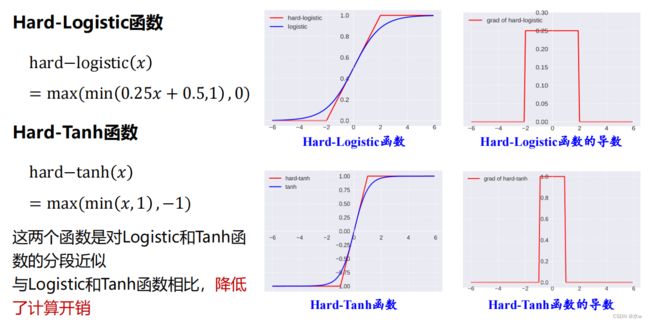
（1）Sigmoid型函数：
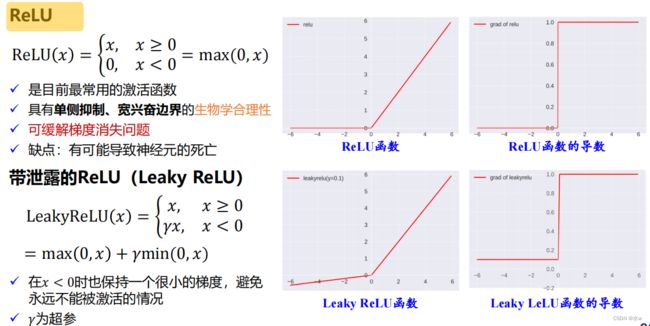
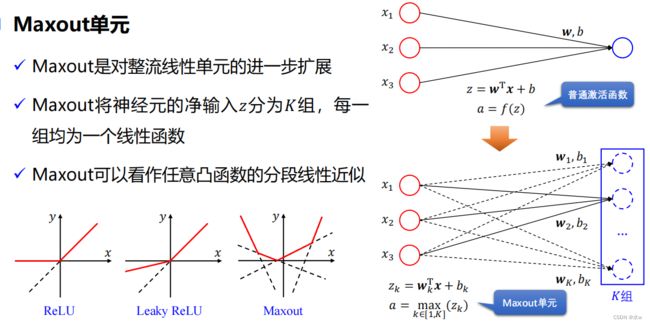
◼整流线性单元(ReLU)函数及其扩展 ：
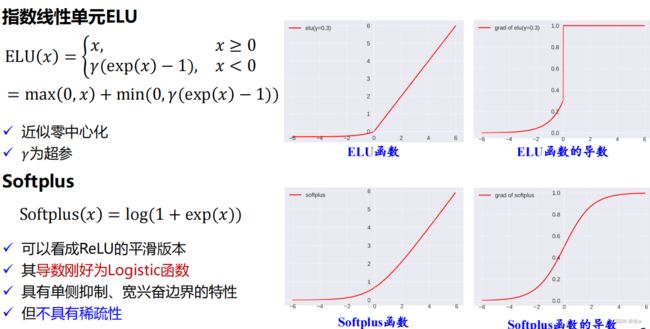
◼其他激活函数 ：
3、输出单元
◼ 线性输出单元 
✓ 线性输出单元经常用于产生 条件高斯分布的均值✓ 适合 连续值预测（回归） 问题✓ 基于高斯分布，最大化似然（最小化负对数似然）等价于最小化均方误差， 因此线性输出单元可采用均方误差损失函数：
其中() 为真实值， 为预测值， 为样本数。
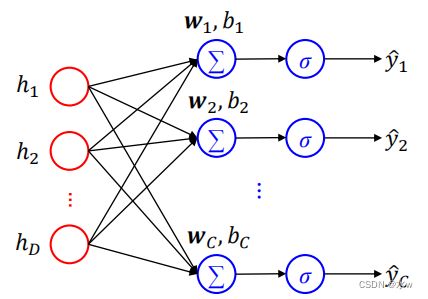
◼ Sigmoid单元： 
✓ Sigmoid输出单元常用于输出Bernoulli分布✓ 适合二分类问题✓ Sigmoid输出单元可采用 交叉熵损失函数 ：
◼ Softmax单元：
✓ Softmax输出单元常用于输出Multinoulli分布✓ 适合多分类问题✓ Softmax输出单元可采用 交叉熵损失函数 ：
4、前馈神经网络参数学习
◼ 学习准则✓ 假设神经网络采用交叉熵损失函数，对于一个样本 (, ) ，其 损失函数 为
◼ 梯度下降✓ 基于学习准则和训练样本，网络参数可以通过梯度下降法进行学习，✓ 通过链式法则可以逐一对每个参数求偏导，但是效率低下；✓ 在神经网络的训练中经常使用 反向传播算法 来高效地计算梯度；
反向传播算法
1、微分链式法则
2、反向传播算法
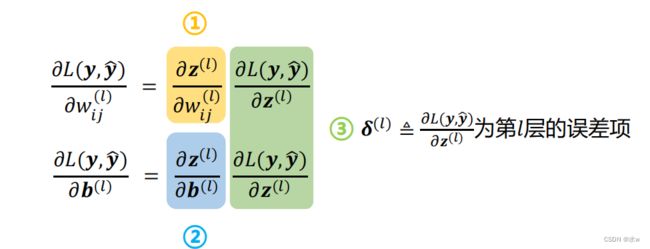
给定一个样本(, )，假设神经网络输出为y^，损失函数为(, ^)，采用梯度下降法需要计算 损失函数关于每个参数的偏导数。
◼ 如何计算前馈神经网络中参数的偏导数 —— 反向传播(Back Propagation，BP)算法
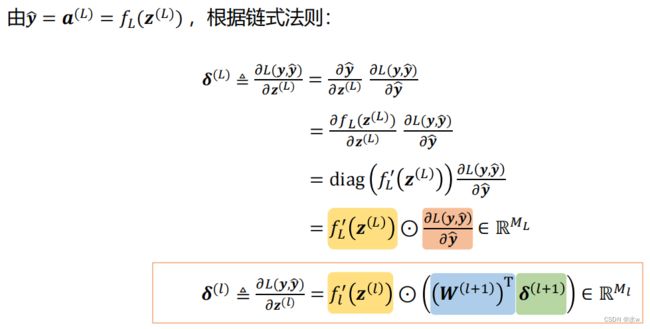
考虑求第层中参数()和()的偏导数，由于() = ()(−1) + ()，根据链式法则：
◼ 对于最后一层（输出层）的误差项
◼
◼ 代码过程：
