股指期货高频数据机器学习预测（Python）

代码详见：股指期货高频数据机器学习预测
主要学习本文对特征的提取和数据预处理操作

问题描述

通过对交易委托账本（订单簿）中数据的学习，给定特定一只股票10个时间点股票的订单簿信息，预测下20个时间点中间价的均值。

评价标准为均方根误差。

交易时间为工作日9:30-11:30,13:00-15:00，快照频率3秒。

股价的形成分为集合竞价和连续竞价

• 集合竞价：9:15-9:25，开盘集合竞价，确定开盘价
• 连续竞价：9:30之后，根据买卖双方的委托形成的价格

竞价原则：价格优先，时间优先。

交易委托账本具体信息：

• Date - 日期
• Time - 时间
• MidPrice - 中间价（买入价与卖出价的平均值）
• LastPirce - 最新成交价
• Volume - 当日累计成交数量
• BidPrice1 - 申买最高价
• BidVolume1 - 申买最高价对应的量
• AskPrice1 - 申卖最高价
• AskVolume1 - 申卖最高价对应的量

问题分析

在这个问题中，我们利用10个时间点股票的订单簿信息，预测特定一只股票下20个时间点中间价的均值，来判断其在一分钟内的价格变化特征，以便于高频交易。高频交易的意义在于，对于人类来说，很难在一分钟之内判断出股价变化情况，并完成交易。因此，只能利用计算机进行自动化交易。
对于无信息无模型预测，即利用订单簿中最后一个价格“预测”，得到的均方根误差为0.00155。试图通过分析数据、建立模型，做出高于此误差的预测。

数据分析

数据集

训练集（raw training data，train_data.csv）：430039条订单簿信息
测试集（test data, test_data.csv）：1000条（100组）订单簿信息
为了避免概念的混淆，下文中如果特别说明，“测试集”均指public board所依赖的数据。此外，这里的“训练集”下文中包含经过数据清理和预处理的训练集（training data）和验证集（test data）。

数据清洗

为了将训练集转换为测试集的格式，即通过10个间隔3秒的订单簿记录，来预测后20个间隔3秒的订单簿记录中中间价的均值，必须对数据清洗。
将训练集集中连续的nGiven+(nPredict平方)条数据作为一组数据。
检查每一组数据，去掉含有时间差不为3秒的连续两条数据的组。这样可以跳过跨天的以及不规整的数据。

数据预处理

归一化

给定的数据特征（日期、时间、价格、成交量等）的量纲不同，并且数据绝对值差的较大。如测试集第一条数据：

MidPrice和Volume差6个数量级。
首先，数据归一化后，最优解的寻优过程明显会变得平缓，更容易正确地收敛到最优解。
其次，在支持向量机(SVM)等不具有伸缩不变性的模型中，大数量级的数据会掩盖小数量级的数据。这是因为随机进行初始化后，各个数据拥有同样的或近似的缩放比例，相加之后小数量级的数据便被大数量级的数据“吃掉了”。
此外，对于具有伸缩不变性的模型，如逻辑回归，进行归一化也有助于模型更快地收敛。
综上所述，对模型进行归一化是十分有必要的。

Prices

训练集MidPrice分布：

测试集MidPrice分布：

从上面两张图片中可以看出，训练集和测试集中最重要的特征以及待遇测量——中间价只有约三分之一重合。这意味着如果按照数值直接进行归一化，可能会有较差的结果。

我采取的第一种方式是预测差值：即每组数据待预测量为下20条数组中MidPrice的均值与最后一个MidPrice的差值，并将各个价格减去最后一个MidPriced的值，这样可以使训练集和验证集分布更为接近，但是这样造成的问题是，在量纲存在的情况下，最后一个MidPriced的值仍是有价值的，将它直接消去不合适。

第二种方式是完全消除量纲，将预测任务变为变化率的预测。即将所有与Price相关的变量都减去并除以最后一条数组的中间价。 这样就可以将量纲完全消除。

for axis in [-1, 0, 3, 4]: # MidPrice, LastPrice, BidPrice1, AskPrice1
    x_cur[:, axis] -= last_mp
    x_cur[:, axis] /= last_mp
...
y.append((np.mean(mid_price[k+nGiven: k+nGiven+nPredict]) - mid_price[k+nGiven-1]) / mid_price[k+nGiven-1])

Volume

Volume是指当日累计成交数量。在每组数据中，Volume的大小差别很大，这主要是因为每组数据开始的时间不同。开始，我试图保留时间信息和Volume，来更好地利用Volume信息。事实上，虽然一天中的Volume是相关的，但是几乎不可能通过时间信息来估计Volume，何况高频交易簿的精度很高。因此，通过加入时间信息避免对Volume的归一化是不可行的。

第二个尝试是利用类似于对Prices的处理，将每组数据中的Volume减去该组数据中第一条数据的Volume。但这样效果并不好，这是因为Volume在一组中是递增的，将它们进行如上处理后仍是递增的，利用普通的归一化手段无法将它们映射在同一尺度上。

第三种尝试是利用变化量。将每一组Volume数据减去上一条信息的Volume，将这个特征转化为：3秒内累计成交数量。至此，每组/条数据的Volume便为同一分布了。 此外，对于第一条数据，没有办法得知它与上一条数据（没有给出）的差值，只能用均值填充。具体方法是利用迄“今”（这条数据）为止得到的Volume插值的均值。

for i in range(nGiven-1, 0, -1):
    x_cur[i, 1] -= x_cur[i-1, 1]
    volume_sum += x_cur[i,1]
    volume_len += 1
x_cur[0, 1] = volume_sum / volume_len 

时间信息

由于时间是递增的，可以通过将它们映射在每一天（即，删除日期，保留时间），然后进行预测。但是由于数据只有约120天，将它们映射在每一个时间点会导致这部分数据过于稀疏。因此，在保证每组数据中，每连续两条数据的时间差值为3秒的情况下，可以直接将时间信息删除。

此外，我发现在多种模型的实验中，是否将时间信息加入并不会有太大的改变。

对于预测值的处理

在前文中提到过，将预测数值任务改变为预测变化率的任务。这样做除了为了消除量纲，更主要的原因是加快收敛。若果不进行这样的处理，对于CNN/DNN/RNN等基于神经网络的模型，需要大约20epoch才能收敛到baseline RMSE=0.00155，但是如果采取变化率预测，只需要一个epoch就可以收敛到RMSE=0.00149.4

因此，如果不进行这样的处理，将会极度增加训练的时间，对调参和模型分析造成很大困难。

噪声

加入噪声。对于某些数据而言——尤其是Price相关的数据，由于有很多组相同或相似的数组以及线性映射的不变性，导致处理后结果是离散的。因此，我在每个值中加入±1%的噪声，以提高模型的泛化能力。

x_cur *= (1 + 0.001 * (np.random.rand(nGiven, nFeature) - 0.5) * 2)  # 加入噪声

降低噪声。在固定模型的情况下，我发现改变任务为预测下15条数据的中间价均值，亦或是下10条数据的中间价均值，得到的leaderboard成绩要优于预测下20条的数据的中间价均值。我想这是因为通过跨度为30秒的10条数据可能无法预测到更远的时间点，如跨度为60秒的20条数据中的后几条数据。在没有更多信息的情况下，很可能之后的数值对于预测来说是噪声。在实验中也证明了这一点，后文将会详细说明。在下文中将这个nPredict“超参数”视为MN（Magic Number）。

模型探索

基于LSTM的RNN模型

这个模型是我所实现最优的模型，采取这个模型的主要原因是基于LSTM的RNN模型具有很好的处理时间序列的能力。

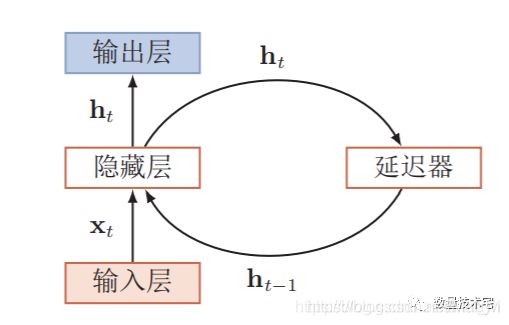
递归神经网络(RNN)

循环神经网络（Recurrent Neural Network，RNN）是一类具有短期记忆能力的神经网络。在循环神经网络中，神经元不但可以接受其它神经元的信息，也可以接受自身的信息，形成具有环路的网络结构。和前馈神经网络相比，循环神经网络更加符合生物神经网络的结构。循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等任务上。循环神经网络的参数学习可以通过随时间反向传播算法 [Werbos, 1990] 来学习。随时间反向传播算法即按照时间的逆序将错误信息一步步地往前传递。当输入序列比较长时，会存在梯度爆炸和消失问题[Bengio et al., 1994, Hochreiter and Schmidhuber, 1997, Hochreiteret al., 2001]，也称为长期依赖问题。为了解决这个问题，人们对循环神经网络进行了很多的改进，其中最有效的改进方式引入门控机制。

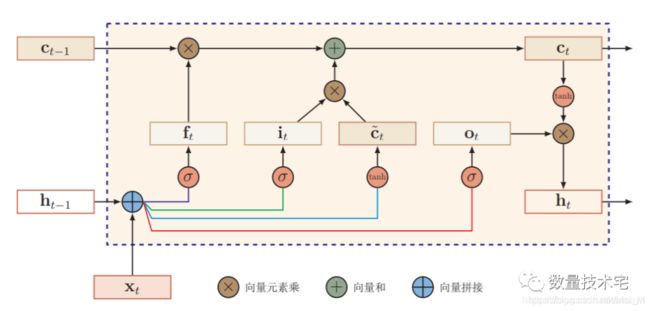
长短期记忆（LSTM）网络

长短期记忆（long short-term memory，LSTM）网络 [Gers et al., 2000, Hochreiter and Schmidhuber, 1997]是循环神经网络的一个变体，可以有效地解 决简单循环神经网络的梯度爆炸或消失问题。在公式(6.48)的基础上，LSTM网络主要改进在以下两个方面：新的内部状态 LSTM网络引入一个新的内部状态（internal state）ct专门进行线性的循环信息传递，同时（非线性）输出信息给隐藏层的外部状态ht。
在每个时刻t，LSTM网络的内部状态ct记录了到当前时刻为止的历史信息。
循环神经网络中的隐状态h存储了历史信息，可以看作是一种记忆（memory）。在简单循环网络中，隐状态每个时刻都会被重写，因此可以看作是一种短期记忆（short-term memory）。在神经网络中，长期记忆（long-term memory）可以看作是网络参数，隐含了从训练数据中学到的经验，并更新周期要远远慢于短期记忆。而在LSTM网络中，记忆单元c可以在某个时刻捕捉到某个关键信息，并有能力将此关键信息保存一定的时间间隔。记忆单元c中保存信息的生命周期要长于短期记忆h，但又远远短于长期记忆，因此称为长的短期记忆（long short-term memory）

模型实现

利用Keras框架，实现基于LSTM的RNN模型。具体结构为两层LSTM网络和两层Dense层网络。试图利用LSTM网络提取时间序列中的特征信息，并利用Dense层将提取出的特征信息进行回归。

model = Sequential()
model.add(LSTM(units=256, input_shape=(None, nFeature), dropout=0.5, return_sequences=True))
model.add(LSTM(units=256, dropout=0.5, return_sequences=False))
model.add(Dense(64, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1, kernel_initializer="uniform", activation='linear'))
model.compile(loss='mse', optimizer='Adam')

在这个较大的模型中，为了防止过拟合训练集和验证集，我采取了以下的措施：
在全连接(Dense)层和LSTM层中，加入Dropout。在训练中，dropout掉近似50%的参数，可以将网络模型减小至一半。在实验发现，减小至该网络一半的网络更不容易出现过拟合的情况（下文中会详细说明）。

提前结束训练(Early-stopping)。在两个相同的网络中，改变MN(即nPredict)的值，得到如下的测试集RMSE~epochs。由此可见，Early-stopping是非常有必要的。

注：MN=20的同样模型RMSE最好达到0.00148。

参数调整

我没有进行大规模的网格搜索以确定最好的超参数，我主要调整了网络的规模。基本想法是先选择一个较大的网络，训练至过拟合，判断其有足够拟合数据的能力，然后减小网络规模或进行正则化，消除过拟合以保留足够的泛化能力。

大网络（units = 256）：

中网络（units = 128）：

小网络（units = 64）：

在实验中发现，三个网络均会产生过拟合的问题。但是很明显小网络的拟合能力不足（在更大的RSME开始出现过拟合），而大网络的拟合能力极其严重。于是我选择了中网络规模的网络——大网络+50%dropout。

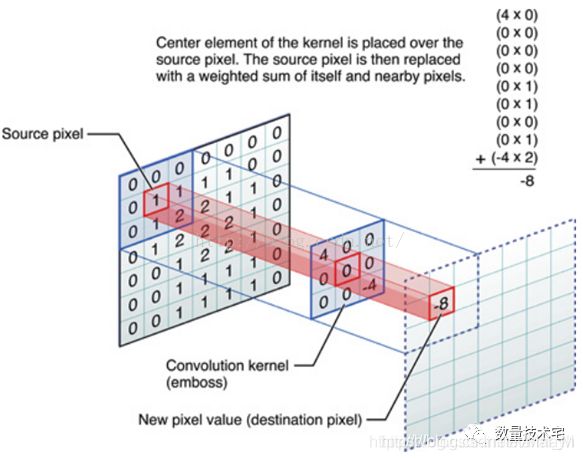
卷积神经网络

采取这个模型的主要原因是卷积神经网络模型可以通过共享(1,nFeature)卷积核减少参数，并将一组中每条数据进行同样地处理。

卷积神经网络由一个或多个卷积层和顶端的全连通层（对应经典的神经网络）组成，同时也包括关联权重和池化层（pooling layer）。这一结构使得卷积神经网络能够利用输入数据的二维结构。与其他深度学习结构相比，卷积神经网络在图像和语音识别方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他深度、前馈神经网络，卷积神经网络需要考量的参数更少，使之成为一种颇具吸引力的深度学习结构。

模型实现

利用Keras框架，实现卷积神经网络模型。具体结构为两层卷积网络和三层Dense层网络。其中两层卷积网络分别为1 ∗ 7卷积核和10 ∗ 1卷积核。

model = Sequential()
model.add(Conv2D(input_shape=(10,7,1),filters = 256, kernel_size = (1,7), strides=(1, 1), padding='valid',activation='relu'))
model.add(Dropout(0.5))
model.add(Conv2D(filters = 256, kernel_size = (10,1), strides=(1, 1), padding='valid',activation='relu'))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(512,kernel_initializer="glorot_normal",activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(256,kernel_initializer="glorot_normal",activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1,kernel_initializer="uniform",activation='linear'))
model.compile(loss='mean_squared_error', optimizer='Adam')

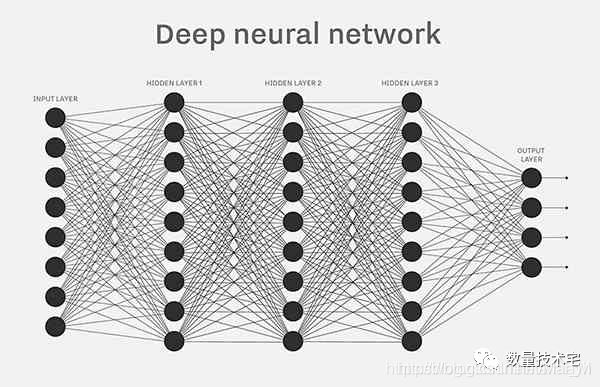
全链接的神经网络模型

神经网络模型的主要优点是具有极强的近似能力：模型可以以任意精度拟合一切连续函数。同时，进行这个模型的尝试，也可以判断卷积神经网络是否比朴素的全链接神经网络模型更好。

人工神经网络（英语：Artificial Neural Network，ANN），简称神经网络（Neural Network，NN）或类神经网络，在机器学习和认知科学领域，是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统，通俗的讲就是具备学习功能。现代神经网络是一种非线性统计性数据建模工具。

模型实现

model = Sequential()
model.add(Flatten(input_shape=(10,7,1)))
model.add(Dense(1024,kernel_initializer="glorot_normal",activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(512,kernel_initializer="glorot_normal",activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(256,kernel_initializer="glorot_normal",activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1,kernel_initializer="uniform",activation='linear'))
model.compile(loss='mean_squared_error', optimizer='Adam')

利用XGBoost创建的模型

XGBoost介绍

XGBoost代表“Extreme Gradient Boosting”，其中术语“Gradient Boosting”源于弗里德曼的贪婪函数逼近：梯度增强机。

XGBoost实质上是Gradient boosting Decision Tree(GBDT)的高效实现，如果使用最常用gbtree作为学习器，那么它基本相当于CART分类树。

CART分类回归树是一种典型的二叉决策树，可以做分类或者回归。如果待预测结果是离散型数据，则CART生成分类决策树；如果待预测结果是连续型数据，则CART生成回归决策树。数据对象的属性特征为离散型或连续型，并不是区别分类树与回归树的标准，例如表1中，数据对象xixi的属性A、B为离散型或连续型，并是不区别分类树与回归树的标准。作为分类决策树时，待预测样本落至某一叶子节点，则输出该叶子节点中所有样本所属类别最多的那一类（即叶子节点中的样本可能不是属于同一个类别，则多数为主）；作为回归决策树时，待预测样本落至某一叶子节点，则输出该叶子节点中所有样本的均值。

模型实现

利用xgboost库，实现XGB模型。

from xgboost import XGBRegressor
from sklearn.model_selection import GridSearchCV
cv_params = {'n_estimators': [600,800,1000,1200,1400,1600]}
other_params = {'learning_rate': 0.1, 'n_estimators': 100, 'max_depth': 4, 'min_child_weight': 5, 'seed': 0,
                    'subsample': 0.6, 'colsample_bytree': 0.9, 'gamma': 0.4, 'reg_alpha': 0, 'reg_lambda': 1}
model = XGBRegressor(**other_params)
optimized_GBM = GridSearchCV(estimator=model, param_grid=cv_params,
                             scoring='neg_mean_squared_error', cv=3, verbose=3, n_jobs=5)
optimized_GBM.fit(X_train_70, y_train)

参数调整

利用上述GridSearchCV函数以及类似于Gibbs采样算法的思想，逐步调整参数。具体方法为：首先设置每个参数的取值区间。然后选取某个参数，将其设置为取值区间中等间距的几个点，进行训练模型进行验证，将最好的点设置为这个参数的值，然后选取其他参数，重复这一步，直到参数稳定。

但实验中，由于过拟合情况严重，n_estimators越大会导致近似情况更好，但同时会导致模型的泛化能力降低。于是我通过提交结果，选定了n_estimator=200。然后调整其他参数。

随机回归森林模型

简单来说，随机森林就是多个回归树的融合。随机森林的优势在于

1. 在没有验证数据集的时候，可以计算袋外预测误差（生成树时没有用到的样本点所对应的类别可由生成的树估计，与其真实类别比较即可得到袋外预测）。
2. 随机森林可以计算变量的重要性。
3. 计算不同数据点之间的距离，从而进行非监督分类。

模型实现

利用sklearn库提供的RandomForestRegressor。

from sklearn.ensemble import RandomForestRegressor
clf = RandomForestRegressor(
    oob_score = True,
    max_depth = 20,
    min_samples_split=20,
    min_samples_leaf=10,
    n_estimators=20,
    random_state=0,
    verbose=3)
clf.fit(X_train.reshape(-1,70),y_train.reshape((-1,)))

模型之外

特征工程的重要性远远超过模型的选取以及调参。在最初的尝试中，我只是简单的进行了数据归一化，得到的结果并不理想，很多次训练的RNN模型有RMSE>0.00155的情况。在认真探索每个数据特征的意义并根据它们的意义进行数据处理后，采取的模型几乎全部RMSE<0.00150。我想，思考特征的特点并思考如何利用是十分关键的。毕竟说白了，这些模型只是泛用函数拟合器。

未来的工作

• 丰富订单簿信息。可以获得AskPrice2, AskPrice3,… 以及AskVolumn2,AskVolumn3等丰富信息。
• 采取更多的输入时间点。毕竟过去的数据是“免费”的，我们可以采用如过去一分钟的数据进行预测。但可能结果和MN的情况一样——再多的数据只是噪声。
• 丰富数据集。用更多股票和更长时间的数据。RNN模型的泛化能力没有被完全利用，我想通过更多的数据可以达到更好的效果。
  尝试XGboost的精细调参。
• 模型融合。如XGBoost+LightGBM+LSTM。