深度学习目标检测之 R-CNN 系列:Faster R-CNN 网络详解
深度学习目标检测之 R-CNN 系列:Faster R-CNN 网络详解
深度学习目标检测之 R-CNN 系列包含 3 篇文章:
- 深度学习目标检测之 R-CNN 系列: 从 R-CNN 和 Fast R-CNN 到 Faster R-CNN 总览
- 深度学习目标检测之 R-CNN 系列:Faster R-CNN 网络详解
- 深度学习目标检测之 R-CNN 系列:用 Faster R-CNN 训练自己的数据(caffe 版)
1. 前言
为了深入了理解 Faster R-CNN,这里建议参考 simple-faster-rcnn-pytorch 中的代码.
2. Faster R-CNN 网络概览
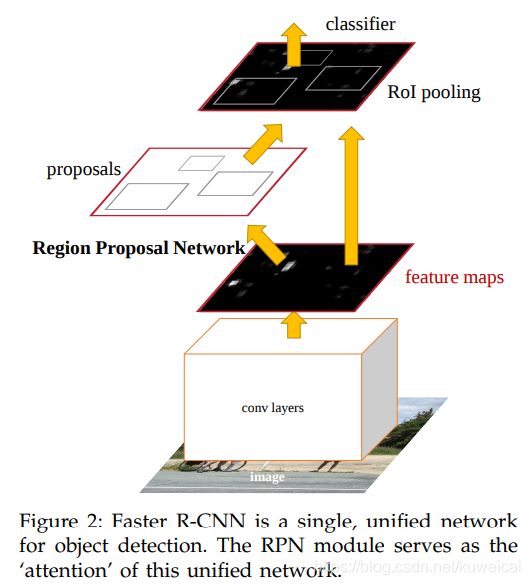
下图大致描述了 Faster R-CNN 的过程。
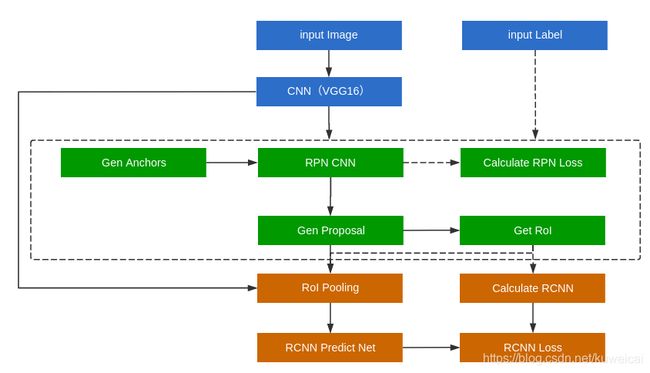
下面这幅图可能更清楚的表达了 Faster R-CNN 是如何工作的。只是需要注意的是下图是 test 网络。
更具体的过程可以参考下图。
-
- 将图片输入 CNN 网络(比如 ZF/VGG 等预训练好的分类模型),得到 feature maps;
-
- 将 feature maps 喂入 RPN(Region Proposal Network) 网络得到 region proposals (包含第一次回归)。更具体的,RPN 首先生成一堆Anchor box,对其进行裁剪过滤后通过 softmax 判断 anchors 属于前景(foreground)或者背景(background),即是不是物体,所以这是一个二分类任务;同时,另一分支 bounding box regression 修正(回归) anchor box,形成较精确的 proposal,注意这并是最后得到的 proposal,后面还会再进行第二次回归;
-
- 将上两步的输出:feature maps 和 region proposals 喂入 RoI Pooling 层得到统一 size 的 feature maps;
-
- 将 3 输出的 feature maps 输入全连接层,利用 Softmax 进行具体类别的分类,同时利用 L1 Loss 完成 bounding box regression 回归(第二次回归)操作获得物体的精确位置。
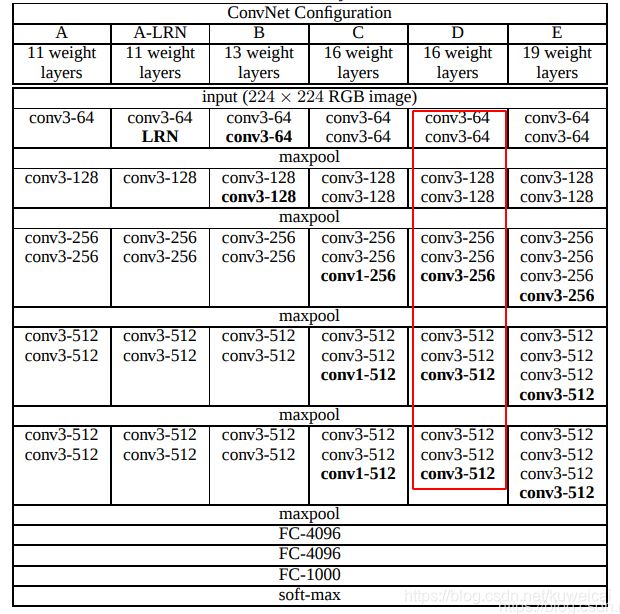
3. CNN
这里的 CNN 网络也可以叫做 conv layers,因为就是 conv + ReLU + Pooling 的组合,是没有 fc 层的。以 VGG16(13 个 conv + 3 个 fc) 为例,这里仅仅保留了其 13 个 conv 层,另外只保留了 4 个 Pooling 层,所以网络的 stride 为 16。
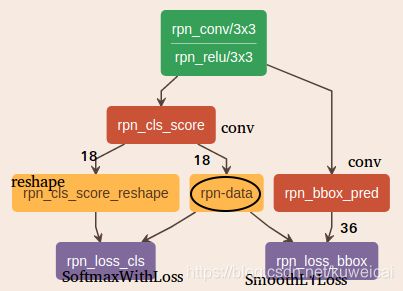
4. RPN
下图是 RPN 网络图,通过两个 1x1 的卷积层(conv)将 feature map 的 channel 分别变为 18 和 36,分别用来做分类和 bonding box 回归。这里面最为关键的 layer 就是 rpn-data,几乎所以核心的功能也都是在这个 layer 中完成。
RPN 网络具体的计算流程如下图所示。
总的来说,RPN 输入为 feature map, bbox 的标签(即训练集中所有物体的类别与 bbox 的位置),输出 proposal, 分类 loss,回归 loss。
值得注意的是这里预测的不是 bbox 的坐标,而是预测的相对于 Anchor 的偏移量。显然如果直接预测坐标,由于坐标变化幅度大,网络很难收敛与准确预测。
4.2 分类 loss
对于 RPN 而言就是一个二分类(前景和背景分类),采用的损失函数为交叉熵损失函数。
4.3 BBox 回归
假设我们对 anchor a 进行回归得到 predicated bbox p,那我们归一化的目标是希望 p 无限接近于 ground true(标记的结果)t。
在二维平面上,从矩形框 p 变换到矩形框 t,显然就是平移和缩放操作。假设 x , y , w , h x, y, w, h x,y,w,h 分别为 p 的中心坐标及宽和高; x a , y a , w a , h a x_a, y_a, w_a, h_a xa,ya,wa,ha 分别为 a 的中心坐标及宽和高; x ∗ , y ∗ , w ∗ , h ∗ x^*, y^*, w^*, h^* x∗,y∗,w∗,h∗ 分别为 t 的中心坐标及宽和高。那么从 p 到 a 的变换可以表示如下。
{ x = x a + ∇ x y = y a + ∇ y w = w a ⋅ ∇ w h = h a ⋅ ∇ h \left\{ \begin{aligned} & x = x_a +\nabla x\\ & y = y_a +\nabla y\\ & w = w_a \cdot \nabla w\\ & h = h_a \cdot \nabla h\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x=xa+∇xy=ya+∇yw=wa⋅∇wh=ha⋅∇h
上面的 ∇ \nabla ∇ 部分都是基于 w , h w, h w,h 计算出来的,表示如下。
{ ∇ x = w a ⋅ t x ∇ y = h a ⋅ t y ∇ w = w a ⋅ e t w ∇ h = h a ⋅ e t h \left\{ \begin{aligned} & \nabla x = w_a \cdot t_x\\ & \nabla y = h_a \cdot t_y\\ & \nabla w = w_a \cdot e^{t_w}\\ & \nabla h = h_a \cdot e^{t_h}\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∇x=wa⋅tx∇y=ha⋅ty∇w=wa⋅etw∇h=ha⋅eth
其中 t x , t y , t w , t h t_x, t_y, t_w, t_h tx,ty,tw,th 是预测的偏移量。根据上面的两个式子可以将其表示如下。
{ t x = x − x a w a t y = y − y a h a t w = l o g ( w w a ) t h = l o g ( h h a ) \left\{ \begin{aligned} & t_x = \frac {x-x_a}{w_a}\\ & t_y = \frac {y-y_a}{h_a}\\ & t_w = log(\frac {w}{w_a})\\ & t_h = log(\frac {h}{h_a})\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧tx=wax−xaty=hay−yatw=log(waw)th=log(hah)
同理。
{ t x ∗ = x ∗ − x a w a t y ∗ = y ∗ − y a h a t w ∗ = l o g ( w ∗ w a ) t h ∗ = l o g ( h ∗ h a ) \left\{ \begin{aligned} & t^*_x = \frac {x^*-x_a}{w_a}\\ & t^*_y = \frac {y^*-y_a}{h_a}\\ & t^*_w = log(\frac {w^*}{w_a})\\ & t^*_h = log(\frac {h^*}{h_a})\\ \end{aligned} \right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧tx∗=wax∗−xaty∗=hay∗−yatw∗=log(waw∗)th∗=log(hah∗)
这里需要注意下面几个问题:
-
为什么上面要用到 e 或 者 l o g e 或者 log e或者log,上面可以看到 e e e 用来表示 scale 系数,显然 scale 系数应该大于零,所以用 e e e 表示正好可以满足,那为什么用 l o g log log 呢? l o g log log 一个很重要的特性就是压缩大值,也就是说采用这种 loss 可以减小大的目标的作用,这样可以改善模型只能学到大的目标的缺点。
-
对于 x , y x,y x,y 采用的是线性变化,但是对于 w , h w, h w,h 却是用的非线性变化,这样合理吗?其实当 a 趋近于 t 时,可以认为 l o g log log 是线性变化。
4.4 Smooth L1 Loss
Smooth L1 Loss 的数学表达式如下。
f ( x ) = { 0.5 x 2 , ∣ x ∣ < 1 ∣ x ∣ − 0.5 , x < − 1 o r x > 1 f(x)=\left\{ \begin{aligned} & 0.5x^2, \space |x| < 1 \\ & |x| -0.5, \space x < -1 \space or \ x > 1 \\ \end{aligned} \right. f(x)={0.5x2, ∣x∣<1∣x∣−0.5, x<−1 or x>1
对于边框预测回归问题,通常也可以选择平方损失函数( L2 损失),但 L2 范数的缺点是当存在离群点(outliers) 的时候,这些点会占 loss 的主要组成部分。比如说真实值为1,预测 10 次,有一次预测值为 1000,其余次的预测值为 1 左右,显然 loss 值主要由1000 主宰。所以 Fast RCNN 采用稍微缓和一点的绝对损失函数(smooth L1损失),它是随着误差线性增长,而不是平方增长。
注意:smooth L1 和 L1-loss 函数的区别在于,L1-loss 在 0 点处导数不唯一,可能影响收敛。smooth L1 的解决办法是在 0 点附近使用平方函数使得它更加平滑。
更多内容可以参考 损失函数:L1 loss, L2 loss, smooth L1 loss。
5. RoI Pooling
ROI Pooling 的作用是将 RPN 输出的 region proposal 转换到相同的 size,然后再喂入 fc 层。RoI Pooling 还有一个进化版本 RoI Align。关于RoI Pooling 和 RoI Align 的介绍可以参考 ROI Pool和ROI Align。
6. 损失函数
Faster R-CNN 总共有四个损失函数,RPN 的分类和回归损失函数, Fast R-CNN 的分类和回归损失函数。RPN 的损失函数上面已经讲过,Fast R-CNN 的损失函数类似。Fast R-CNN 的分类损失为多分类交叉损失, 回归损失依然为 smooth L1 loss。
L ( p i , t i ) = 1 N c l s ∑ i L c l s ( p i , p i ∗ ) + λ 1 N r e g ∑ i p i ∗ L r e g ( t i , t i ∗ ) L({p_i},{t_i})= \begin{aligned} & \frac{1}{N_{cls}} \sum_iL_{cls}(p_i, p_i^*) +\lambda \frac{1}{N_{reg}} \sum_ip_i^*L_{reg}(t_i, t_i^*) \\ \end{aligned} L(pi,ti)=Ncls1i∑Lcls(pi,pi∗)+λNreg1i∑pi∗Lreg(ti,ti∗)
更为详细的介绍可以参考 [https://blog.csdn.net/Mr_health/article/details/84970776](Faster RCNN 损失函数理解).
7. Anchor 的压缩
在整个过程中对 Anchor 进行了多次压缩,分别如下:
- 在最开始划分 anchor 的时候,忽略超出边界的 anchor,大约 17000 个左右;
- 在 RPN 中进行 GT 匹配时,按照 background(与所有 GT 的最大 iou < 0.3)和 foreground(iou > 0.7) 划分时,忽略介于 0.3 和 0.7 之间的 anchor(标记为 -1);
- 对每一个预测为 foreground 的 anchor 的 score,进行排序,保留排名考前的大约 12000 个 anchor;
- 非极大值抑制(NMS),首先找到 score 最高的 anchor,然后以此 anchor 作为基准,计算其他的 anchor 与这个 anchor 的 iou,如果 iou 大于阈值,就认为是同一个目标,直接舍弃这个 anchor,最后大约剩余 2000 个左右的 anchor。
- 2000 个 anchor 中依然有很多副样本,通过 IoU (大于等于 0.5 为正样本,否则为负样本),最后选择 256 个正负样本(RoI),基本保持 3:1 的比例。