RepVGG论文笔记
文章目录
-
- RepVGG个人笔记
-
- 前言
- RepVGG模型
-
- 2.1主要架构
- 2.2RepVGG Block构造
- 2.3为什么构造RepVGG
-
- 2.3.1更快的速度
- 2.3.2更节省内存
- 2.3.3更加灵活
- 方法论:多分支融合
-
- 3x3卷积和1x1卷积融合
-
- identity分支等效特殊权重卷积层
- 卷积+BN融合
- 参考文章
RepVGG个人笔记
前言
RepVGG是一种简单的VGG式结构,大量使用3x3卷积,BN层,Relu激活函数,利用重参数化提升性能,准确率直逼其他SOTA网络,特点是训练时使用多分支网络,推理时融合多分支为单分支。
RepVGG模型
2.1主要架构
RepVGG模型的整体结构:将20多层3x3卷积堆起来,分成5个stage,每个stage的第一层是stride=2的降采样,每个卷积层用ReLU作为激活函数。
RepVGG模型的详细结构:RepVGG-A的5个stage分别有**[1, 2, 4, 14, 1]层,RepVGG-B的5个stage分别有[1, 4, 6, 16, 1]层,宽度是[64,128, 256, 512]**的若干倍。
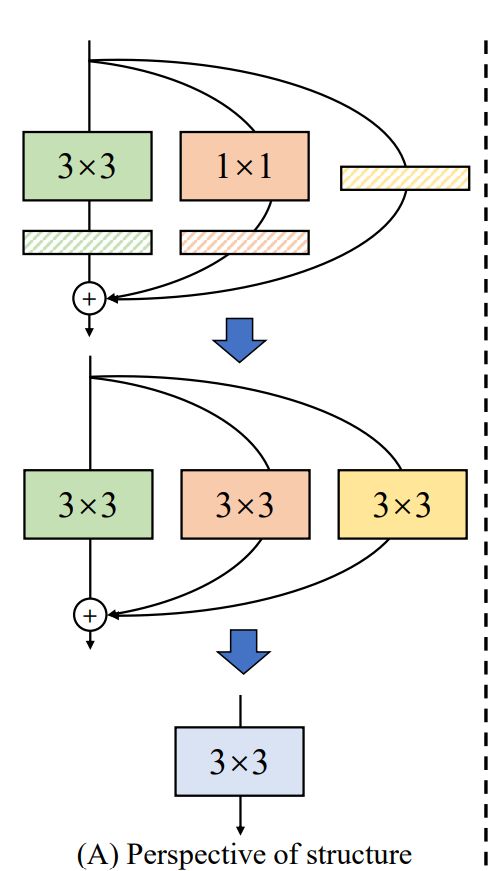
2.2RepVGG Block构造
训练时,为每一个3x3卷积层添加平行的1x1卷积分支和恒等映射分支,构成一个RepVGG Block。借鉴ResNet的做法,区别在于ResNet是每隔两层或三层加一分支,RepVGG Block是每层都加。
部署时,我们将1x1卷积分支和恒等映射分支以及3x3卷积融合成一个3x3卷积达到单路结构的目的。
2.3为什么构造RepVGG
2.3.1更快的速度
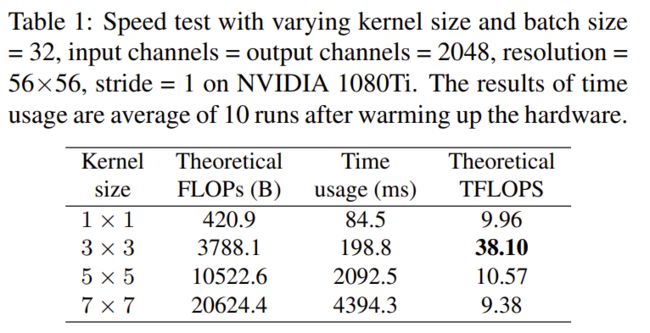
现有的计算库(如CuDNN,Intel MKL)和硬件针对3x3卷积有深度的优化,相比其他卷积核,3x3卷积计算密度更高,更加有效。
2.3.2更节省内存
以残差块结构为例子,它有2个分支,其中主分支经过卷积层,假设前后张量维度相同,我们认为是一份显存消耗,另外一个旁路分支需要保存初始的输入结果,同样也是一份显存消耗,这样在运行的时候是占用了两份显存,直到最后一步将两个分支结果Add,显存才恢复成一份。而Plain结构只有一个主分支,所以其显存占用一直是一份。RepVGG主体部分只有一种算子:3x3卷积接ReLU。在设计专用芯片时,给定芯片尺寸或造价,我们可以集成海量的3x3卷积-ReLU计算单元来达到很高的效率。单路架构省内存的特性也可以帮我们少做存储单元.
2.3.3更加灵活
多分支结构会引入网络结构的约束,比如Resnet的残差结构要求输入和卷积出来的张量维度要一致(这样才能相加),这种约束导致网络不易延伸拓展,也一定程度限制了通道剪枝。对应的单路结构就比较友好,剪枝后也能得到很好的加速比。
方法论:多分支融合
3x3卷积和1x1卷积融合
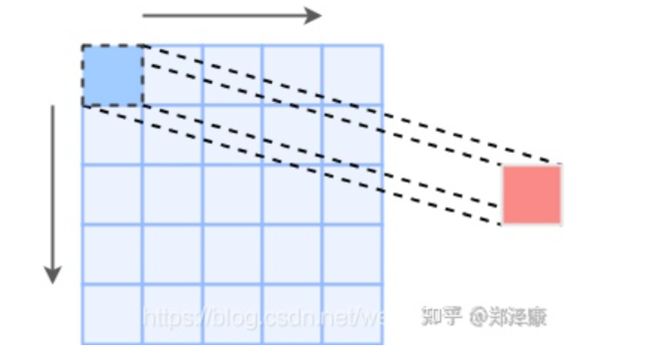
假设输入是5x5,stride=1
1x1卷积前后特征图大小不变
3x3卷积在原特征图补零,卷积前后特征图大小不变
将1x1卷积核加在3x3卷积核中间,就能完成卷积分支融合
融合示例图如下:
identity分支等效特殊权重卷积层
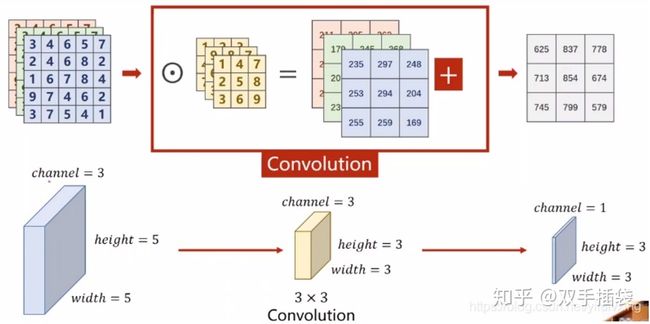
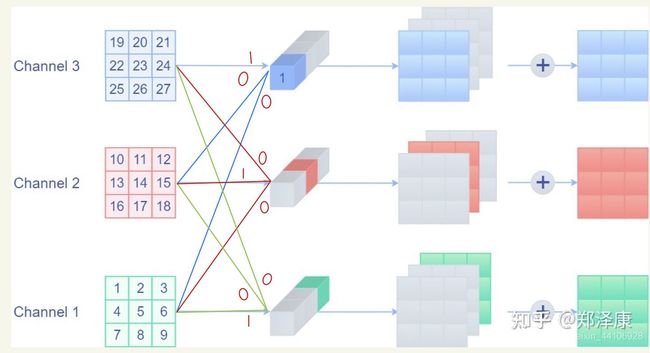
我们试想一下,输入与输出要相等,假设输入输出都是三通道
即每一个卷积核的通道数量,必须要求与输入通道数量一致,因为要对每一个通道的像素值要进行卷积运算,所以每一个卷积核的通道数量必须要与输入通道数量保持一致。
那么要保持原有三通道数据各权重应该如何初始化呢?
一个卷积核的尺寸为3x3x3,将对应通道的权重设为1其他为零,就能完好的保证输出原有值。
卷积+BN融合
在将identity分支和1x1卷积融合到3x3卷积后,我们将BN层融到卷积中去
在融合之前我们来了解一下Batch Norm
Batch-Normalization (BN)是一种让神经网络训练更快、更稳定的方法(faster and more stable)。它计算每个mini-batch的均值和方差,并将其拉回到均值为0方差为1的标准正态分布。BN层通常在nonlinear function的前面/后面使用。
I n p u t : V a l u e s o f x o v e r a m i n i − b a t c h : B = { x 1 … m } ; P a r a m e t e r s t o b e l e a r n e d : γ , β O u t p u t : { y i = B N γ , β ( x i ) } μ B ← 1 m ∑ i = 1 m x i ⋯ ⋅ ( 1 ) / / m i n i − b a t c h m e a n σ B 2 ← 1 m ∑ i = 1 m ( x i − μ B ) 2 − ⋯ ( 2 ) m i n i − b a t c h v a r i a n c e x ^ i ← x i − μ B σ B 2 + ϵ ⋯ ( 3 ) n o r m a l i z e y i ← γ x ^ i + β ≡ B N γ , β ( x i ) ⋯ ( 4 ) / / s c a l e a n d s h i f t Input: Values\ of \ x \ over\ a\ mini-batch:\\ \mathcal{B}=\left\{x_{1 \ldots m}\right\} ; Parameters to be learned: \gamma, \beta Output: \left\{y_{i}=\mathrm{BN}_{\gamma, \beta}\left(x_{i}\right)\right\} \\ \mu_{\mathcal{B}} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i} \quad \cdots \cdot(1) \quad \quad / / mini-batch mean\\ \sigma_{\mathcal{B}}^{2} \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2}-\cdots(2) mini-batch variance\\ \widehat{x}_{i} \leftarrow \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \cdots(3) normalize\\ y_{i} \leftarrow \gamma \widehat{x}_{i}+\beta \equiv \mathrm{BN}_{\gamma, \beta}\left(x_{i}\right) \cdots(4)//scale\ and\ shift Input:Values of x over a mini−batch:B={x1…m};Parameterstobelearned:γ,βOutput:{yi=BNγ,β(xi)}μB←m1i=1∑mxi⋯⋅(1)//mini−batchmeanσB2←m1i=1∑m(xi−μB)2−⋯(2)mini−batchvariancex i←σB2+ϵxi−μB⋯(3)normalizeyi←γx i+β≡BNγ,β(xi)⋯(4)//scale and shift
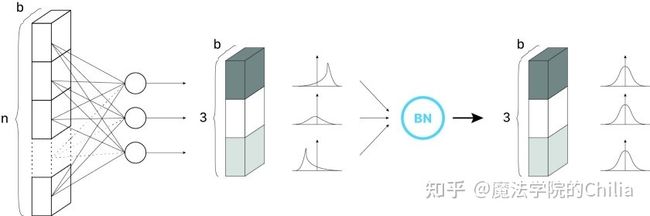
原文的公式可能不太好理解,引入图解来解释他的作用:
首先,用(1)(2)式计算一个mini-batch之内的均值和方差
然后,用(3)式来进行normalize。这样,每个神经元的output在整个batch上是标准正态分布,在全连接网络中是对每个神经元进行归一化,也就是每个神经元都会学习一个γ和β;在CNN中应用时,需要注意CNN的参数共享机制。每层有多少个卷积核,就学习几个γ和β进行线性变换。
那么融合过程是怎样的呢?
训练的时候,均值mean、方差var、γ 、β是一直在更新的,但是,在推理的时候,以上四个值都是固定了的,也就是推理的时候,均值和方差来自训练样本的数据分布。因此,在推理的时候,上面BN的计算公式可以变形为:
y i = γ x i − μ σ 2 + ε ) + β = γ σ 2 + ε x i + ( β − γ μ σ 2 + ε ) ) ) y_{i}=\gamma \frac{x_{i}-\mu}{\left.\sqrt{\sigma^{2}+\varepsilon}\right)}+\beta=\frac{\gamma}{\sqrt{\sigma^{2}+\varepsilon}} x_{i}+\left(\beta-\frac{\gamma \mu}{\left.\left.\sqrt{\sigma^{2}+\varepsilon}\right)\right)}\right) yi=γσ2+ε)xi−μ+β=σ2+εγxi+(β−σ2+ε))γμ)
令 a = γ σ 2 + ε , b = β − γ μ σ 2 + ε 那 么 在 均 值 m e a n 、 方 差 v a r 、 γ 、 β 都 是 固 定 值 的 时 候 B N 就 是 一 个 线 性 变 换 y = a x i + b 令a=\frac{\gamma}{\sqrt{\sigma^{2}+\varepsilon}}, b=\beta-\frac{\gamma \mu}{\sqrt{\sigma^{2}+\varepsilon}}\\那么在均值mean、方差var、γ 、β都是固定值的时候BN就是一个线性变换\\y=ax_{i}+b 令a=σ2+εγ,b=β−σ2+εγμ那么在均值mean、方差var、γ、β都是固定值的时候BN就是一个线性变换y=axi+b
引入一个三个神经元输入的全连接网络实例方便理解:
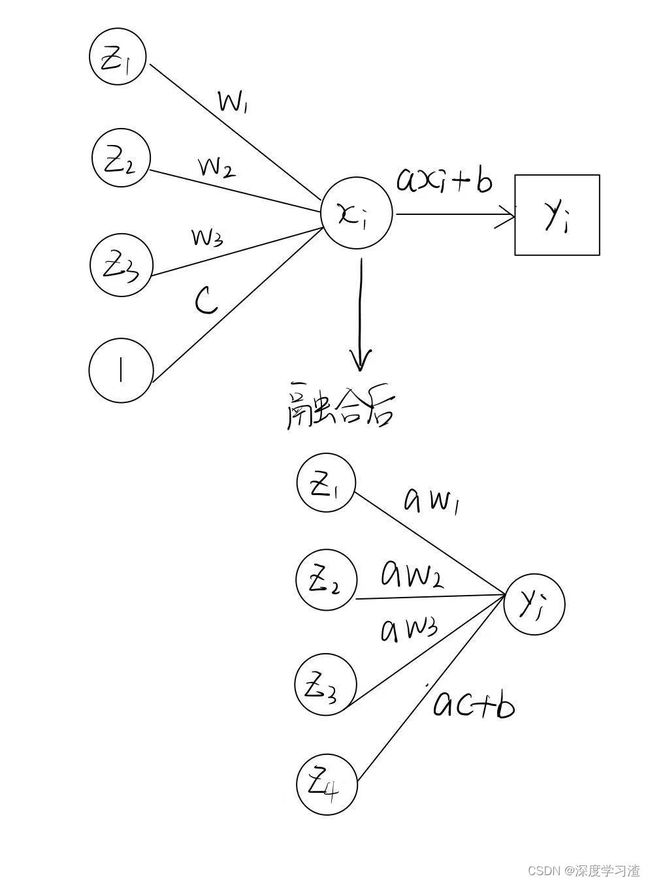
x i = w 1 ⋅ z 1 + w 2 ⋅ z 2 + w 3 ⋅ z 3 + c y i = a x i + b = a ( w 1 ⋅ z 1 + w 2 ⋅ z 2 + w 3 ⋅ z 3 + c ) + b y i = a w 1 ⋅ z 1 + a w 2 ⋅ z 2 + a w 3 ⋅ z 3 + ( a c + b ) x_{i}=w_{1} \cdot z_{1}+w_{2} \cdot z_{2}+w_{3} \cdot z_{3}+c\\ y_{i}=a x_{i}+b=a\left(w_{1} \cdot z_{1}+w_{2} \cdot z_{2}+w_{3} \cdot z_{3}+c\right)+b\\ y_{i}=a w_{1} \cdot z_{1}+a w_{2} \cdot z_{2}+a w_{3} \cdot z_{3}+(a c+b) xi=w1⋅z1+w2⋅z2+w3⋅z3+cyi=axi+b=a(w1⋅z1+w2⋅z2+w3⋅z3+c)+byi=aw1⋅z1+aw2⋅z2+aw3⋅z3+(ac+b)
参考文章
基础 | BatchNorm详解 - 知乎 (zhihu.com)
图解RepVGG - 知乎 (zhihu.com)
RepVGG 论文详解 - 知乎 (zhihu.com)
RepVGG:极简架构,SOTA性能,让VGG式模型再次伟大(CVPR-2021) - 知乎 (zhihu.com)
(25条消息) CNN卷积核与通道讲解_奥卡姆的剃刀的博客-CSDN博客_cnn卷积核
-2021) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/344324470)
(25条消息) CNN卷积核与通道讲解_奥卡姆的剃刀的博客-CSDN博客_cnn卷积核
(25条消息) 深度学习CNN网络推理时Batchnorm层和卷积层的融合,以提升推理速度。_songlixiangaibin的博客-CSDN博客