[翻译]C#数据结构与算法 – 第五章栈与队列(Part 1)
第5章栈与队列
以列表组织数据是很自然的方式。之前我们使用Array与ArrayList将数据作为列表组织。虽然这些数据结构帮助我们将数据以一种适合处理的格式组织,但没有一种结构提供了一种真实的抽象来实际地设计与实现问题的解决方案。
栈与队列是两种面向列表数据结构,其提供了易于理解的抽象。栈中的数据添加与移除都是由列表的一端进行,而队列中的数据由列表的一端添加并由列表的另一端移除。栈在编程语言的实现中广泛使用,从表达式评估到函数调用等一切问题。队列用于处理操作系统进程的优先级调用及模拟显示世界中事件的发生,如银行的收银台及大楼中的电梯操作。
C#提供了两个类来使用这两个数据结构:Stack类与Queue类。我们将讨论怎样使用这些类然后看一下本章中一些实际的例子。
栈,栈的实现与STACK类
栈是最常使用的数据结构,就像我们刚刚提到的那样。我们将栈定义为一个项目的列表,其仅可以由列表的尾部访问,这个尾部我们称为栈的顶部。一个栈的标准模式就像一个自助餐厅的一摞餐盘。盘子总是由一摞的顶部被取走,当洗碗工或服务生把盘子放回时,仍然是放回顶部。栈是一种被称作后进先出(LIFO)的数据结构。
栈操作
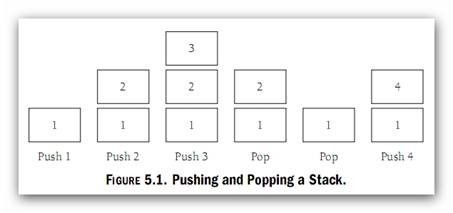
栈的两个最主要操作是向栈添加项与由栈中移除项。Push操作向栈中添加一个项,Pop操作由栈中移除一个项。图5.1展示了这些操作。
另一个在栈上完成的主要操作是查看顶部元素。Pop操作虽返回顶部元素,但是此操作也将这个元素由栈顶部移除。我们仅是要在不移除其的情况下来查看顶部的元素。在C#中这个操作名为Peek,在其他语言或实现中这个名称可能不同(如为Top)。
Push,Pop与Peek是使用栈时我们进行的主要操作;同时,还有许多其它的方法及属性需要我们学习并尝试操作。由一个栈中一次移除所有项是很有用的。通过调用Clear操作可以将一个栈完全清空。随时可以获取到栈中项的数目也是很有用的。通过调用Count属性可以实现这个目的。许多操作都通过一个返回true或false的StackEmpty方法来判断栈的状态,我们也可以使用Count属性实现同样的目的。
.NET Framework中的Stack类实现了以上提到的这些以及更多的属性与方法,但是在我们学习使用Stack之前,先来了解一下如果没有Stack类,我们怎样实现一个栈。
一个栈类的实现
一个栈的实现需要使用底层的数据结构来存储数据。我们将选择ArrayList因为这样做我们就无需为当新项被入栈时调整列表的大小而发愁。
由于C#拥有极好的面向对象编程的特性,我们将这个栈实现为一个类,称作CStack。这个类中我们将实现一个构造函数,上面提到的那些方法以及Count这个属性以展示怎样在C#中完成这个工作。
首先让我们实现这个类中需要的私有数据成员。
这个类中最主要的变量是一个用来存储栈项目的ArrayList对象。我们需要跟踪的仅有的另一个数据是栈的顶部,我们将用一个简单的整型变量来用作索引。这个变量在一个CStack对象初始化时被设置为-1,每当一个项目被压入栈,这个变量将增1。
构造函数除了将索引变量初始化-1外不再做其它工作。第一个要实现的方法是Push,其代码调用ArrayList的Add方法将要添加的值传递给ArrayList。Pop方法完成3个工作:首先调用RemoveAt方法取得栈顶部元素(并由ArrayList中移除),将索引值减1,最后,返回出栈的对象。
Peek方法的实现可以通过Item索引器并使用索引变量作为参数获取所需的值。Clear方法简单调用了ArrayList类中等价的方法。Count属性被实现为一个只读属性,因为我们不希望不小心更改了栈中项的数目。
如下是完成的代码:
1 class CStack 2 { 3 private int p_index; 4 private ArrayList list; 5 6 public CStack() 7 { 8 list = new ArrayList(); 9 p_index = -1; 10 } 11 12 public int count 13 { 14 get { return list.Count; } 15 } 16 17 public void push(object item) 18 { 19 list.Add(item); 20 p_index++; 21 } 22 23 public object pop() 24 { 25 object obj = list[p_index]; 26 list.RemoveAt(p_index); 27 p_index--; 28 return obj; 29 } 30 31 public void clear() 32 { 33 list.Clear(); 34 p_index = -1; 35 } 36 37 public object peek() 38 { 39 return list[p_index]; 40 } 41 }
接下来让我们使用这段代码完成一个使用栈解决问题的程序。
回文是一种正向与反向拼写都相同的字符串。如:”dad”,”madam”与”sees”都是回文,而像”hello”就不是回文。一种检查字符串是否为回文的方式就是使用栈。一般的算法是逐个字符的读取字符串并在读取时将每个字符如栈。这起到了一个将字符串字符反向保存的效果。下一步是将每一个字符出栈,同时由原始字符串开始处比较相应的字符。如果在任何位置两个字符不相同,字符串就不是一个回文,程序就可以停止。如果比较可以从头进行到尾,这个字符串就是一个回文。
如下是程序,只列出Main函数,因为我们已定义了CStack类:
1 static void Main(string[] args) 2 { 3 CStack alist = new CStack(); 4 string ch; 5 string word = "sees"; 6 bool isPalindrome = true; 7 8 for (int x = 0; x < word.Length; x++) 9 alist.push(word.Substring(x, 1)); 10 11 int pos = 0; 12 13 while (alist.count > 0) 14 { 15 ch = alist.pop().ToString(); 16 if (ch != word.Substring(pos, 1)) 17 { 18 isPalindrome = false; 19 break; 20 } 21 pos++; 22 } 23 24 if (isPalindrome) 25 Console.WriteLine(word + " is a palindrome."); 26 else 27 Console.WriteLine(word + " is not a palindrome."); 28 29 Console.Read(); 30 }
Stack类
Stack类是一个表现为LIFO的实现ICollection接口的集合类/栈。.NET Framework中的栈类被实现为一个循环缓冲器,其允许如栈的项所需的空间可以被动态分配。
Stack类中包含了用于入栈,出栈及获取栈顶值的方法。同样提供了获取栈中元素数目的属性,清空栈中值的方法,以及将栈转换为数组的方法。首先我们来研究一下Stack类的构造函数。
Stack类构造函数
有三种方式来初始化一个Stack对象。默认构造函数初始化一个空的栈并将Capacity属性初始化为10。默认构造函数以如下方式调用:
1 Stack myStack = new Stack();
一个泛型栈以如下方式初始化:
1 Stack<string> myStack = new Stack<string>();
每当栈中的元素数达到栈最大容量,容量会被加倍。
Stack的第二个构造函数允许你由另一个集合对象创建一个栈对象。例如,你可以向构造函数传递一个数组,一个栈将由已存在数组元素来创建:
1 string[] names = newstring[]{"Raymond","David", "Mike"}; 2 Stack nameStack = new Stack(names);
执行Pop方法将首先由栈中移除”Mike”。
你也可以在初始化一个栈对象的同时指定栈的初始容量。当你可以提前知道要在栈中存储多少个元素时这个构造函数就可以发挥作用。如果以这种方式来构建你的栈你可以使你的程序更高效。如果你的栈有20个元素并且已经达到最大容量,添加一个新元素将会触发20+1次操作,因为每一个元素都需要被移动来适应新的元素。
在初始化栈同时指定初始大小的代码如下:
1 Stack myStack = new Stack(25);
栈的主要操作
在栈上执行的主要操作为Push与Pop。使用Push方法将数据入栈。使用Pop方法完成数据出栈操作。让我们在使用栈计算简单的算术表达式这个问题环境中学习这些方法。
表达式求值程序使用两个栈,其中一个用于操作数,另一个用于运算符。一个算术表达式存储于被作为字符串存储。通过使用for循环读取表达式中的每个字符,我们将字符串分析为单独的符号。如果符号是一个数字,将其放入数字栈。如果符号是一个运算符,将其放入运算符栈。因为我们执行中缀表达式,在执行一个操作之前我们需要等待两个操作数入栈完成。在这一时刻,我们将两个操作数前后出栈并执行指定的算术运算。结果被重新入栈来作为下一次计算的第一个表达式。这个过程持续到我们对所有的数字完成入栈与出栈操作。
如下是代码:
1 using System; 2 using System.Collections; 3 using System.Text.RegularExpressions; 4 5 namespace csstack 6 { 7 class Class1 8 { 9 static void Main(string[] args) 10 { 11 Stack nums = new Stack(); 12 Stack ops = new Stack(); 13 string expression = "5 + 10 + 15 + 20"; 14 Calculate(nums, ops, expression); 15 Console.WriteLine(nums.Pop()); 16 Console.Read(); 17 } 18 19 // IsNumeric isn't built into C# so we must define it 20 static bool IsNumeric(string input) 21 { 22 bool flag = true; 23 string pattern = (@"^\d+$"); 24 Regex validate = new Regex(pattern); 25 if (!validate.IsMatch(input)) 26 { 27 flag = false; 28 } 29 return flag; 30 } 31 32 static void Calculate(Stack N, Stack O, string exp) 33 { 34 string ch, token = ""; 35 36 for (int p = 0; p < exp.Length; p++) 37 { 38 ch = exp.Substring(p, 1); 39 if (IsNumeric(ch)) 40 token += ch; 41 if (ch == " " || p == (exp.Length - 1)) 42 { 43 if (IsNumeric(token)) 44 { 45 N.Push(token); 46 token = ""; 47 } 48 } 49 else if (ch == "+" || ch == "-" || ch == "*" || ch == "/") 50 O.Push(ch); 51 if (N.Count == 2) 52 Compute(N, O); 53 } 54 } 55 56 static void Compute(Stack N, Stack O) 57 { 58 int oper1, oper2; 59 string oper; 60 oper1 = Convert.ToInt32(N.Pop()); 61 oper2 = Convert.ToInt32(N.Pop()); 62 oper = Convert.ToString(O.Pop()); 63 switch (oper) 64 { 65 case "+": N.Push(oper1 + oper2); 66 break; 67 case "-": N.Push(oper1 - oper2); 68 break; 69 case "*": N.Push(oper1 * oper2); 70 break; 71 case "/": N.Push(oper1 / oper2); 72 break; 73 } 74 } 75 } 76 }
使用Stack完成后缀表达式的算数计算更简单。在练习中你将有机会实现一个后缀表达式计算器。
Peek方法
Peek方法允许我们查看栈顶元素的值而无需将项由栈中移除。如果没有这个方法,当你需要获取栈顶项的值时你不得不将此项出栈。在你需要将项出栈之前你将需要此方法来查看栈顶元素的值:
1 if (IsNumeric(Nums.Peek())) 2 num = Nums.Pop();
Clear方法
Clear方法由栈中移除所有项目,将项的数目设置为0。很难讲Clear方法是否会影响栈的最大容量属性,因为我们无法查看栈的实际最大容量,所以最好假定栈的最大容量被设置回初始的默认大小—10个元素。
Clear方法的一个最大作用在处理过程中发生错误时清空一个栈。如,在我们的表达式求值程序中,如果发生除0操作,就是一个错误,我们需要清空栈:
1 if (oper2 == 0) 2 Nums.Clear();
Contains方法
Contains方法可以判断一个指定的元素是否位于栈中。如果元素被找到此方法返回true,反之返回false。我们可以用这个方法查找一个当前并不位于栈顶的值,如这种情况:可以判断一个会引起处理错误的字符是否存在于栈中:
1 if (myStack.Contains(" ")) 2 StopProcessing(); 3 else 4 ContinueProcessing();
CopyTo与ToArray方法
CopyTo方法将一个栈中的内容拷贝到一个数组。数组必须为Object类型,因为这是所有栈对象的数据类型。这个方法接受两个参数:一个数组及一个索引表示由数组中这个位置开始放置拷贝的元素。元素以LIFO的顺序被拷贝,就如它们被出栈的顺序一般。下面代码段展示了CopyTo方法的调用:
1 Stack myStack = new Stack(); 2 for (int i = 20; i > 0; i--) 3 myStack.Push(i); 4 object[] myArray = new object[myStack.Count]; 5 myStack.CopyTo(myArray, 0);
ToArray方法以一种类似的方式工作。你不可以在数组中指定一个起始位置,同时必须在赋值语句中创建一个新数组。见如下示例:
1 Stack myStack = new Stack(); 2 for (int i = 0; i > 0; i++) 3 myStack.Push(i); 4 object[] myArray = new object[myStack.Count]; 5 myArray = myStack.ToArray();
Stack类示例:十进制到多种进制转换
虽然商业应用中10进制数有广泛的使用,但部分科学与技术应用中需要数字以其它进制方式来表示。许多计算机系统应用需要8进制或2进制格式数字。
一种将十进制像二进制或八进制转换的算法是使用栈。算法步骤如下:
- 获取数字
- 获取进制
- 循环
- 将数字与进制的相除的余数入栈
- 将数字置为原数字除以进制后的整数部分
- 当数字不为0的情况下继续循环
当循环结束时,你需要转换数字,你可以简单的将单独的数字出栈来查看结果。下面的程序展示了一个实现:
1 using System; 2 using System.Collections; 3 4 namespace csstack 5 { 6 class Class1 7 { 8 static void Main(string[] args) 9 { 10 int num, baseNum; 11 Console.Write("Enter a decimal number: "); 12 num = Convert.ToInt32(Console.ReadLine()); 13 Console.Write("Enter a base: "); 14 baseNum = Convert.ToInt32(Console.ReadLine()); 15 Console.Write(num + " converts to "); 16 MulBase(num, baseNum); 17 Console.WriteLine(" Base " + baseNum); 18 Console.Read(); 19 } 20 21 static void MulBase(int n, int b) 22 { 23 Stack Digits = new Stack(); 24 do 25 { 26 Digits.Push(n % b); 27 n /= b; 28 } 29 while (n != 0); 30 31 while (Digits.Count > 0) 32 Console.Write(Digits.Pop()); 33 } 34 } 35 }
这个程序展示了为什么对于大部分计算机问题,栈是一个有用的数据结构。当我们将十进制向其它格式转换时,我们由最右端的数字开始一直向左计算。在这个过程中把每一个数字入栈,因为这样当计算结束时,转换后的数字将是正确的顺序。
虽然栈是一种有用的数据结构,一些程序的模型更适合其它基于列表类型的数据结构。例如:杂货店或周围的音像租赁商店中排的队。不像一个栈的后进先出的工作方式,队列中先进的应该先出(FIFO)。另一个例子是发送给一个网络(或本地)打印机的打印作业的列表。第一个发送给打印机的作业应该被第一个处理。这些例子被模型化一种称作队列的基于列表的数据结构,这是下一节的主题。