2022年MathorCup建模赛D题：MATLAB代码与若干问题

本笔记作于2022年4月19日晚。作者所在团队曾参加2022年4月的MathorCup数学建模赛，并选择D题。

按照cufe目前的培养方案，当前阶段（本科二年级）认真学过的代码是cpp，也有大数据与金融在讲python、金融数值计算在讲MATLAB、还有基于cpp的数据结构。所以在使用MATLAB的时候，也会或多或少受到cpp的影响。

代码1：MathorCup_Q1.m

总评：这个代码较为完整的解决了Question1，但是对于后续Question2的解决及其不友好，原因就在于做了过多的“删除”。

%以矩阵方式导入附录1(含第四行索引)、附录2，并命名为appendix1、appendix2
%筛选出距离小于等于10的点，第5列标记为1
for j = 1:1474
    id = find(((appendix1(:,1)-appendix2(j,2)).^2+(appendix1(:,2)-appendix2(j,3)).^2)<=100);
    appendix1(id,5)=1;
end
%做出基站位置和种类的决策
traffic=0;
TRAFFIC=7056230.115;
test=sortrows(appendix1,-3);%相当于Excel按某一列逆序排序
test(find(test(:,5)==1),:)=[];
appendix1(:,6)=0;%初始化，为了下面内层for循环不越界
while traffic/TRAFFIC<0.9
    myflag = 0;%预先为条件判定值设为外层循环局部变量
    for i=find(appendix1(:,6)~=0)%检查是否和新建站址间的距离不超过10
        distance = (appendix1(i,1)-test(1,1)).^2+(appendix1(i,2)-test(1,2)).^2;
        if distance<=100
            test(1,:)=[];
            myflag = 1;%为跳出两层嵌套循环，设立条件判定值myflag
            break
        end
    end
    if myflag == 1
        break
    end
    id1 = find(((appendix1(:,1)-test(1,1)).^2+(appendix1(:,2)-test(1,2)).^2)<=900);
    sum1 = sum(appendix1(id1,3),1);
    id2 = find(((appendix1(:,1)-test(1,1)).^2+(appendix1(:,2)-test(1,2)).^2)<=100);
    sum2 = sum(appendix1(id2,3),1);
    if sum1/10 >= sum2
        appendix1(find(appendix1(:,4)==test(1,4)),6)=2;
        test(find(ismember(test(:,4),id1)==1),:)=[];%按值属于集合id1删除
        traffic = traffic+sum1;
    else
        appendix1(find(appendix1(:,4)==test(1,4)),6)=1;
        test(find(ismember(test(:,4),id2)==1),:)=[];%按值属于集合id2删除
        traffic = traffic+sum2;
    end
end
total_pecent = traffic/TRAFFIC;
total_cost = sum(appendix1(:,6),1)*9-8;
appendix1(find(appendix1(:,6)==0),:)=[];
csvwrite('MathorCup_Q1.csv',appendix1)

代码说明：
事先按照matrix类型导入appendix1.csv和appendix2.csv。
appendix1.csv（182807个弱覆盖点）：
A列：x轴坐标 B列：y轴坐标 C列：traffic值 D列：索引（自行加上）
appendix2.csv（1474个已有基站）：
A列：id值 B列：x轴坐标 C列：y轴坐标

Question1算法和代码点评和问题

一、算法逻辑。我们的算法是仅在弱覆盖点进行基站布局。每次从traffic最大的弱覆盖点开始布局基站。每次布设完毕后，将该基站和所有其能覆盖的弱覆盖点从矩阵中删除，同时统计traffic的增加值。直到某次traffic之和已经超过了总traffic的90%，则停止布设。

一个很大的问题是，为何仅仅只在弱覆盖点进行基站布局。这是没办法的办法。
还有一个硬伤很大的问题，就是开始的时候不应该“删除”已经覆盖的点，而应该是做一个“标记”。因为一旦“删除”，很多后续的操作也就止步于此了。但是首先代码就是按照删来写的，所以后来庞大的代码没时间再做更改了。
这也涉及到以后写代码的一个思想：可删可不删的，坚决不删。

二、按照算法逻辑，MATLAB代码核心是一个while循环，条件是traffic/TRAFFIC<0.9。

三、关于两个matrix。这也是没有办法的办法，因为需要一个matrix实现“删除”，又需要一个matrix实现记录到底放宏基站还是微基站，以及那些弱覆盖点的位置被选定放基站。所以，我用test实现删除，用原来的appendix1实现记录。

我最后尝试，是否能简化为仅仅通过一个matrix来实现。但是涉及到构造新的一列来标记是否已被覆盖，还涉及到找matrix中第一个给定的列的给定条件的第一个值，涉及的代码更改量太大，所以作罢。这也说明代码一开始构思时的重要性。

Question1代码：MATLAB的相关小技巧

一、如何跳出两层循环——旗帜变量myflag

以下代码就解决了一个问题：检查是否和已有新建站址见的距离不超过10。

    myflag = 0;%预先为条件判定值设为外层循环局部变量
    for i=find(appendix1(:,6)~=0)%检查是否和新建站址间的距离不超过10
        distance = (appendix1(i,1)-test(1,1)).^2+(appendix1(i,2)-test(1,2)).^2;
        if distance<=100
            test(1,:)=[];
            myflag = 1;%为跳出两层嵌套循环，设立条件判定值myflag
            break
        end
    end
    if myflag == 1
        break
    end

很显然，如果出现小于等于10的情况，那就被pass掉了，不仅仅是要退出这里的for循环，还要退出外层的while traffic/TRAFFIC<0.9的循环。
但是一个break只能退出当前内层循环。
解决思路是涉及旗帜变量myflag，思路源于CSDN。

二、排序函数——sortrows

sortrows(appendix1,-3)函数，相当于Excel按某一列逆序排序的功能。

三、什么时候要进行初始化？

原因是MATLAB寻访矩阵元素的时候，一旦越界将会报错。
那为什么要进行appendix1(:,6)=0初始化，而不需要进行appendix1(:,5)=0初始化？
我们发现，对appendix1(:,5)的第一个操作是appendix1(id,5)=1;已经有了初始化的操作。
但是对appendix1(:,6)的第一个操作是find(appendix1(:,6)~=0)，是寻访。在没有初始化的情况下寻访，会报错。

四、如何实现按值存取和多表联立——兼谈find()和ismember()函数

包括MATLAB在内的多种语言都是按位存取，即按照索引index对数组/矩阵的相关元素进行读或写的操作。我们在数据结构课中认识到，在c++中实现线性表的按值存取需要for循环的逐一比对，时间复杂度为O(n)。
MATLAB的优势在于find()函数。底层算法保证了find()的时间复杂度远低于for循环。
这里的例子是，id1是可覆盖点在appendix1的索引，对应的是text中的第4列的值。但是因为对text进行删删删，所以id1中显然可能存在text中的第4列没有的那些东西。所以我需要一个函数来解决一个元素是否属于一个集合的问题。CSDN告诉我这个函数是ismember()。最终我采用的代码是

test(find(ismember(test(:,4),id1)==1),:)=[];%按值属于集合id1删除

事实上，这个代码可以简化为

test(ismember(test(:,4),id1),:)=[];

因为ismember()返回值是一个logical类型矩阵，能够被矩阵名test直接存取。
综上，MATLAB的直接存取至少有3种形式：
1、按位存取：如test(3,:)
2、按条件存取：如test(find(test(:3)>10000),:)，这其实是按值存取的一种推广，因为按值其实也是一种条件。事实上，在c++中实现按条件存取和按值存取的规则一样。
3、按布尔值存取：也可视为一种形式的按条件存取，但是test()括号中放的是logical类型矩阵。

五、关于Python和MATLAB底层的时间复杂度问题

MathorCup_Q1.m的运行大约花费17秒。
我们尝试用Python跑代码的前4行，即筛选出距离小于等于10的点。嵌套了2层for循环，分别要遍历182807次和1474次。这个代码跑完，大概要18个小时。

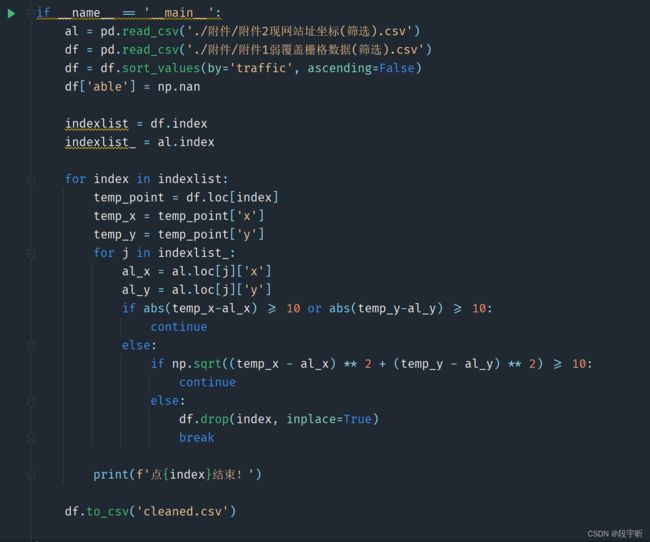
之所以MATLAB具有17秒和18小时相比的优势，我认为原因在于find()函数在底层大大降低了for循环的时间复杂度。MATLAB的底层逻辑是矩阵计算，find()函数并不是基于for循环遍历的底层算法。
也有一个所谓的原则，就是在MATLAB中尽可能少用for/while循环，而转用find()函数。但是我的MathorCup_Q1.m仍然存在不少的for/while循环。至少我没有一个很好的方式能将其简化为用find()函数的形式。

代码2：MathorCup_Q2.m

总评：首先改编了MathorCup_Q1，使的其对Q2更为兼容。改编就在于多设置了class_num变量和appendix1(:,7)用来记录类型。但是存在难以解释的疑问。在MathorCup_Q2中，由于MATLAB规划代码的不兼容性，这里的代码不能完整求解。

改编后的MathorCup_Q1.m

%以矩阵方式导入附录1(含第四行索引)、附录2，并命名为appendix1、appendix2
%满足门限要求：筛选出距离小于等于10的点，第5列标记为1
for j = 1:1474
    id = find(((appendix1(:,1)-appendix2(j,2)).^2+(appendix1(:,2)-appendix2(j,3)).^2)<=100);
    appendix1(id,5)=1;
end
%做出基站位置和种类的决策
traffic=0;
TRAFFIC=7056230.115;
test=sortrows(appendix1,-3);
test(find(test(:,5)==1),:)=[];
appendix1(:,6)=0;%初始化，为了下面内层for循环不越界
appendix1(:,7)=0;
class_num = 0;%预先设置类变量
while traffic/TRAFFIC<0.9
    myflag = 0;%预先为条件判定值设为外层循环局部变量
    for i=find(appendix1(:,6)~=0)%检查是否和新建站址间的距离不超过10
        distance = (appendix1(i,1)-test(1,1)).^2+(appendix1(i,2)-test(1,2)).^2;
        if distance<=100
            test(1,:)=[];
            myflag = 1;%为跳出两层嵌套循环，设立条件判定值myflag
            break
        end
    end
    if myflag == 1
        break
    end
    class_num = class_num+1;
    id1 = find(((appendix1(:,1)-test(1,1)).^2+(appendix1(:,2)-test(1,2)).^2)<=900);
    sum1 = sum(appendix1(id1,3),1);
    id2 = find(((appendix1(:,1)-test(1,1)).^2+(appendix1(:,2)-test(1,2)).^2)<=100);
    sum2 = sum(appendix1(id2,3),1);
    if sum1/10 >= sum2
        appendix1(find(appendix1(:,4)==test(1,4)),6)=2;
        appendix1(id1,7)=class_num;
        test(find(ismember(test(:,4),id1)==1),:)=[];%按值属于集合id1删除
        traffic = traffic+sum1;
    else
        appendix1(find(appendix1(:,4)==test(1,4)),6)=1;
        appendix1(id2,7)=class_num;
        test(find(ismember(test(:,4),id2)==1),:)=[];%按值属于集合id2删除
        traffic = traffic+sum2;
    end
end
total_pecent = traffic/TRAFFIC;
total_cost = sum(appendix1(:,6),1)*9-8;
csvwrite('MathorCup_Q1_1.csv',appendix1)
appendix1(find(appendix1(:,7)==0),:)=[];
csvwrite('MathorCup_Q1_2.csv',appendix1)
appendix1(find(appendix1(:,6)==0),:)=[];
csvwrite('MathorCup_Q1_3.csv',appendix1)

MathorCup_Q2.m

for i=1:1388
    mylist = testQ2(find(testQ2(:,5)==i),:);
    if length(mylist)==0
        break
    end
    if length(mylist)==1
        testQ2(i,6)=0;
        testQ2(i,7)=0;
        testQ2(i,8)=0;
        break
    end
    %alpha
    mylist(2:end,6)=atan((mylist(2:end,2)-mylist(1,2))./(mylist(2:end,1)-mylist(1,1)));
    %AT length
    mylist(2:end,7)=sqrt((mylist(2:end,2)-mylist(1,2)).^2+(mylist(2:end,1)-mylist(1,1)).^2);
    %target function
    fun=@(x)sum(find(ar(mylist(2:end,6),x(1))>mylist(2:end,7)&ar(mylist(2:end,6),x(2))>mylist(2:end,7)&ar(mylist(2:end,6),x(3))>mylist(2:end,7)),3);
    x0=rand(3,1);
    A=[];
    b=[];
    Aeq=[];
    beq=[];
    vlb=[0,0];
    vub=[];
    [x,fval]=fmincon(fun,x0,A,b,Aeq,beq,vlb,vub)
end

ar.m

function [myar]=ar(alpha ,theta)
if abs(alpha-theta)>pi/3
    myar = 0;
end
myar = 10-(15/pi)*abs(alpha-theta);

Question2存在的问题

一、运行出来的MathorCup_Q1_2.csv和MathorCup_Q1_3.csv中，如果按照第7列顺序排列，会发现断层和重排问题。
最明显的例子的就是没有第7类，再有如第125类就对应2个放了基站的点，即原序号为97172、97173的。
这个原因查清了，是因为
appendix1(id1,7)=class_num;
appendix1(id2,7)=class_num;
一句代码可能把之前已经归类的点进行了再次归类。我们应该把这种归类定义为非法的。当天是过生日，晚上喝了很多酒，想到的一种思路是把代码中的相应两句改为
appendix1(id1,7)=(appendix1(id1,7)==0).*class_num;
appendix1(id2,7)=(appendix1(id2,7)==0).*class_num;
这似乎是很聪明的更改方式，因为用简单的一行就实现了再次归类的避免操作。但是这一句犯了语法错误。appendix1(id1,7)==0是一个逻辑表达式，他的返回值是logistic型矩阵。它和double型矩阵class_num相乘时，会把原来appendix1(id1,7)非0的那些点全归位第0类。这是极大的错误。
投机取巧的方式报错。与其强求一行代码，解决问题，还不如多写几行，直接放一个if-else语句来得方便。这的确能解决这一问题。
而我曾想第6列只和为什么不是1388而是1490。其实是因为这里的宏基站值为2，是1490说明有102个宏基站，并不是错误。

二、MathorCup_Q1_2.csv的第3列的和只有5040329，远远达不到TRAFFIC的90%。这是为什么，我没有弄明白，按道理while循环的跳出条件就是达到90%呀。这里可能的问题应该是sum的计算和appendix1矩阵的数据操作存在不协调，但是我没有发现具体问题出在哪。

三、MathorCup_Q2.m报错在于实现规划的语句
fun=@(x)sum(find(ar(mylist(2:end,6),x(1))>mylist(2:end,7)&ar(mylist(2:end,6),x(2))>mylist(2:end,7)&ar(mylist(2:end,6),x(3))>mylist(2:end,7)),3);
当然这条语句也是在CSDN查的。它的特点在于只能实现简单的规划。这种包含动态、集合的复杂规划如果使用这条语句，直接被MATLAB判定使用标量就被pass掉了。
如何用MATLAB，甚至LINGO实现更复杂的规划，这确实是一个问题。类似于本题规划的目标函数，庞大而可以改变。

最后附上题目来源：

【官网】2022年第十二届MathorCup高校数学建模挑战赛题

2022年4月20日凌晨于郴州