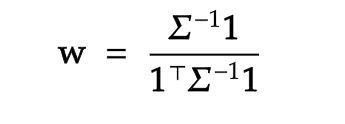合奏：机器学习中唯一（几乎）免费的午餐

弦乐合奏音源

A notebook accompanying this post can be found here.

随此帖子附带的笔记本可以在这里找到。

I am grateful to Tetyana Drobot and Igor Pozdeev for their comments and suggestions.

我感谢 Tetyana Drobot 和 Igor Pozdeev 的意见和建议。

摘要 (Summary)

In this post, I cover the somewhat overlooked topic of ensemble optimization. I begin with a brief overview of some common ensemble techniques and outline their weaknesses. I then introduce a simple ensemble optimization algorithm and demonstrate how to apply it to build ensembles of neural networks with Python and PyTorch. Towards the end of the post, I discuss the effectiveness of ensemble methods in deep learning in the context of the current literature on the loss surface geometry of neural networks.

在这篇文章中，我介绍了集成优化中一个被忽略的话题。 首先，我简要概述了一些常用的集成技术，并概述了它们的弱点。 然后，我介绍一个简单的集成优化算法，并演示如何将其应用到使用Python和PyTorch构建神经网络的集成中。 在文章的结尾，我将在神经网络的损失表面几何的最新文献的背景下，讨论集成方法在深度学习中的有效性。

Key takeaways:

关键要点:

• Strong ensembles consist of models that are both accurate and diverse
  强大的合奏包含准确且多样的模型
• There are ensemble methods that admit realistic target functions which are not suitable as direct optimization objectives for ML models (think of using cross-entropy for training while being interested in some other metric like accuracy)
  有一些集成方法可以接受现实的目标函数，这些函数不适合作为ML模型的直接优化目标(请考虑使用交叉熵进行训练，同时对准确性等其他度量标准感兴趣)
• Ensembling improves the performance of neural networks not only by dampening their inherent sensitivity to noise but also by combining qualitatively different and uncorrelated solutions
  集成不仅可以降低神经网络对噪声的固有敏感性，而且可以结合质上不同且不相关的解决方案，从而提高了神经网络的性能。

The post is organized as follows:I. IntroductionII. Ensemble OptimizationIII. Building Ensembles of Neural NetworksIV. Ensembles of Neural Networks: the Role of Loss Surface GeometryV. Conclusion

该职位的结构如下: 一，导言 二。 集成优化 III。 建立神经网络集成体 IV。 神经网络集成:损失表面几何的作用 V.结论

一，引言 (I. Introduction)

An ensemble is a collection of models designed to outperform every single one of them by combining their predictions. Strong ensembles comprise models that are accurate, performing well on their own, yet diverse in the sense of making different mistakes. This resonates with me deeply, as I am a finance professional—ensembling is akin to building a robust portfolio consisting of many individual assets and sacrificing higher expected returns on some of them in favor of an overall reduction in risk by diversifying investments. “Diversification is the only free lunch in finance” is the quote attributed to Harry Markowitz, the father of the Modern Portfolio Theory. Given that ensembling and diversification are conceptually related, and in some problems, the two are mathematically equivalent, I decided to give the post its title.

集合是一组模型，旨在通过结合它们的预测来胜过其中的每个模型。 强大的合奏包含准确的模型，可以很好地表现的模型，但是在犯不同错误的意义上却是多样的。 当我是一名金融专业人员时，这深深地引起了我的共鸣-类似于建立一个由许多个人资产组成的稳健的投资组合，并牺牲其中的一些较高的预期收益，以期通过分散投资来全面降低风险。 现代投资组合理论之父哈里·马克维兹(Harry Markowitz)的话是:“多元化是金融界唯一的免费午餐”。 考虑到集合和多样化在概念上是相关的，并且在某些问题上，两者在数学上是等效的，所以我决定给该职位起标题。

Why almost, though? Because there is always a lingering problem of computational cost given how resource hungry the most powerful models (yes, neural networks) are. In addition to that, ensembling can hurt interpretability of more transparent machine learning algorithms like decision trees by blurring the decision boundaries of individual models — this point does not really apply to neural networks for which the issue of interpretability arises already on the individual model level.

为什么差不多呢？ 鉴于资源的匮乏，最强大的模型(是的，神经网络)总是存在一个计算成本问题。 除此之外，集成还会模糊单个模型的决策边界，从而损害决策树等更透明的机器学习算法的可解释性，这一点实际上不适用于已经在单个模型级别出现可解释性问题的神经网络。

There are several approaches to building ensembles:

有几种构建合奏的方法:

• Bagging bootstraps the training set, estimates many copies of a model on the resulting samples, and then averages their predictions.

  套袋引导训练集，在所得样本上估计模型的许多副本，然后平均其预测。

• Boosting sequentially reweights the training samples forcing the model to attend to the training examples with higher loss values.

  Boosting顺序地对训练样本进行加权，迫使模型以较高的损失值参加训练样本。

• Stacking uses a separate validation set to train a meta-model that combines predictions of multiple models.

  跟踪使用单独的验证集来训练结合了多个模型预测的元模型。

See, for example, this post by Gilbert Tanner or the one by Joseph Rocca, or this post by Juhi Ramzai for an extensive overview of these methods.

见，例如， 这篇文章由吉尔伯特坦纳或在一个由约瑟夫·罗卡 ，或该职位由朱希Ramzai对这些方法的广泛概述。

Of course, the methods above come with some common problems. First, given a set of trained models how to select the ones that are most likely to generalize well? In the case of stacking, this question would read ‘how to reduce the number of ensemble candidates to a manageable amount so the stacking model can handle them without a large validation set or high risk of overfitting?’ Well, just pick the best performing models and maybe apply weights inversely proportional to their loss, right? Wrong. Though often it is a good starting point. Recall that a good ensemble consists of both accurate and diverse models: pooling several highly accurate models with strongly correlated predictions would typically result in all models stepping on the same rake.

当然，以上方法存在一些常见问题。 首先，给定一组训练有素的模型，如何选择最有可能泛化的模型？ 在堆叠的情况下，该问题将读为“如何将整体候选者的数量减少到可管理的数量，以便堆叠模型可以处理它们而无需大量的验证集或过度拟合的高风险？” 好吧，只要选择性能最好的模型，然后将权重与它们的损失成反比，对吧？ 错误。 尽管通常这是一个很好的起点。 回想一下，一个好的集合包括准确的模型和多样的模型:将具有高度相关的预测的几个高度准确的模型合并在一起通常会导致所有模型都踩着相同的耙子。

The second problem is more subtle. Often the machine learning algorithms we train are all but glorified feature extractors, i.e. the objective in a real-life application might differ significantly from the loss function used to train a model. For instance, the cross-entropy loss is a staple in classification tasks in deep learning because of its differentiability and stable numerical behavior during optimization, however, depending on the domain we might be interested in accuracy, F1 score or false negative rate. As a concrete example consider classifying extreme weather events like floods or hurricanes, where the cost of making a Type II error (false negative) could be astronomically high rendering even the accuracy let alone the cross-entropy useless as an evaluation metric. Similarly, in a regression setting, the common loss function is the mean squared error. In finance, for example, it is common to train the same model for every asset in the sample predicting the return over the next period, while in reality there are hundreds of assets in multiple portfolios with optimization objectives similar to the ones encountered in reinforcement learning and optimal control: multiple time horizons along with state and path dependencies. In any case, you are neither judged by nor compensated for low MSE (unless you are in academia).

第二个问题更加微妙。 通常，我们训练的机器学习算法只是美化了特征提取器，即，实际应用中的目标可能与训练模型所使用的损失函数有很大差异。 例如，交叉熵损失是深度学习中分类任务的主要内容，因为它的可区分性和优化过程中稳定的数值行为，但是，根据领域，我们可能对准确性，F1得分或假阴性率感兴趣。 作为一个具体示例，请考虑对洪水或飓风等极端天气事件进行分类，其中发生II型错误(假阴性)的成本在天文上可能会很高，即使是准确性，更不用说交叉熵作为评估指标了。 同样，在回归设置中，共同损失函数是均方误差。 例如，在金融领域，通常针对样本中的每种资产训练相同的模型以预测下一时期的回报，而实际上，多个投资组合中有数百种资产的优化目标与强化学习中遇到的目标相似。最佳控制:多个时间范围以及状态和路径依赖性。 无论如何，您都不会因MSE偏低而受到评判或补偿(除非您处于学术界)。

In this post I thoroughly discuss the ensemble optimization algorithm of Caruana et al. (2004) which addresses the problems outlined above. The algorithm can be broadly described as model-free greedy stacking, i.e. at every optimization step the algorithm either adds a new model to the ensemble or changes the weights of the current constituents minimizing the total loss without any overarching trainable model guiding the selection process. Equipped with several features allowing it to alleviate the overfitting problem, the Caruana et al. (2004) approach also allows building ensembles optimizing custom metrics that may differ from those used to train individual models, thus addressing the second problem. I further demonstrate how to apply the algorithm: first, to a simple example with a closed form solution and next, to a realistic problem by building an optimal ensemble of neural networks for the MNIST dataset (a complete PyTorch implementation can be found here). Towards the end of the post, I explore the mechanisms underpinning the effectiveness of ensembles in deep learning and discuss the current literature on the role of the loss surface geometry in the generalization properties of neural networks.

在这篇文章中，我彻底讨论了Caruana等人的集成优化算法。 (2004年)解决了上面概述的问题。 该算法可以广义地描述为无模型贪婪堆叠，即在每个优化步骤中，该算法要么向集合添加新模型，要么更改当前成分的权重以使总损失最小化，而无需任何总体可训练的模型来指导选择过程。 Caruana等人具有一些功能，可以减轻过拟合的问题。 (2004年)的方法还允许构建整体来优化可能不同于用于训练单个模型的自定义指标，从而解决第二个问题。 我进一步演示了如何应用该算法:首先，通过一个封闭形式的解决方案来解决一个简单的示例，其次通过为MNIST数据集构建神经网络的最佳集合来解决一个现实问题(可以在此处找到完整的PyTorch实现)。 在文章的结尾，我探索了深度学习中集成体有效性的机制，并讨论了有关损失表面几何形状在神经网络泛化特性中的作用的当前文献。

The remainder of the post is structured as follows: Section II presents the ensemble optimization approach of Caruana et al. (2004) and illustrates it with a simple numerical example. In Section III I optimize an ensemble of neural networks for the MNIST dataset (PyTorch implementation). Section IV briefly discusses the literature on the optimization landscape in deep learning and its impact on ensembling. Section V concludes.

文章的其余部分结构如下: 第二部分介绍了Caruana等人的整体优化方法。 (2004年) ，并通过一个简单的数值示例进行了说明。 在第三部分中，我为MNIST数据集( PyTorch实现 )优化了神经网络的集成。 第四部分简要讨论了深度学习中的优化前景及其对集成的影响的文献。 第五节总结。

II. Ensemble Optimization: the Caruana et al. (2004) Algorithm

二。 集成优化: Caruana等人。 (2004) 算法

The approach of Caruana et al. (2004) is rather straightforward. Given a set of trained models and their predictions on a validation set, a variant of their ensemble construction algorithm is as follows:

Caruana等人的方法。 (2004年) 非常简单。 给定一组训练有素的模型及其对验证集的预测，其集成构造算法的变体如下:

1. Set inint_size— the number of models in the initial ensemble and max_iter — the maximum number of iterations

   设置inint_size —初始集合中的模型数，以及max_iter —最大迭代数

2. Initialize the ensemble with init_size best performing models by averaging their predictions and computing the total ensemble loss

   通过对init_size最佳的模型进行平均并计算总合计损耗，使用init_size最佳的模型初始化合计

3. Add to the ensemble the model in the set (with replacement) which minimizes the total ensemble loss
   将集合中的模型添加到集合中(替换)，以最大程度减少集合损失

4. Repeat Step 3 until max_iter is reached

   重复步骤3，直到达到max_iter

This version of the algorithm includes a couple of features designed to prevent overfitting the validation set. First, initializing the ensemble with several well-performing models forms a strong initial ensemble; second, drawing models with replacement practically guarantees that the ensemble loss on the validation set does not increase as the algorithm iterations progress — if adding another model can not further improve the ensemble loss the algorithm adds copies of the incumbent models essentially adjusting their weights in the final prediction. This weight adjustment property allows thinking of the algorithm as model-free stacking. Another interesting feature of this approach is that loss functions used for ensemble construction and to train individual models are not required to be the same: as mentioned earlier, often we train models with a particular loss function because of its mathematical or computational convenience in the (reasonable) hope that the models will generalize well with a related performance metric which is hard to optimize directly. Indeed, the value of cross-entropy on the test set in a malignant tumor classification task should not be our primary concern, in contrast to, for instance, the false negative rate.

该算法的此版本包括一些旨在防止过拟合验证集的功能。 首先，用几个性能良好的模型初始化集成体，形成一个强大的初始集成体； 其次，替换模型的绘制实际上保证了验证集上的集合损失不会随着算法迭代的进行而增加-如果添加另一个模型不能进一步改善集合损失，则算法会添加现有模型的副本，从而从本质上调整它们的权重。最终预测。 此权重调整属性允许将算法视为无模型堆叠。 这种方法的另一个有趣特征是，用于整体构建和训练各个模型的损失函数不必相同:如前所述，由于(或)中的数学或计算方便性，我们经常训练具有特定损失函数的模型。合理的)，希望这些模型能够很好地推广具有难以直接优化的相关性能指标。 的确，与例如假阴性率相比，在恶性肿瘤分类任务中测试集上的交叉熵值不应成为我们的主要关注点。

The following Python function implements the algorithm:

以下Python函数实现了该算法:

Caruana et al. (2004) ensemble selection algorithm Caruana等。 (2004)整体选择算法

Consider the following toy example: assume we have 10 models with zero-mean normally distributed uncorrelated predictions. Furthermore, assume that the variance of the predictions decreases linearly from 10 to 1, i.e. the first model has the highest variance and the last model has the lowest. Given a sample of data, the goal is to build an ensemble minimizing the mean squared error against the ground truth of 0. Note, that in the context of the Caruana et al. (2004) algorithm ‘build an ensemble’ means assigning a weight between 0 and 1 to each model’s predictions such that the weighted prediction minimizes the MSE, subject to the constraint that all weights sum up to 1.

考虑以下玩具示例:假设我们有10个模型，这些模型具有零均值正态分布的不相关预测。 此外，假设预测方差从10线性减少到1，即第一个模型的方差最大，而最后一个模型的方差最低。 给定一个数据样本，目标是建立一个集合，以最小化相对于地面实数为0的均方误差。注意，在Caruana等人的上下文中。 (2004年)算法“构建整体”是指为每个模型的预测分配介于0和1之间的权重，以使加权的预测最小化MSE，但前提是所有权重之和为1。

The finance aficionados would recognize a special case of the minimum variance optimization problem by thinking of the models’ predictions as returns on some assets, and the optimization objective as minimizing portfolio variance. The problem has a closed form solution:

通过将模型的预测视为某些资产的收益，并将模型的优化目标视为最小的投资组合方差，金融爱好者将认识到最小方差优化问题的特例。 该问题有一个封闭式解决方案:

where w is the vector of model weights, and Σ is the variance-covariance matrix of predictions. In our case the predictions are uncorrelated and the off-diagonal elements of Σ are zero. The following code snippet solves this toy problem by both using the ensemble_selector function and the analytical approach, it also constructs a simple ensemble by averaging the predictions:

其中w是模型权重的向量，而Σ是预测的方差-协方差矩阵。 在我们的情况下，预测是不相关的， Σ的非对角元素为零。 以下代码段通过使用ensemble_selector函数和解析方法来解决此玩具问题，并且还通过平均预测来构造一个简单的集合:

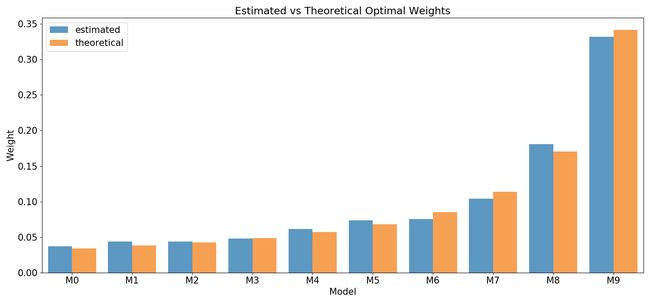
Figure 1 below compares weights implied by the ensemble optimization (in blue) and the closed form solution (in orange). The results match pretty closely, especially given that to compute the analytical solution we use the true variances and not the sample estimates. Note, that although the models with low prediction uncertainty receive higher weights, the weights of the high uncertainty models do not go to zero: the predictions are uncorrelated, and we can always reduce the variance of a weighted sum of random variables by adding an uncorrelated variable (with finite variance, of course).

下图1比较了集成优化(蓝色)和封闭式解决方案(橙色)所隐含的权重。 结果非常接近，特别是考虑到计算解析解时，我们使用的是真实方差，而不是样本估计值。 请注意，尽管预测不确定性较低的模型获得的权重较高，但不确定性较高的模型的权重不会为零:预测是不相关的，并且我们总是可以通过添加不相关性来减少随机变量加权总和的方差变量(当然具有有限方差)。

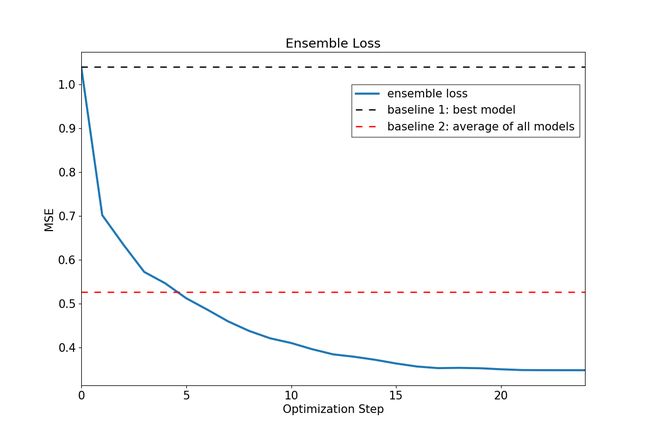
Figure 1: Estimated vs Theoretical Optimal Weights 图1:估计的最佳权重与理论上的最佳权重

The solid blue line on the next figure plots the ensemble loss for the first 25 iterations of the algorithm. The dashed black and red lines represent, respectively, the loss achieved by the best single model and by a simple ensemble that averages the predictions of all models. After approximately five iterations the optimized ensemble beats the naive one achieving significantly lower MSE values thereafter.

下图的蓝色实线表示该算法前25次迭代的总体损失。 黑色和红色虚线分别代表最佳单一模型和将所有模型的预测取平均值的简单集合所造成的损失。 经过大约五次迭代后，优化的合奏击败了幼稚的合奏，此后获得了明显更低的MSE值。

Figure 2: Ensemble Loss vs Optimization Step 图2:整体损失与优化步骤

What if the number of models in the pool is very large?

如果池中的模型数量很大怎么办？

If the model pool is very large some of the models could overfit the validation set purely by chance. Caruana et al. (2004) suggest using bagging to address this issue. In this case, the algorithm is applied to bags of M models randomly drawn from the pool with replacement with the final predictions being averaged over individual bags. For example, with a probability of 25% for a model to be drawn and 20 bags, the chance that any particular model will not be in any of the bags is only around 0.3%.

如果模型库很大，则某些模型可能纯粹是偶然地超出了验证集的范围。 Caruana等。 (2004)建议使用装袋法解决这个问题。 在这种情况下，该算法适用于从池中随机抽取并替换的M个模型袋，最终预测值将对各个袋平均。 例如，要抽取一个模型和20个袋子的概率为25％，则任何特定模型不在任何袋子中的机会仅为0.3％左右。

三， 建立神经网络集成体:MNIST示例 (III. Building Ensembles of Neural Networks: an MNIST Example)

Equipped with the techniques from the previous section, in this one, we will apply them to a realistic task, building and optimizing an ensemble of neural networks on the MNIST dataset. The results of this section can be completely replicated using the accompanying notebook, therefore I am restricting the code snippets in this section to a minimum primarily focusing on ensembling and not on model definitions and training.

在上一节中，配备了上一部分的技术，我们将把它们应用于实际任务，在MNIST数据集上建立和优化神经网络的集成。 本节的结果可以使用随附的笔记本完全复制，因此，我将本节中的代码片段限制在最低限度上，主要是集中在汇编而不是模型定义和训练上。

We start with a simple MLP having 3 hidden layers of 100 units each with ReLU activations. Naturally, the input for the MNIST datset is a 28x28 pixels image flattened into a 784-dimensional vector, and the output layer has 10 units corresponding to the number of digits. Therefore, the architecture specified by the MNISTMLP class implemented in PyTorch looks as follows:

我们从一个简单的MLP开始，该MLP具有3个100单位的隐藏层，每个隐藏层都带有ReLU激活。 自然，MNIST数据集的输入是平整为784维向量的28x28像素图像，并且输出层具有10个与位数相对应的单位。 因此，由MNISTMLP实现的MNISTMLP类指定的体系结构如下所示:

MNISTMLP(
  (layers): Sequential(
    (0): Linear(in_features=784, out_features=100, bias=True)
    (1): ReLU()
    (2): Linear(in_features=100, out_features=100, bias=True)
    (3): ReLU()
    (4): Linear(in_features=100, out_features=100, bias=True)
    (5): ReLU()
    (6): Linear(in_features=100, out_features=10, bias=True)
  )
)

We then train 10 instances of the model with independent weight initializations (i.e. everything is identical except for the starting weights) for 3 epochs each with a batch size of 32 and a learning rate of 0.001, reserving 25% of the training set of 60,000 images for validation, with the final 10,000 images comprising the test set. The objective is to minimize the cross-entropy (equivalently, negative log-likelihood). Note, that only 3 epochs of training together with a rather small capacity of each model would likely result in underfitting the data, thus allowing to demonstrate the benefits of ensembling in a more dramatic fashion.

然后，我们针对独立的权重初始化(即，除了初始权重外，其他所有权重相同)的10个模型实例训练3个时期，每个时期的批次大小为32，学习率为0.001，保留了60,000张图像的训练集中的25％用于验证，最后的10,000张图像组成测试集。 目的是最小化交叉熵(相当于负对数似然)。 请注意，只有3个时期的训练以及每个模型的较小能力可能会导致数据拟合不足，因此可以更戏剧化地展示集合的好处。

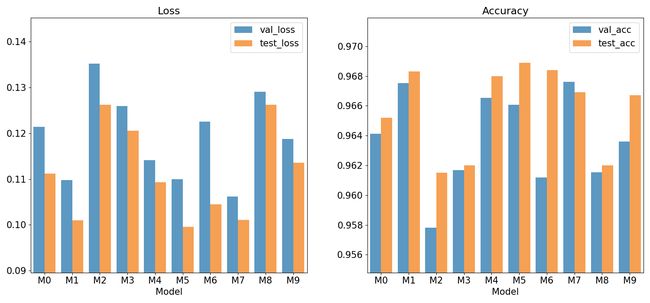
After the training is complete we restore the best checkpoints (by validation loss) of each of the 10 models. The left panel on the figure below shows the validation (in blue) and test (in orange) loss for each model named M0 through M9. Similarly, the right panel plots the validation and test accuracy.

训练完成后，我们将恢复10个模型中每个模型的最佳检查点(通过验证损失)。 下图的左面板显示了每个名为M0到M9模型的验证(蓝色)和测试(橙色)损失。 同样，右侧面板显示了验证和测试准确性。

Figure 3: Validation and Test Set Performance by Model 图3:按模型的验证和测试集性能

As expected, all models perform rather poorly with the best one, M7, achieving only 96.8% accuracy on the test set.

不出所料，所有模型的性能都相当差，最好的模型为M7 ，测试集的准确度仅为96.8％。

To build an optimal ensemble let us first call the ensemble_selector function defined in the previous section and then go over individual arguments in the context of the current problem:

为了构建最佳的集成，让我们首先调用上一节中定义的ensemble_selector函数，然后在当前问题的上下文中遍历各个参数:

y_hats_val is a dictionary with the model names as keys and predicted class probabilities for the validation set as items:

y_hats_val是一本字典，其模型名称为键，而验证集的预测类概率为项:

 >>> y_hats_val["M0"].round(3)
array([[0.   , 0.   , 0.   , ..., 0.998, 0.   , 0.001],
       [0.   , 0.003, 0.995, ..., 0.   , 0.001, 0.   ],
       [0.   , 0.   , 0.   , ..., 0.004, 0.   , 0.975],
       ...,
       [0.999, 0.   , 0.   , ..., 0.   , 0.   , 0.   ],
       [0.   , 0.   , 1.   , ..., 0.   , 0.   , 0.   ],
       [0.   , 0.   , 0.   , ..., 0.   , 0.007, 0.   ]]) >>> y_hats_val["M7"].round(3)
array([[0.   , 0.   , 0.   , ..., 1.   , 0.   , 0.   ],
       [0.   , 0.   , 1.   , ..., 0.   , 0.   , 0.   ],
       [0.   , 0.   , 0.   , ..., 0.003, 0.   , 0.981],
       ...,
       [0.997, 0.   , 0.002, ..., 0.   , 0.   , 0.   ],
       [0.   , 0.   , 1.   , ..., 0.   , 0.   , 0.   ],
       [0.   , 0.   , 0.   , ..., 0.   , 0.002, 0.   ]]) 

y_true_one_hot_val is a numpy array of the corresponding true one-hot encoded labels:

y_true_one_hot_val是对应的真正的一键编码标签的numpy数组:

 >>> 
array([[0., 0., 0., ..., 1., 0., 0.],
       [0., 0., 1., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 1.],
       ...,
       [1., 0., 0., ..., 0., 0., 0.],
       [0., 0., 1., ..., 0., 0., 0.],
       [0., 0., 0., ..., 0., 0., 0.]]) 

The loss_function is a callable mapping arrays of predictions and labels to a scalar:

loss_function是预测和标签到标量的可调用映射数组:

>>> cross_entropy(y_hats_val["M7"].round(3), y_true_one_hot_val)
0.010982255936197028

Finally, init_size=1 means that we start with an ensemble of a single model; replacement=True means that the models are not removed from the model pool after being added to the ensemble, allowing the algorithm to add the same model several times, thus adjusting the weights of the ensemble constituents; max_iter=10 sets the number of steps the algorithm takes.

最后， init_size=1意味着我们从单个模型的集合开始； replacement=True表示在将模型添加到集合后不会将其从模型池中删除，从而允许算法多次添加相同的模型，从而调整集合成分的权重； max_iter=10设置算法采取的步骤数。

Let us now examine the outputs. model_weights is a pandas dataframe containing the ensemble weight of each model for each optimization step. Dropping all models that have zero weights at each optimization step yields:

现在让我们检查输出。 model_weights是一个熊猫数据model_weights其中包含每个优化步骤每个模型的整体权重。 在每个优化步骤中删除权重为零的所有模型将得出:

>>> model_weights.loc[:, (model_weights != 0).any()]          M1        M4        M5        M7        M9
0   0.000000  0.000000  0.000000  1.000000  0.000000
1   0.000000  0.000000  0.500000  0.500000  0.000000
2   0.000000  0.000000  0.333333  0.333333  0.333333
3   0.000000  0.250000  0.250000  0.250000  0.250000
4   0.200000  0.200000  0.200000  0.200000  0.200000
5   0.166667  0.166667  0.166667  0.333333  0.166667
6   0.142857  0.142857  0.285714  0.285714  0.142857
7   0.125000  0.250000  0.250000  0.250000  0.125000
8   0.111111  0.222222  0.222222  0.222222  0.222222
9   0.100000  0.200000  0.200000  0.300000  0.200000
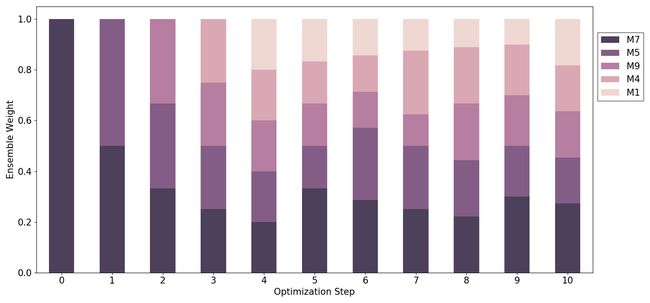
10  0.181818  0.181818  0.181818  0.272727  0.181818

The following figure plots weights of the ensemble constituents as a function of optimization steps with a darker hue corresponding to a higher average weight a model receives during all optimization steps. The ensemble initializes with a single strongest model M7 at step 0, and then progressively adds more models assigning an equal weight to each: at step 1 there are two models M7 and M5 with a 50% weight each, at step 2 the ensemble includes models M7, M5 and M9 each having a weight of one third. After step 4 no new model can further improve ensemble predictions, and the algorithm starts to adjust the weights of its constituents.

下图绘制了作为优化步骤的函数的整体成分的权重，其中较深的色相对应于模型在所有优化步骤中获得的较高的平均权重。 集成在第0步使用单个最强模型M7进行初始化，然后逐步添加更多的模型，为每个模型分配相同的权重:在第1步中，有两个模型M7和M5各自的权重为50％，在第2步中，该集成包括模型M7 ， M5和M9各自具有三分之一的重量。 在第4步之后，没有新模型可以进一步改善总体预测，并且该算法开始调整其成分的权重。

Figure 4: Ensemble Weights 图4:整体配重

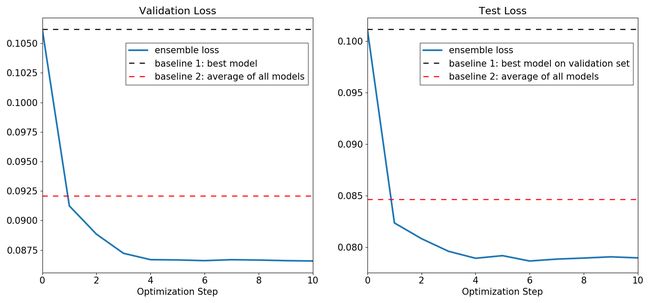
The other output — ensemble_loss — contains the loss of the ensemble at each optimization step. Similar to Figure 2 from the previous section, the left panel on the figure below plots the ensemble loss on the validation set (solid blue line) as the optimization progresses. The dashed black and red lines represent, respectively, the validation loss achieved by the best single model and by a simple ensemble which assigns equal weights to all models. The ensemble loss decreases quite rapidly, surpassing the performance of its simple counterpart after a couple of iterations and stabilizing after the algorithm enters the weight adjustment mode, which is hardly surprising given that the model pool is rather small. The right panel reports the results for the test set: at each iteration I use the current ensemble weights to produce predictions and measure loss on the test set. The ensemble generalizes well on the test sample effectively repeating the pattern observed on the validation set.

另一个输出( ensemble_loss )包含每个优化步骤的整体损失。 与上一节中的图2相似，下图的左面板在优化过程中绘制了验证集上的整体损失(蓝色实线)。 黑色和红色虚线分别代表最佳单一模型和简单的集合(将所有模型分配相等的权重)所达到的验证损失。 整体损失的下降非常快，经过两次迭代后，其性能超过了简单的整体，并且在算法进入权重调整模式后趋于稳定，鉴于模型池很小，这不足为奇。 右侧面板报告了测试集的结果:在每次迭代中，我使用当前的集成权重来生成预测并测量测试集的损失。 集合在测试样本上很好地泛化，有效地重复了在验证集上观察到的模式。

Figure 5: Ensemble Loss, MNIST 图5:MNIST的整体损失

The Caruana et al. (2004) algorithm is very flexible and we can easily adapt ensemble_selector to, for instance, directly optimize the accuracy by changing the loss_function argument:

Caruana等。 (2004)算法非常灵活，例如，我们可以通过更改loss_function参数轻松地使ensemble_selector适应于直接优化精度:

where accuracy is defined as follows:

accuracy定义如下:

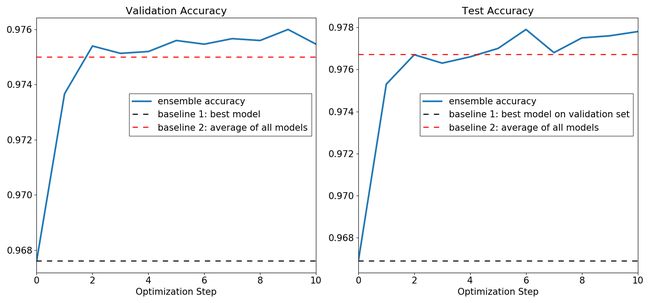
The following figure repeats the analysis in the previous one but this time for the validation and test accuracy. The conclusions are similar, although the accuracy path of the ensemble is more volatile in both samples.

下图重复了上一个的分析，但是这次是为了验证和测试准确性。 结论是相似的，尽管在两个样本中集合的准确性路径更加不稳定。

Figure 6: Ensemble Accuracy, MNIST 图6:MNIST的合奏精度

IV。 有关神经网络集成的更多信息:损失表面几何的重要性 (IV. More on Ensembling in Neural Networks: Importance of Loss Surface Geometry)

Why do random initializations work?

为什么随机初始化起作用？

The short answer — it is all about the loss surface. The current deep learning research emphasizes the importance of the optimization landscape. For instance, batch normalization (Ioffe and Szegedy (2015)) is traditionally thought to accelerate and regularize training by reducing internal covariate shift — the change in the distribution of network activations during training. However, Santurkar et al. (2018) provide a compelling argument that the success of the technique stems from another property: batch normalization makes the optimization landscape significantly smoother and thus stabilizes the gradients and speeds up training. In a similar vein, Keskar et al. (2016) argue that sharp minima on the loss surface have poor generalization properties in comparison with minima in flatter regions of the landscape.

简短的答案-全部与损失表面有关。 当前的深度学习研究强调了优化环境的重要性。 例如，传统上认为批量标准化( Ioffe和Szegedy(2015) )通过减少内部协变量漂移 (训练过程中网络激活分布的变化)来加速和规范化训练。 但是， Santurkar等。 (2018)提供了一个令人信服的论点，即该技术的成功源于另一个特性:批处理归一化使优化环境变得更加平滑，从而稳定了梯度并加快了训练速度。 同样， Keskar等人。 (2016年)认为，与景观平坦区域中的极小值相比，损失表面上的极小值极少具有泛化特性。

During training a neural network can be viewed as a function mapping parameters to loss values given the training data. The figure below plots a (very) simplified illustration of the networks’ loss landscape: the space of solutions and loss are along the horizontal and vertical axes respectively. Each point on the x-axis represents all weights and biases of the network yielding the corresponding loss (the blue solid line). The red dots show local minima where we are likely to end up using gradient-based optimization (the two leftmost dots are the global minima).

在训练期间，可以将神经网络视为将参数映射到给定训练数据的损耗值的函数。 下图绘制了网络损失状况的(非常)简化图示:解和损失的空间分别沿水平和垂直轴。 x轴上的每个点代表产生相应损失的网络的所有权重和偏差(蓝色实线)。 红点表示局部极小值，我们可能会使用基于梯度的优化来结束(最左边的两个点是全局极小值)。

In the context of ensembling, this means that we would like to explore many local minima. In the previous section we already saw that the combinations of different initializations of the same neural network architecture result in a superior generalization ability. In fact, in their recent paper Fort et al. (2019) demonstrate that random initializations end up in distant optima and therefore are capable of exploring completely different models with similar accuracy and relatively uncorrelated predictions thus forming strong ensemble components. This finding complements the standard intuition of neural networks being the ultimate low bias-high variance algorithms capable of fitting anything with almost surgical precision albeit plagued by their sensitivity to noise, and therefore benefiting from ensembling due to variance reduction.

在集合的背景下，这意味着我们想探索许多局部最小值。 在上一节中，我们已经看到，相同神经网络体系结构的不同初始化的组合产生了卓越的泛化能力。 实际上，在他们最近的论文中Fort等人。 (2019)证明了随机初始化最终会导致遥远的最优解，因此能够以相似的准确度和相对不相关的预测探索完全不同的模型，从而形成强大的整体成分。 这一发现补充了神经网络的标准直觉，后者是最终的低偏差-高方差算法，尽管由于其对噪声的敏感性而困扰，但能够以几乎外科手术的精度拟合任何事物，因此受益于因方差减少而产生的集合。

But what to do if training several copies of the same model is infeasible?

但是，如果无法训练同一模型的多个副本怎么办？

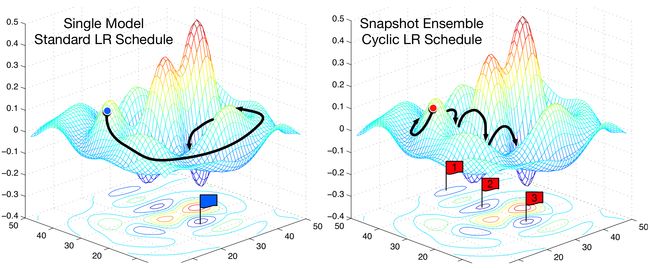
Huang et al. (2018) propose building an ensemble during a single training run using cyclical learning rate with annealing and storing a model checkpoint, or snapshot, at the end of each cycle. Intuitively, increasing the learning rate could allow the model to escape any of the local minima on the figure above and land at the neighboring region with a different local minimum eventually converging to it with a subsequent decrease in the learning rate. The next figure illustrates the snapshot ensemble technique. The left plot shows the path over the loss landscape a model traverses during the standard training regime with a constant learning rate and the final stopping point marked with a blue flag. The right plot depicts the path with a cyclical learning rate schedule and periodic snapshots marked with red flags.

黄等。 (2018)建议在单次训练中使用循环学习率和退火来构建整体，并在每个循环结束时存储模型检查点或快照。 直观地讲，提高学习率可以使模型逃脱上图中的任何局部最小值，并以不同的局部最小值降落到相邻区域，最终收敛到其上，从而降低学习率。 下图说明了快照集成技术。 左图显示了模型在标准训练过程中以恒定的学习率经过的损失景观上的路径，并以蓝色标记标记了最终的停止点。 右图描绘了带有周期性学习率计划和带有红色标记的周期性快照的路径。

Snapshot Ensembles, Source: Huang et al. (2017) 快照合奏，来源: Huang等。 (2017)

Remember, however, that on the two previous figures the whole parameter space is compressed into a single point on the x-axis and xy-plane respectively, meaning that a pair of neighboring points on the graph might be very far apart in the real parameter space, and therefore, the ability of a gradient descent algorithm to traverse multiple minima without getting stuck depends on whether the corresponding valleys on the loss surface are separated by regions of very high loss such that no meaningful increase in the learning would result in a transition to a new valley.

但是请记住，在前两个图上，整个参数空间分别被压缩为x轴和xy平面上的单个点，这意味着图形上的一对相邻点在实际参数中可能相距很远空间，因此，梯度下降算法遍历多个极小值而不会被卡住的能力取决于损耗表面上相应的波谷是否被损耗非常高的区域分隔开，从而使学习中没有有意义的增加不会导致过渡到一个新的山谷。

Fortunately, Garipov et al. (2018) demonstrate that there exist low-loss paths connecting the local minima on the optimization landscape and propose the fast geometric ensembling (FGE) procedure exploiting these connections. Izmailov et al. (2018) propose a further refinement of FGE — stochastic weight averaging (SWA).

幸运的是， 加里波夫等人。 (2018)证明在优化景观上存在连接局部极小值的低损耗路径，并提出了利用这些连接的快速几何集合(FGE)程序。 伊兹麦洛夫等。 (2018)提出了对FGE的进一步改进-随机加权平均(SWA)。

Max Pechyonkin provides an excellent overview of snapshot ensembles, FGE, and SWA.

Max Pechyonkin 很好地概述了快照合奏，FGE和SWA。

五，结论 (V. Conclusion)

Let us recap the key takeaways of this post:

让我们回顾一下这篇文章的主要内容:

• Strong ensembles consist of models that are both accurate and diverse
  强大的合奏包含准确且多样的模型

• Some model-free ensemble methods like the Caruana et al. (2004) algorithm admit realistic target functions which are not suitable as optimization objectives for ML models

  一些无模型的集成方法，例如Caruana等人。 (2004年)算法接受了不适合作为ML模型优化目标的实际目标函数

• Ensembling improves the performance of neural networks not only by dampening their inherent sensitivity to noise but also by combining qualitatively different and uncorrelated solutions
  集成不仅可以降低神经网络对噪声的固有敏感性，而且可以结合质上不同且不相关的解决方案，从而提高了神经网络的性能。

To sum up, ensemble learning techniques should arguably be among the most important tools in the arsenal of every machine learning practitioner. It is indeed quite fascinating how far the old adage of not putting all eggs in one basket goes.

综上所述，集成学习技术可以说是每位机器学习从业人员中最重要的工具之一。 确实令人着迷的是，没有把所有鸡蛋都放在一个篮子里的古老格言走了多远。

Thank you for reading. Comments and feedback are eagerly anticipated. Also, connect with me on LinkedIn.

感谢您的阅读。 迫切需要评论和反馈。 另外，在 LinkedIn 上与我联系 。

进一步阅读 (Further reading)

翻译自: https://towardsdatascience.com/ensembles-the-almost-free-lunch-in-machine-learning-91af7ebe5090

弦乐合奏音源