redis zskiplist跳表,性能堪比红黑树?(深度分析)
文章目录
- 前言
- 一、跳表原理
-
- 1、跳表?
- 2、难点在哪里?
- 3、伪代码
- 二、性能
-
- 1、跳表快在哪里?
- 2、跳表很浪费内存?
- 三、Redis实现原理
-
- 1、结构
- 2、跳表 API
- 3、基本操作
-
- 1)新增
- 2)删除
- 4、跳表的应用
- 总结
前言
本文参考源码版本为 redis6.2
跳表:
跳表(skiplist)是一种有序数据结构,它通过在每个节点中维持多个指向其他节点的指针,从而达到快速访问节点的目的。
跳跃表支持平均O(logN)、最坏O(N)复杂度的节点查找,还可以通过顺序性操作来批量处理节点。在大部分情况下,跳跃表的效率可以和平衡树相媲美,并且因为跳跃表的实现比平衡树要来得更为简单,所以有不少程序都使用跳跃表来代替平衡树。
Redis 使用跳跃表作为有序集合键的底层实现之一,如果一个有序集合包含的元素数量比较多,又或者有序集合中元素的成员(member)是比较长的字符串时,Redis 就会使用跳跃表来作为有序集合键的底层实现。
有序集合:
有序集合在生活中较常见,如根据成绩对学生进行排名、根据得分对游戏玩家进行排名等。对于有序集合的底层实现,可以使用数组、链表、平衡树等结构。数组不便于元素的插入和删除;链表的查询效率低,需要遍历所有元素;平衡树或者红黑树等结构虽然效率高但实现复杂。Redis 采用了一种新型的数据结构——跳表。跳表的效率堪比红黑树,然而其实现却远比红黑树简单。
一、跳表原理
1、跳表?
一张图带你看懂什么是跳表:
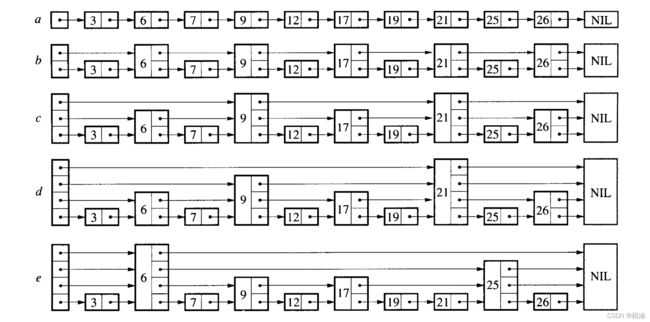
以上 a、b、c、d、e 跳表的五种形态;当然,远不止这几种情况;因为,它的结构在实现上有随机性。
什么是跳表?相信从结构上你已经看出点东西了;首先,它属于链表,因为存在指针;其次,它属于多层链表;最后,越往高层,链表节点越少,就像不同层级的索引。因此,这种链表+多级索引的结构就是跳表
你可能好奇,上下两层链表间节点个数有什么关系?哈,还真有关系!比如,你想实现上下层关系为 1 : 2、1 : 3、1 : 4 的关系,都可以满足;
注意到,1 : 2 的关系,是不是和二分法类似?当你决定使用 1 : 2 的关系时,在搜索上,它就是一个活脱脱的二分搜索,时间复杂度 O(logN)。
好,继续往下看…
一张图带你搞懂跳表的增删查改操作。是的,你没听错,一张图!
假设我们要插入元素 17:
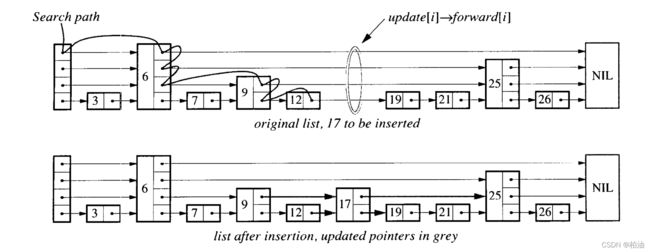
图中的曲线,就是跳表的真实搜索场景,从高层开始搜索,为啥从高层开始搜索?因为,层级越高,链表元素越少,就越容易将数据等分,类似二分搜索;如果上层搜索不到,继续往下,直到锁定元素。
增删改操作之前,都需要借助搜索操作来定位,然后在对应位置修改链表指针即可;相信你也觉得,增删改是不是非常简单?是的,跳表的思路就是非常简单。
到目前为止,跳表与Redis还没有扯上关系;也就是说,跳表,并非 Redis 所独创;跳表是一种数据结构、是一种思想,Redis 看到了它的优点,就实现它,作为 Redis 部分数据类型的底层结构。
2、难点在哪里?
上面已经讨论了,跳表对增删查改的高效型;值得注意的是,那是在元素分布比较符合预期的情况下;好,你可能疑问什么是符合预期?
上面我们提到,链表层级 (level) 提升一级,元素就会变少,并且这个比例我们可以控制;比如,这个比例用 p 表示;
假设,这里我们取 p = 1/2,也就是说,上层元素是下层的一半,如此下去,将会构成一个二分的结构;二分算法的高效查询是有目共睹的,时间复杂度 O(logN),这正是我们期望的。
因此,难点在于, 如何控制比例 p 符合预期是关键。
那么如何确定一个元素的层级?这里用了一个小技巧,当插入元素时不会去衡量列表的整体数量而强制按照比例分布元素;而是采用随机的方式决定一个新插入元素的 level,在概率上来看,大致符合比例分布。这种随机选择 level 的方式最大的好处在于处理方便高效,可以避免强制比例分布带来繁琐的元素 level 调整等开销。
既然是随机选择 level,会不会出现 level 值很大?如何控制?是有可能出现 level 很大的情况,当 level 非常大,但实际元素很小的时候,就失去了跳表的高效性;比如 level = 10000, 元素仅有 100 的情况下。因此,为避免 level 过大带来的问题,我们设定 maxLevel, 随机生成的 level 要小于等于 maxLevel。
maxLevel 取值多少合适?这取决于你列表长度能达到多少,比如 maxlevel = 32, 那么跳表节点 length = 2^32,在这个 length 范围内上下层比例大致能按照 p 分布;
level 相关伪代码如下:
randomLevel()
newLevel := 1
// random() returns a random value in [O...1)
while random() < p do
newLevel := newLevel + 1
return min(newLevel, MaxLevel)
- 1)节点层高为1的概率为 (1-p)。
- 2)节点层高为2的概率为 (1-p)p。
- 3)节点层高为3的概率为 (1-p)p^2。
- 4)……
- 5)节点层高为n的概率为 (1-p)p^(n-1)。
可以看到,level 越高,概率越小。
3、伪代码
1)搜索:
Search(list, searchKey)
x := list->header
// loop invariant: x->key < searchKey
for i := list->level downto 1 do
while x->fotward[i]< key < searchKey do
x := x->forward[i]
// x->key < searchKey <= x->forward[1]->key
x := x+forward[1]
if x->key = searchKey then return x->value
else return failure
2)插入:
Insert(list, searchKey, newvalue)
local update[1 ..MaxLevel]
x := list->header
for i := list->level downto 1 do
while x->forward[i]->key < searchKey do
x := x->forward[i]
// x->key < searchKey <= x->forward[i]->key
update[i] := x
x := x->forward[1]
if x->key = searchKey then x->value := newValue
else
newLevel := randomLevel()
if newLevel > list->level then
for i := list->level + 1 to newLevel do
update[i] := list->header
list->level := newLevel
x := makeNode(newLevel, searchKey, value)
for i := 1 to newLevel do
x->forward[i] := update[i]->forward[i]
update[i]->forward[i] := x
3)删除:
Delete(list, searchKey)
local update[1 ..MaxLevel]
x := list->header
for i := list->level downto 1 do
while x->forward[i]->key < searchKey do
x := x->forward[i]
update[i] := x
x := x->forward[1]
if x->key = searchKey then
for i := 1 to list->level do
if update[i]->forward[i] != x then break
update[i]->forward[i] := x->forward[i]
free(x)
while list->level > 1 and
list->header->forward[list->level] = NIL do
list->level := list->level - 1
关于跳跃表的基本定义和基础算法介绍,可以参考WilliamPugh关于跳跃表的论文《Skip Lists:AProbabilistic Alternative to Balanced Trees》
二、性能
1、跳表快在哪里?
从以上得知,跳表是一条链表+多级索引的结构;数据结构决定查询效率,我们来看看这种结构的查询效率
假设链表元素有 n 个,我们按照比例 p = 1/2 构建多级索引;再来看看搜索路径:

从上层往下层检索,直到检索到目标元素;由于上下层比例分布控制在 1 : 2 的关系,所以,每往下一层,元素大致被过滤掉一半。这种检索效率与二分检索一致,因此时间复杂度 O(logN)
相信你也发现了,这种链表的检索效率达到了二分检索的速度,其本质是典型的空间换时间思想。
2、跳表很浪费内存?
我们还是假设链表元素有 n 个,按照比例 p = 1/2 构建多级索引。那么这个多级索引占用空间为:
n/2 + n/4 + n/8 + ··· + 4 + 2 + 1 = n - 1
也就是多级索引占用的空间为 n - 1,相当于多占用了链表数据一倍的空间,但整体上跳表的空间复杂度为O(n)。
假设 p = 1/3 呢?
n/3 + n/9 + n/27 + ··· + 9 + 3 + 1 = (n - 1)/2
从多级索引占用的空间消耗上来看,减少了一半,但从空间复杂度上来看仍然是 O(n)。
实际上,在开发中,我们不必太在意索引占用的额外空间。因为在实际的开发中,原始链表中存储的有可能是很大的对象,而索引结点只需要存储关键值和几个指针,并不需要存储对象,所以当对象比索引结点大很多时,那索引占用的额外空间就可以忽略。
三、Redis实现原理
相信你已经理解了跳表原理,给你一个思考题:为什么 Redis 要用跳实现有序集合,而不是红黑树?
前面我们提到,跳表并非 Redis 所独创,Redis 只是实现了它,并用于自身数据类型的底层结构实现;接下来,我们来看看是如何实现并应用的。
在 redis 源码注释中作者写到:
* This skiplist implementation is almost a C translation of the original
* algorithm described by William Pugh in "Skip Lists: A Probabilistic
* Alternative to Balanced Trees", modified in three ways:
* a) this implementation allows for repeated scores.
* b) the comparison is not just by key (our 'score') but by satellite data.
* c) there is a back pointer, so it's a doubly linked list with the back
* pointers being only at "level 1". This allows to traverse the list
* from tail to head, useful for ZREVRANGE.
可以看到,redis 中的跳表实现基本就是用C从原论文中的算法翻译过来,只做了以下三点改变:
- 是允许出现重复的
scores - 这里
比较不仅是通过key(redis 中的 key 就是score),还有实际存储的数据对比 - 支持
后向指针,因此,是一个双端链表
1、结构
一个跳表中有多个节点,该节点定义为zskiplistNode,结构如下:
typedef struct zskiplistNode {
sds ele;
double score;
struct zskiplistNode *backward;
struct zskiplistLevel {
struct zskiplistNode *forward;
unsigned long span;
} level[];
} zskiplistNode;
level:层。L1 代表第一层,L2 代表第二层,… 。每个层都带有两个属性:前进指针和跨度。前进指针向后遍历,而跨度则记录了前进指针所指向节点和当前节点的距离。backward:后退指针。它指向位于当前节点的前一个节点。主要用于反向遍历。score:分值。在跳跃表中,节点按各自所保存的分值从小到大排列。ele:成员对象,各个节点存储真实数据的字段。
多个 zskiplistNode 节点串起来再通过表头串起来就构成一个跳表结构,用zskiplist表示,定义如下:
typedef struct zskiplist {
// 表头节点和表尾节点
struct zskiplistNode *header, *tail;
// 表中节点数量
unsigned long length;
// 表中层数最大的节点的层数
int level;
} zskiplist;
跳表的结构如下图所示:
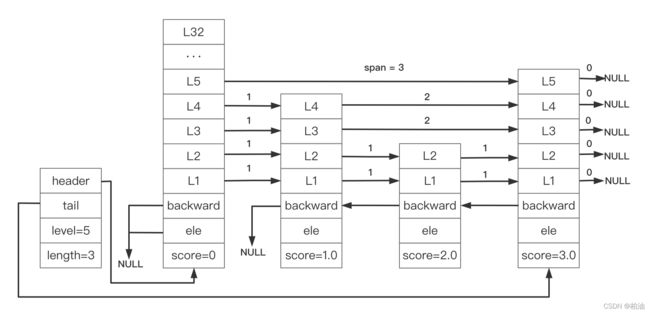
header 和 tail 指针分别指向跳跃表的表头和表尾节点,通过这两个指针,程序定位表头节点和表尾节点的复杂度为O(1)。
通过使用 length 属性来记录节点的数量,可以在O(1)复杂度内返回跳跃表的长度。
level 属性则用于在O(1)复杂度内获取跳跃表中层高最大的那个节点的层数量;当然,表头节点的层高并不计算在内。
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;x
2、跳表 API
主要的几个 API:
// 创建一个新的跳表,时间复杂度O(1)
zskiplist *zslCreate(void);
// 释放给定跳表空间以及包含的所有节点,时间复杂度O(N), N为节点个数
void zslFree(zskiplist *zsl);
// 新增节点,时间复杂度 平均 O(logN), 最坏 O(N)
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele);
// 删除节点,时间复杂度 平均 O(logN), 最坏 O(N)
int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node);
// 返回给定范围内满足条件的第一个节点,时间复杂度 平均 O(logN), 最坏 O(N)
zskiplistNode *zslFirstInRange(zskiplist *zsl, zrangespec *range);
// 返回给定范围内满足条件的最后一个节点,时间复杂度 平均 O(logN), 最坏 O(N)
zskiplistNode *zslLastInRange(zskiplist *zsl, zrangespec *range);
// 返回给定节点在跳表中的排位,时间复杂度 平均 O(logN), 最坏 O(N)
unsigned long zslGetRank(zskiplist *zsl, double score, sds o);
3、基本操作
在上面我们已经分析了论文中跳表原理,以及核心伪代码实现;在 redis 的跳表实现中也大同小异,因此,这里仅简单展示其核心实现
前面也分析过 maxLevel 作用,可以限制节点的level在指定范围内;当然,level和p的取值决定了多级链表的节点分布,最终影响的是检索的效率。
在笔者阅读的 redis6.2 源码中,maxLevel = 32, p = 1/2;这意味着,该跳表节点个数小于 2^32 之内,检索效率将近似于二分的检索效率。
好,我们继续简单往下看看,redis 源码中的一些核心实现 …
1)新增
API 定义:
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele)
插入节点的步骤:① 查找要插入的位置;② 调整跳表level;③ 插入节点;④调整backward
① 查找需要插入的位置:
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
/* store rank that is crossed to reach the insert position */
rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
rank[i] += x->level[i].span;
x = x->level[i].forward;
}
update[i] = x;
}
- update[]: 插入节点时,需要更新被插入节点每层的
forward指针。由于每层更新的节点不一样,所以将每层需要更新的节点记录在 update[i] 中。 - rank[]: 记录当前层从 header 节点到 update[i] 节点所经历的步长,在更新 update[i] 的 span 和设置新插入节点的 span 时用到。
② 调整跳表 level
// 随机生成当前节点 level
level = zslRandomLevel();
// 如果当前节点 level 大于跳表当前 zsl->level, 要尝试调整 [level, zsl->level] 之间 update[]关系,以及跳表的最高层级 zsl->level
if (level > zsl->level) {
for (i = zsl->level; i < level; i++) {
rank[i] = 0;
update[i] = zsl->header;
update[i]->level[i].span = zsl->length;
}
zsl->level = level;
}
③ 插入节点:
x = zslCreateNode(level,score,ele);
for (i = 0; i < level; i++) {
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
/* update span covered by update[i] as x is inserted here */
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
/* increment span for untouched levels */
for (i = level; i < zsl->level; i++) {
update[i]->level[i].span++;
}
简单来说,就是借助 update[] 更新各层 forward 指向以及 跨度 span。
④ 调整 backward
x->backward = (update[0] == zsl->header) ? NULL : update[0];
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
zsl->tail = x;
zsl->length++;
首先,需要理解 update[] 表示每一层待更新节点的指针;当 level = 0 时,如果 待更新节点 指向表头(zsl->header),那就将插入节点的 backward 指向 NULL,反之指向待更新节点。
同时,更新插入节点后一个节点的 backward 指向。
2)删除
① 查找删除位置:
x = zsl->header;
for (i = zsl->level-1; i >= 0; i--) {
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
x = x->level[i].forward;
}
update[i] = x;
}
这里的实现和插入节点时的查找位置一致。
② 执行删除操作:
x = x->level[0].forward;
if (x && score == x->score && sdscmp(x->ele,ele) == 0) {
zslDeleteNode(zsl, x, update);
if (!node)
zslFreeNode(x);
else
*node = x;
return 1;
}
可以看到这委托给 zslDeleteNode 执行:
③ 更新 span 和 forward:
/* Internal function used by zslDelete, zslDeleteRangeByScore and
* zslDeleteRangeByRank. */
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
int i;
for (i = 0; i < zsl->level; i++) {
if (update[i]->level[i].forward == x) {
update[i]->level[i].span += x->level[i].span - 1;
update[i]->level[i].forward = x->level[i].forward;
} else {
update[i]->level[i].span -= 1;
}
}
if (x->level[0].forward) {
x->level[0].forward->backward = x->backward;
} else {
zsl->tail = x->backward;
}
while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
zsl->level--;
zsl->length--;
}
从 redis 跳表的新增和删除实现上来看,和我们上面提到跳表相关的伪代码如出一辙,也就是说,只要搞明白了前面提到跳表相关的原理,也自然很容易的理解 redis 跳表相关实现。
鉴于此,redis 跳表相关其他 API 实现可查看源码继续阅读…
4、跳表的应用
在 Redis 中,跳跃表主要应用于有序集合的底层实现。
zset 底层使用 skiplist 条件:
zset-max-ziplist-entries: 128, 元素个数最大值。默认值为128。zset-max-ziplist-value: 64, 每个元素的字符串长度最大值。默认值为64。
即当列表元素个数大于128或者列表元素size大于64时,zset 会使用 skiplist 结构;反之会使用 ziplist 结构。
zset 添加元素的主要逻辑位于 t_zset.c 的 zaddGenericCommand 函数中。zset 插入第一个元素时,会判断下面两种条件:
- 1)zset-max-ziplist-entries 的值是否等于0;
- 2)zset-max-ziplist-value 小于要插入元素的字符串长度。
满足任一条件 Redis 就会采用跳表作为底层实现,否则采用压缩列表作为底层实现方式。
if (server.zset_max_ziplist_entries == 0 ||
server.zset_max_ziplist_value < sdslen(c->argv[scoreidx+1]->ptr))
{
zobj = createZsetObject();
} else {
zobj = createZsetZiplistObject();
}
当然,在 zset 使用中的 skiplist 和 ziplist 结构也存在互相转换:
void zsetConvertToZiplistIfNeeded(robj *zobj, size_t maxelelen) {
if (zobj->encoding == OBJ_ENCODING_ZIPLIST) return;
zset *zset = zobj->ptr;
if (zset->zsl->length <= server.zset_max_ziplist_entries &&
maxelelen <= server.zset_max_ziplist_value)
zsetConvert(zobj,OBJ_ENCODING_ZIPLIST);
}
if (zzlLength(zobj->ptr) > server.zset_max_ziplist_entries ||
sdslen(ele) > server.zset_max_ziplist_value)
zsetConvert(zobj,OBJ_ENCODING_SKIPLIST);
Redis 中跳表的另一个用途是在集群节点中用作内部数据结构,除此之外,跳表在 Redis 里面没有其他用途。
总结
跳表的原理简单,其查询、插入、删除的平均复杂度都为O(logN)。跳表主要应用于有序集合的底层实现。其特点如下:
-
跳表是
有序集合的底层实现之一。 -
Redis 的跳表实现由
zskiplist和zskiplistNode两个结构组成,其中 zskiplist 用于保存跳表信息(比如表头节点、表尾节点、长度),而 zskiplistNode 则用于表示跳表节点。 -
每个跳跃表节点的层高都是1至32之间的随机数。
-
在同一个跳跃表中,多个节点可以包含相同的分值,但每个节点的成员对象必须是唯一的。
-
跳跃表中的节点按照分值大小进行排序,当分值相同时,节点按照成员对象的大小进行排序。
为什么 Redis 要用跳表来实现有序集合,而不是红黑树?
Redis 中的有序集合支持的核心操作主要有下面这几个:
- 插入一个数据;
- 删除一个数据;
- 查找一个数据;
- 按照区间查找数据;
- 迭代输出有序序列。
其中,插入、删除、查找以及迭代输出有序序列这几个操作,红黑树也可以完成,时间复杂度跟跳表是一样的。但是,按照区间来查找数据这个操作,红黑树的效率没有跳表高。
对于按照区间查找数据这个操作,跳表可以做到 O(logn) 的时间复杂度定位区间的起点,然后在原始链表中顺序往后遍历就可以了。这样做非常高效。
当然,Redis 之所以用跳表来实现有序集合,还有其他原因,比如,跳表更容易代码实现。虽然跳表的实现也不简单,但比起红黑树来说还是好懂、好写多了,而简单就意味着可读性好,不容易出错。还有,跳表更加灵活,它可以通过改变索引构建策略,有效平衡执行效率和内存消耗。
不过,跳表也不能完全替代红黑树。因为红黑树比跳表的出现要早一些,很多编程语言中的 Map 类型都是通过红黑树来实现的。我们做业务开发的时候,直接拿来用就可以了,不用费劲自己去实现一个红黑树,但是跳表并没有一个现成的实现,所以在开发中,如果你想使用跳表,必须要自己实现。
参考:
《Skip Lists:AProbabilistic Alternative to Balanced Trees》