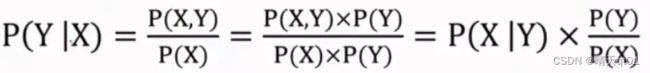【机器学习算法】朴素贝叶斯算法,该算法有非常好的特性,在big data的情况下,它支持数据更新和数据逐渐更改。
-
- 朴素贝叶斯(naïve bayes):
之前我们已经把文本处理的内容讲完了,
现在开始进入机器学习算法的内容。
朴素贝叶斯的原理是贝式定理
能解决什么问题
案例。
它一般之适用于分类问题,线性回归一般只能用于数字预测问题。
这个图要逆着看。我们整理一下思路
我们可以看右下角的表格,这个就是我们这次给的数据,可以发现第一个字段是数字字段年龄,第二个字段是收入,是否为学生,信用程度。
来判断是否会购买电脑。
这里举了一个案例:当年龄小于等于30,收入是medium,学生是yes,信用是fair
那么我们进行概率的预测。我们可以看第1行,的概率,就是在X为基础下购买电脑的可能性
第2行就是在x的基础是不购买电脑的概率。
1,2行如果除以P(x)的话,那他们的和就是1,以为我们其实最后就是比大小,所以不除也问题不大
3,4行是题目里购买电脑和不购买电脑的频率,这个就可以直接带来12
接下来我们要得到X分别在购买电脑和不购买电脑的频率率,先得到年龄小于等于30的2个频率,收入为midium的2个频率,以此类推,得到8个概率。
独立假设:
因为我们假设他们是相互独立的,所以总概率就是4个字段的乘积。进行一个联乘(把购买电脑的情况下的4个字段联乘)
我们可以发现这个模型的基础挺简单。
为什么明明是bayes模型,我们缺要给他添加一个词朴素呢(naïve,有天真的意思)
这是因为我们做了一个简单的假设
独立性假设
因为我们把联合概率,也就是4个字段的概率相乘,就直接看作条件概率。说明我们进行的了一个假设:认为字段之间相互独立,互不影响。
概率的归一化
我们结果是必须进行一个归一化,不然不符合现实逻辑,也就是不买电脑的概率加上买电脑的概率等于1.也就是说要除以P(x)
因为和必须是1,所以我们认为P(x等于0.035=0.028+0.007)
那么买电脑的概率就是0.028/0.035,百分之80
不买电脑的概率就是0.007/0.035,百分之20
这样朴素贝叶斯模型才算完美。
拉普拉斯转化
但是我们还能对概率进行更符合现实逻辑的处理,也就是拉普拉斯转化。就例如买电脑这件事,可能我们求出来的概率为0,但是没有什么东西概率是完全为0的。应该有一点概率(有可能其中一个字段的概率为0)
我们就可以利用拉普拉斯转化进行修正。(其实很简单,就是对每一类都加很小的一个概率,比如0.001)
做朴素贝叶斯算法的几个关键点:
就这个案例,提出一些关于假设的问题:比如年龄与收入,是无关的吗,当然不是,一般年龄越高收入就越高。学生和收入,一般也是有关系的,不可能相互独立,做独立性假设其实就是为了让计算变的简单。但是一般都不能达到假设条件,就实际而言,怎么做的效果其实都不错。
于是就有学者去探讨,为什么明明假设是错误的,但是结果却一般都很好用呢?
有人就归纳2个原因。
原因1:我们对分类问题中的每个都进行了假设,所以每个分类中都出现了错误,那么错误就得到了抵消
原因2:因为我们需要的不是一个非常准确的数值,而是只需要对的概率值,大于错的概率值。
所以独立性假设,其实很多情况下都不是有很大影响。(但也导致了它只适合分类问题。)
还有一件事:朴素贝叶斯其实是贝式网络的简化,后者其实是神经网络的一种。参数量很大,所以要大量的数据,反而会不如朴素贝叶斯模型。后面会用说其中的一个子模型(参数量很大)
还有一件事:朴素贝叶斯其实隐藏了一个假设,它认为每个字段都一样重要。因为我们算每个条件都是直接联乘,没有进行权重的处理。逻辑回归,多元回归都会进行不同的权重。
还有一件事:朴素贝叶斯不会进行字段或者特征的选择,所以做朴素贝叶斯的时候,一定要进行字段的筛选。
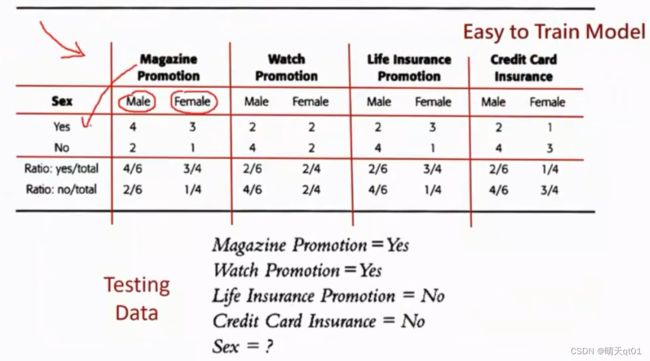
案例:判断性别
判断性别的重要性。比如图书馆,市场,都会进行一些商品的推荐,性别对喜爱商品的影响其实是挺大的,所以我们要尽量了解性别特征。所以社群网络就要进行预测。
字段1是杂志促销。字段2是手表促销。字段3是人寿保险促销,字段4是信用卡保险促销。这是记录。
这里我们就希望了解男生女生对这个活动是不是有不同的倾向。
于是我们就可以用朴素贝叶斯做判断。
下面这个表格其实就是朴素贝叶斯模型。对应了各自情况下的概率。
训练朴素贝叶斯模型也非常容易,只要把数据从第一个读到最后一个就可以了。
然后就可以保留这个表,引入我们测试的4个条件。计算概率值:
我们取出对应的概率,进行乘积就可以了。得到结果,0.0593
是女性的结果为0.0281
显然0.0594大于0.0281
所以认为测试集是男性
记得,朴素贝叶斯是预测分类的问题。计算方法就是,在a条件下的b,就要求在b条件下的a概率乘以a的概率,除以b的概率。
一般前者是多个字段概率连乘积。。
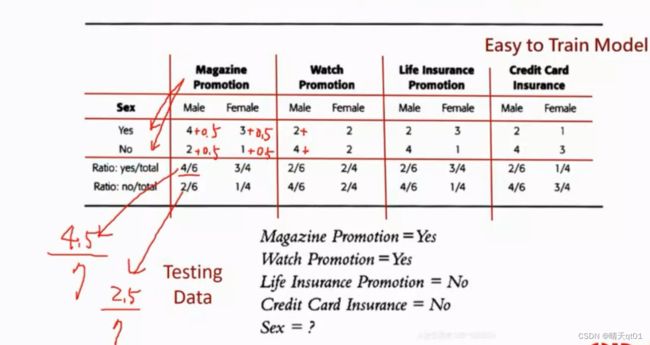
如果其中一个字段概率是0:因为只要其中一个字段是0,因为我们求字段概率是连乘,那么朴素贝叶斯的求和结果就一定是0,无论其他数字有多大。
处理方法也很简单,就是和我们之前运用的拉普拉斯方法相似。我们给每个字段不同的情况下概率值都增加一个小的数值。
这就是空值的处理方法,因为我们这个案例没有一个是0的情况,但是其实0的情况经常出现的。
处理方法如下。
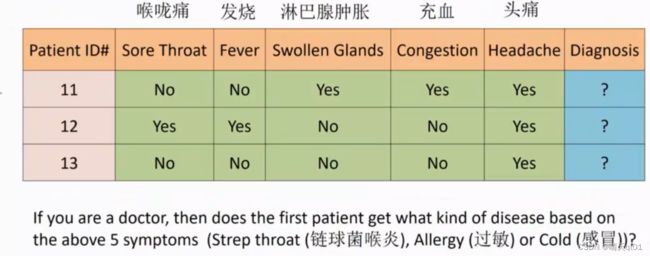
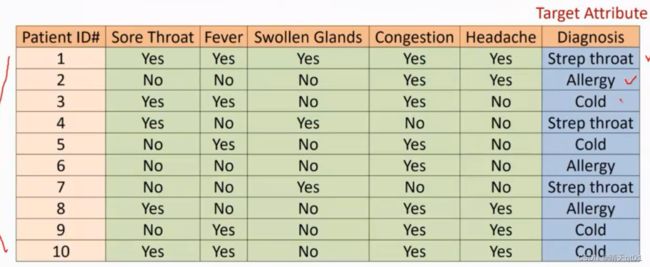
案例2:多分类的bayes模型。
这里有3个数据,我们希望通过朴素bayes的模型得到这3个案例的疾病所在。
有5个字段,分别对应不同的症状。
我们的测试集是
那么我们这么继续bayes继续病症预测呢?
同样,我们要得到,在了解这5个症状的条件下得3种疾病的3种概率。
公式就是
然后我们就计算各自的概率就可以
这里就不细说了,大家应该都会了。
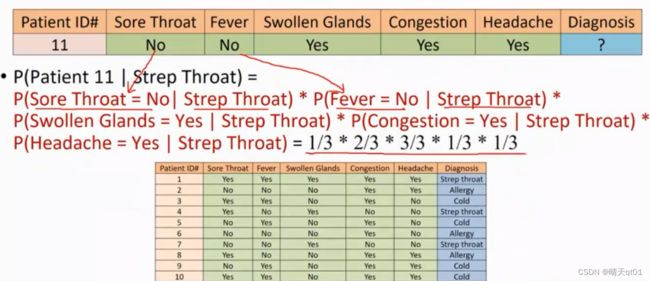
我们计算第11个患者情况的时候结果如下
因为我们没有处理为0的概率,所以就会出现百分百得病概率的情况。。
空值的问题
最后说明一下空值的问题,比如第二个手表促销的问题,我们就可以直接忽略掉该字段。我们传统的朴素贝叶斯就不用进行空值填补,朴素贝叶斯它会直接当做没看见。
朴素贝叶斯对数值型的处理
虽然贝叶斯视乎只能进行类别型计算,但是数值型字段可以进行处理,方法有两种,数值离散化,正态分布处理方法。
把正态分布进行数值型字段的处理方式。
正态分布预测概率方法,如果对数值型,
案例:我们添加一个年龄字段。
这是只要有平均值和标准差,就可以。
分别求男生和女生的平均值和标准差。然后我们直接用正态分布的公式去代入求概率。
如图所示。
45岁是红色线。我们可以发现,是女生的概率比较大。
朴素贝叶斯有非常好的特性,的big data的情况下,它支持数据更新和数据逐渐学习。而决策树等等模型都得重新建模。
这个算法简单且效果好。
贝式网络的子模型,TAN
一个字段除了和目标字段有关之外,最多只能和一个输入字段有关,这里我们就把它的前提规则进行了放宽。但是它需要更多的参数,如果我们的数据量不够大,就会出现更糟的结果。
-
-
- 不同类型的朴素贝叶斯
-
由于python软件对贝叶斯建立的时候,不接受类别型字段的输入,因此,衍生出3种朴素贝叶斯模型的建立方法。
类型1:针对数值型特征的朴素贝叶斯
将所有的类别型字段进行独热模型的处理(比如现在有3类,我们就要编码为100,010,001),把它变为二元的Dummy字段。所有字段的值可以视作正态分布的方式呈现
然后以sklearn.naive_bayes.GaussianNB(高斯分布)做概率的估计
类型2: 针对类别型及顺序型特征的朴素贝叶斯模型
将数值型字段离散化为类别型字段,在将它变为二元的Dummy字段
然后以sklearn.naive_bayes.BernoulliNB(伯努利分布)做概率的估计
类型3:针对二元类别型特征的朴素贝叶斯模型
在文本分析中,每个关键词出现在每篇文章的次数,并非以正态的分布的形式呈现。
然后以sklearn.naive_bayes.multinomialNB(多项式分布)做概率的估计
可能会疑问,为什么我们要用分布的方式去计算概率,而不是用之前的数值去计算概率
主要原因就是因为当数据集数量太小的时候,那么从资料集中计算出来的概率值,偏差将十分严重。
举例来说,我们观察一个质地均匀的骰子,投掷6次的结果是【1,3,1,5,3,3】,如果我们按照这六次的概率去计算每个点的概率,和真实的概率相差将会非常大。
通过概率分布来计算概率,就可以解决这个问题。