现代计算机图形学入门(四)———— 着色
文章目录
- 1 可见性(Visibility)
-
- 1.1 画家算法
- 1.2 Z-Buffer算法
- 2 着色(Shading)
-
- 2.1 Blinn-Phong反射模型
-
- 2.1.1 漫反射(Diffuse)
- 2.1.2 高光(Specular)
- 2.2.3 环境光照(Ambient)
- 2.2 着色频率(Shading Frequencies)
- 2.3 渲染管线(Graphics Pipline)
- 3 纹理映射(Texture Mapping)
-
- 3.1 重心坐标(Barycentric Coordinates)
- 3.2 纹理太小
- 3.3 纹理太大
- 3.4 纹理应用
-
- 3.4.1 环境映射(Environment Mapping)
- 3.4.2 凹凸贴图/法线贴图(Bump Mapping)
- 3.4.3 位移贴图(Displacement Mapping)
- 3.4.4 三维纹理
- 3.4.5 记录算好的信息
- 3.4.6 体渲染(Volume rendering)
1 可见性(Visibility)
1.1 画家算法
对于一幅图,我们一般是先把远景画完,然后再用近景将部分远景覆盖,最终得到一幅画,在图形学中这样的一种算法过程被称为画家算法

在图形学中我们想画一个立方体,画画的顺序也挺讲究,如下正方体,如果我们不是以左上右下的顺序画,左面就会有一条棱线显现出来。
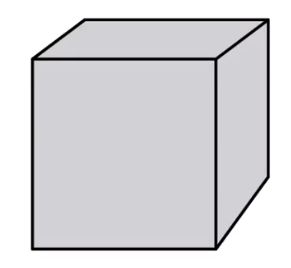
在一般的情况下,我们利用画家算法,对要画的n个三角形排下序O(logn),然后再着色,也可以对大部分的情景有效。但是对于这样的场景,画家算法就无法排序了,为了解决这个问题,引入了Z-Buffer算法。

1.2 Z-Buffer算法
由于对空间中每个三角形不好排序,因此Z-Buffer算法选择对空间中的每个像素进行排序,我们会记录每个三角形内各个像素的最浅深度,因此我们设置了两个缓存,一个用来存储每个像素值叫做frame buffer,一个用来存储每个像素的深度叫做depth buffer,渲染结果和深度图会同步更新。为了简化计算,我们认为Z表示摄像机离图形的距离,Z越大表示越远,越小表示越近,这与之前定义的Z不一样。对于n个三角形,Z-Buffer算法来着色三角形的时间复杂度为O(n)。Z-Buffer算法应用于MSAA,则是对每个采样点进行深度缓存计算而不是每个像素。


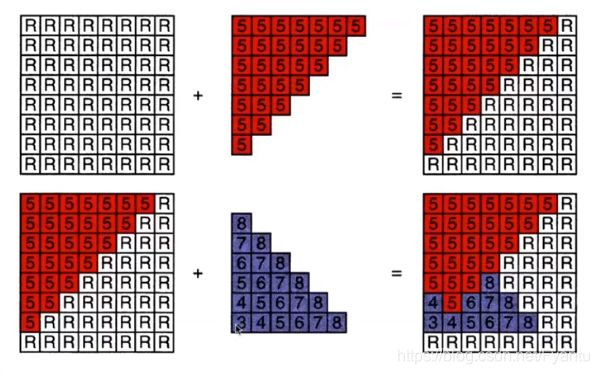
Z-Buffer算法相较于画家算法有一个好处,就是结果与更新像素的顺序是没有关系的,不管是哪种顺序最后都可以得到最终的图像。不过在实际中,由于我们存储的深度值都是浮点型的数字,而在计算机中我们判断两个浮点数是否相等实际上很难判断,因此有这个好处的前提是更新前后的深度值没有相同的情况下。同时还要注意,Z-Buffer处理不了透明物体,透明物体的处理需要特殊处理。
2 着色(Shading)
2.1 Blinn-Phong反射模型
对于这样一幅有光照的图片,我们可以看到着色分为三个部分,分别是高光、漫反射和环境光照

对于某个反射点,我们定义了如下输入参数:
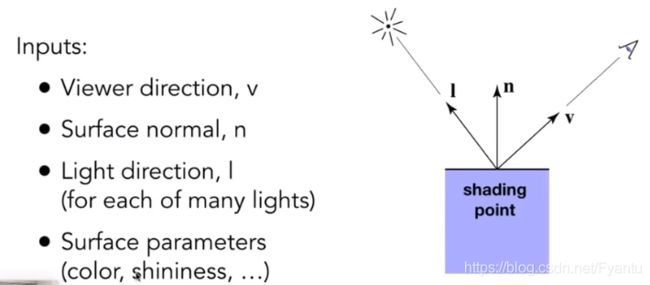
要注意的是,着色(Shading)是针对物体本身的,是不考虑其它物体的存在,因此不会产生阴影。如图就只有物体上方出现了光晕,而物体右下方却没有阴影。

2.1.1 漫反射(Diffuse)
当光线打到某一点后,光线会均匀的反射到各个方向去就叫漫反射
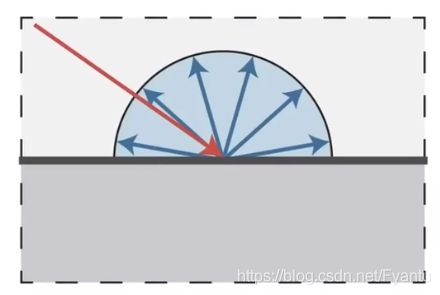
不过不同的光,以不同的角度照射上去会导致明暗不一样,通过观测我们可以找到一个结论,就是某个反射点接受到的光照多少由它的夹角决定,当夹角越大,被光射到的有效面积就越小,因此体现的就要越暗。
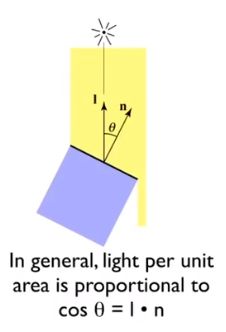
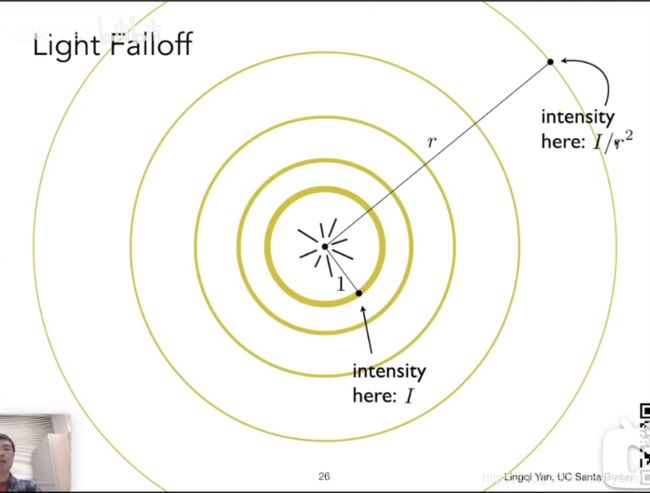
对于发射光,我们假定光是向四面八方传播的,在每一个时刻光线都聚焦在某一个球面上,我们假定距离为1时光线强度为I,且光在传播过程能量是守恒的。
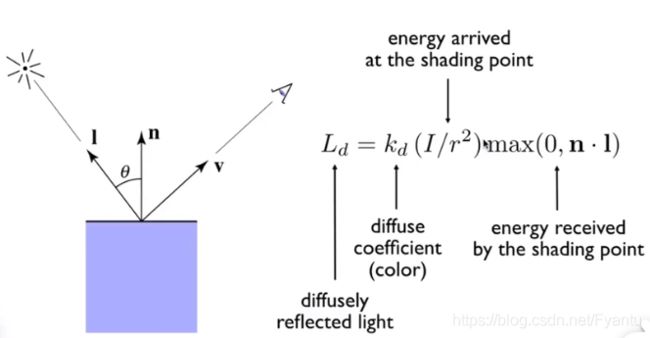
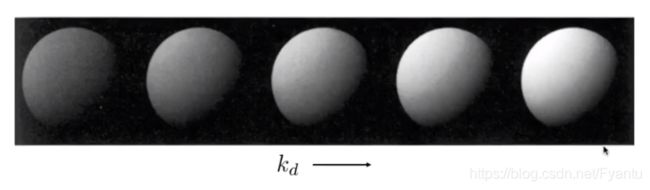
因此结合释放的能量和接受的能量,我们可以得出点光源到达某一反射点时的能量,其中Max函数中带了一个0的原因是,有的时候余弦角算出来是负数的,也就是从下方射入反射点,这个时候就取0,kd为漫反射系数,表示的材料吸收能量的能力,它其实也代表了材料的颜色,会影响材料整体的明亮程度。我们可以发现在式子中并没有提到v,这是因为漫反射是向四面八方反射的,因此反而不需要考虑。
2.1.2 高光(Specular)
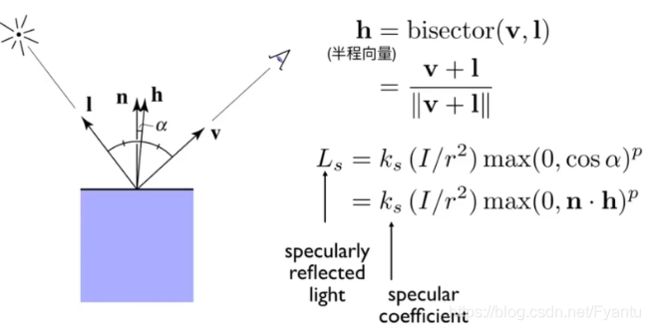
如果反射面足够光滑,那么我们入射角和出射角是一样的,如果是比较光滑,那么反射光会在出射角方向的一定角度范围内发散,也就是观察方向与镜面反射方向接近的时候会看到高光。
在Blinn-Phong模型中,由于目光所看到的方向不好算,因此我们求出入射光与目光方向的角平分线方向,也就是半程向量h,半程向量h方向与法线n方向接近,就反应了v和R接近(观察方向与镜面反射方向接近),这样是否有高光只要看半程向量与法线是否接近。通常认为ks(镜面反射系数)为一个白的颜色。由于Blinn-Phong是一个经验模型,因此他简化了光的能量传播,因此未将n与l相乘。
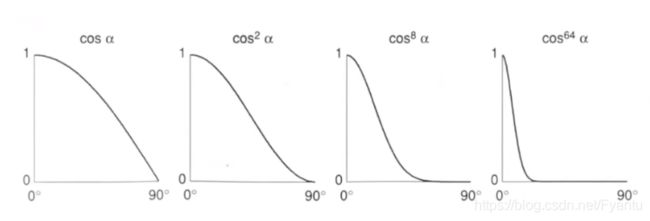
由于余弦对应的角在90度内都会有高光,这样会导致图形上很大一片区域都是高光,因此需要加上一个指数,让图像上部分区域是高光,这样就只有一些角度反射的会形成高光,其他角度则不会,看起来也更自然。

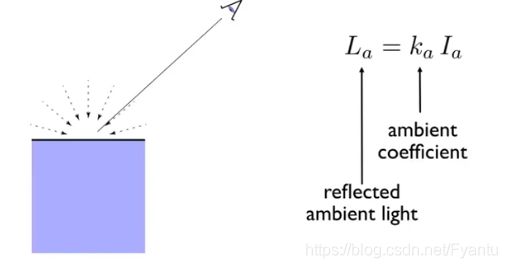
2.2.3 环境光照(Ambient)
环境光照不讲究从哪个地方进来,他与实际的直接的光照没啥关系,也就是与L方向没啥关系,并且无论从哪看都是一样的,和V也没关系,所以环境光就是一个常数,也就是一个颜色。所以环境光的目的是为了保证没有地方是黑的,它只是把所有其他的光叠加起来提升一个亮度。我们假设图形上某一个点来自环境的光强在任何时候是相同的为Ia,乘上环境光系数Ka,即为环境光。
将三种光照加起来,就是Blinn-Phong模型

2.2 着色频率(Shading Frequencies)
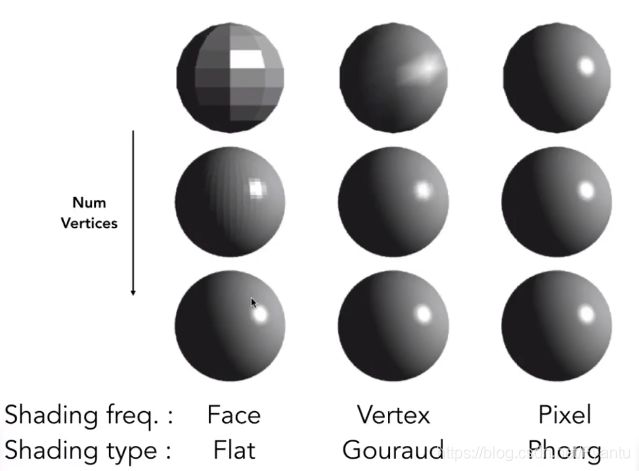
不同的着色频率会产生不同的高光特效,可以分为对三角形着色、对顶点着色和对像素着色三种。
![]()
把每个三角形当做一个平面,通过叉积将每个三角形的法线求出来,然后通过计算得到整个三角形的shading结果,这样的方式叫 Flat shading

如果把每个三角形的每个顶点的法线求出来,从而求出每个三角形顶点的shading,三角形内部的shading则通过插值的方法算出来,这样的方式叫Gouraud shading。

由于每个顶点是与周围的面相连接,因此顶点的法线可以通过将该顶点周围面法线求平均来得出,注意这个平均是加权平均,因为更大的面对法线方向的影响更大。

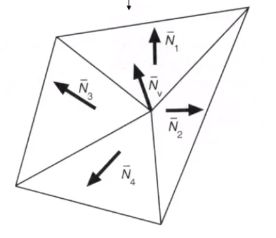
对每个像素求法线方向从而得出每个像素的颜色,这样的方式就叫Phong shading,不过也是开销最大的。

假如已经知道三角形顶点的法线,那么内部逐像素的法线求解需要用到重心坐标
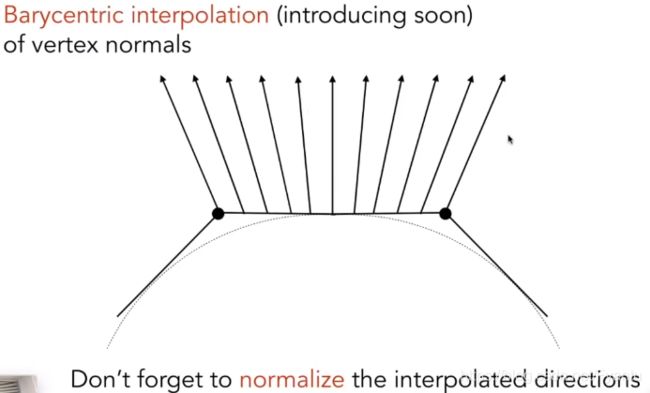
不过着色频率取决于点面等出现的频率,当每个三角形面足够小的时候,那就不也不需要很复杂的逐像素的着色频率了,当他的模型图像小于一个像素时,Phong shading的计算量反而比Flat shading要小,因此哪种频率更好取决于实际情况,不能单纯的说Phong shading比Flat shading要好。
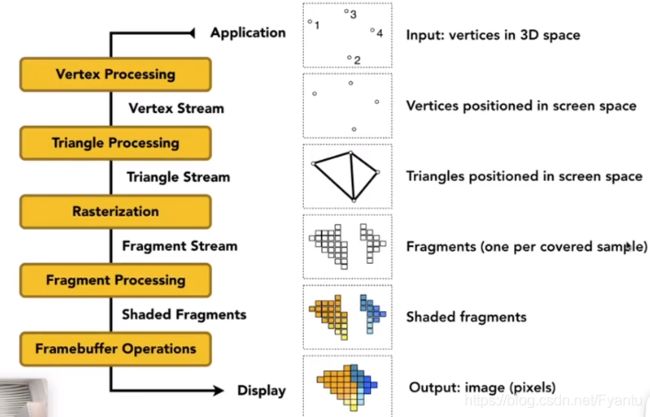
2.3 渲染管线(Graphics Pipline)
将之前所学的合起来,即为渲染管线。首先是输入三维空间中的点,将这些点投影到屏幕上,将屏幕上的点连接形成三角形,再通过光栅化离散成为在不同像素上的表示,然后对每个像素进行着色,最后可以得到整个屏幕上的图形。整个操作就是在硬件显卡中显示图像完成的操作,开发商一般提供了接口可以来编程顶点、像素等如何着色,一般将定义顶点、像素如何着色的这段代码成为shader。
3 纹理映射(Texture Mapping)
我们希望对一个图形,他不同的点可以有不同的属性,例如在着色的时候,我们通过纹理来希望不同的点可以有不同的颜色。在图形学中,纹理就是一张图,这张图可以通过拉伸、压缩等罩在三维物体的表面,这个过程就叫做纹理映射。
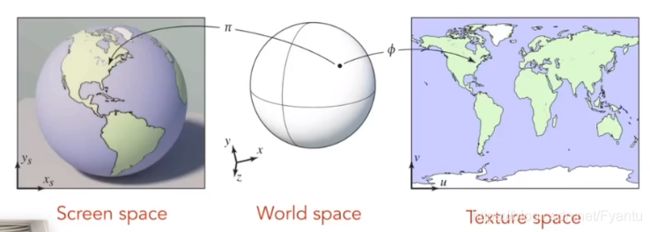
图形学中我们将每个图形扣成了由2D的图形组成的面,我们希望每个小图形在纹理前后都是无缝衔接的,这就需要我们让原图形与纹理上的图形的坐标要一一对应。

纹理上的坐标系是以(u,v)来表示,不管纹理的范围是多少,一般u和v的大小都在(0,1)内,三角形上任意一个顶点都对应一个(u,v)
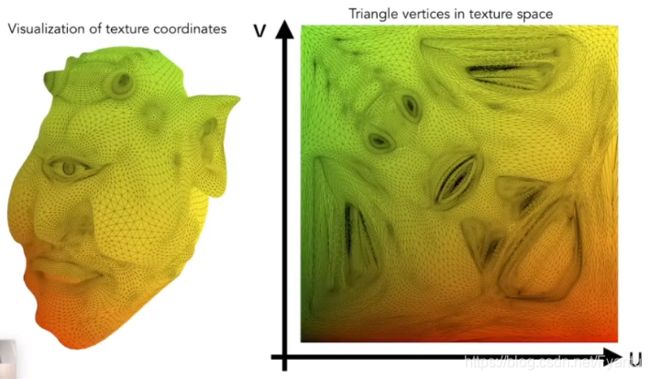
图片上三角形的每一个点都可以在纹理上找到对应的颜色,但不是一 一对应的关系,可以图形上多个区域对应同一个纹理,纹理本身设计好,使得其往四周复制的时候可以无缝衔接,这样的纹理被称为tiled texture


3.1 重心坐标(Barycentric Coordinates)
我们已知了三角形内部顶点的值,现在希望可以通过插值的方法来平滑的得到三角形内部每个点的值,并且由于三角形顶点有很多属性,例如颜色、法线等,因此插值基本对三角形内的任意属性都要进行,因此我们引入了重心坐标。
重心坐标的定义是针对每一个三角形的,三角形平面内的任意一点的坐标都可以用顶点坐标的线性组合来表示,只要其加和为1,那么就在平面上,如果坐标没有负数,那么就表示该点在三角形内。
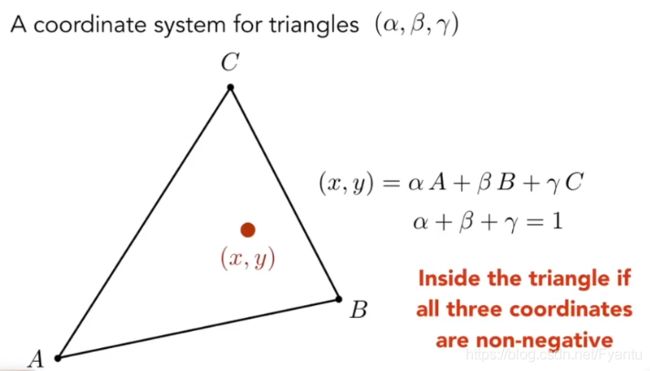
α、β 和 γ 如何求可以通过面积比来得到
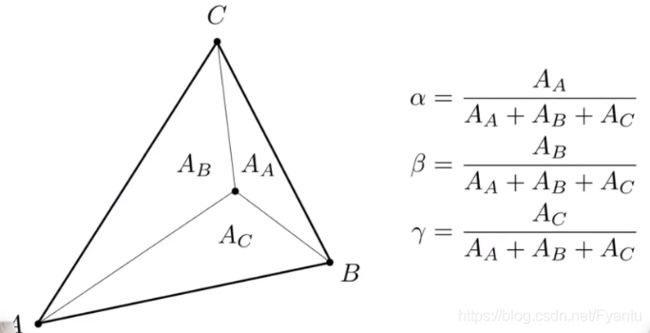
也有一种简化方法是这样:
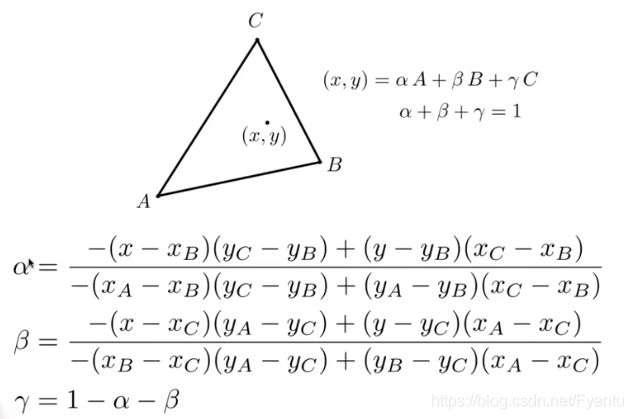
三角形内点的坐标可以通过重心坐标得到,同理,三角形内点的属性也可以通过重心坐标来得到:
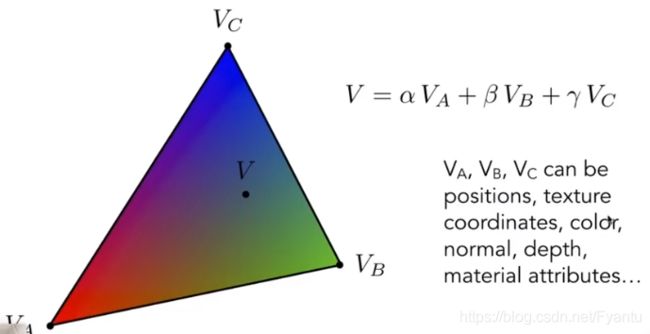
但是要记住,重心坐标在投影下是会变化的,投影前的重心坐标在投影后使用会有误差。因此要插值一些三维空间中的属性,就需要取顶点在三维空间中的坐标,然后求出三维空间中的重心坐标再做插值,再把值投影到二维空间上去,而不能在投影之后的三角形做插值。
因此可以通过三角形的顶点坐标,利用重心坐标来得到里面每个像素的坐标,然后通过坐标来查询对应纹理的颜色,再利用纹理上图的颜色来代替对应的漫反射系数Kd。

3.2 纹理太小
假如一个纹理的分辨率是 256 x 256,而我们要看的图像是4K级别的,那么每个纹理就会被拉大,所以得到的纹理坐标就会是一个非整数的坐标,这就是纹理太小导致的。采取四舍五入的方式,那么会有多个图形中的像素(pixel)对应到同一个纹理元素(texel),这就会导致图像上像素不是连续的,出现好多格子

为了使图形放大后的颜色看起来比较平滑,而不是离散的状态从而产生很多的格子,我们使用双线性插值(Bilinear interpolation)来求图形像素内每个位置上的颜色,双线性插值求水平和竖直的顺序对结果没有影响。

当然也有更精确的,例如Bicubic插值取周围的16个进行插值,并且每4个进行一个三次的插值而不是线性的。
3.3 纹理太大
当纹理太大时则会产生摩尔纹,这是因为近处的像素只覆盖一部分纹理,但是远处的像素覆盖了很大一块纹理,这样像素上取的点只是纹理上很大一片区域的平均值,这明显是不正确的。这样就会产生走样问题,近处的点可能产生锯齿,而远处的点产生摩尔纹。

纹理过大从采样的角度来说,是因为我们的取样点不够,一个像素内包含了很多的纹理,频率很高,但我们只用了一个采样点去采样显然是不够的。可以采用超采样的方式,一个像素内取很多的点进行采样,但这样太耗费资源了。那如果我们不进行采样,我们只要知道我们屏幕上每个像素所对应的平均值是多少,就可以避免这个问题了,这其实就是属于点查询问题(求像素内任意一点的纹理)和范围查询问题(求一片纹理的平均值)。
由于我们的图像在不同地方覆盖的纹理有所不同,因此我们这个范围查询应该是可以覆盖大小的,因此引入了Mipmap算法,它速度很快,但只能得到近似的正方形的查询,它通过不断地把图像的分辨率缩小一半来得到最终的结果。

相比于原本只需要存储一张照片的存储量,使用Mipmap存储我们使用的存储量是原来的4/3倍(1+1/4+16/1+…(2^log n)/1),也就是额外存储的照片量总和只有原来的1/3。
那么范围查询中的范围应该如何确定呢,针对像素内的每个采样点,我们选取四周与其相近的两个采样点,然后求出该点与其相邻点映射到纹理上有多长的距离,取最长距离为近似边长所得到的正方形即为纹理范围。(公式为微分形式是指像素一个距离对应纹理多少距离)
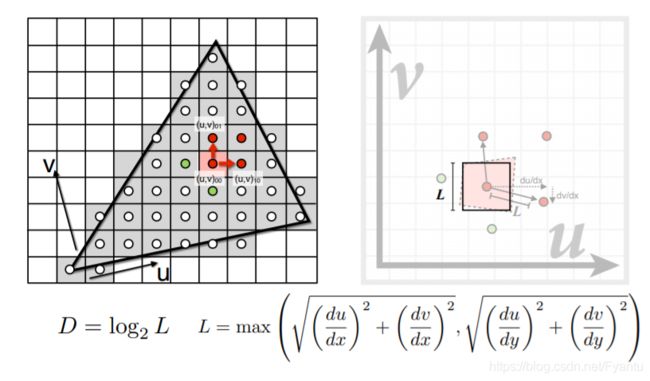
由于这个区域是一个正方形区域,那么我们距离为L的正方形只要找到层数为log2 L的层的Mipmap,即为它所要找的像素值,例如区域大小为 4 x 4,那么在第二层就会变成 1 x 1,既可以找到对应的像素值。但这样有一个问题就是由于查询的层数是离散的,因此可能导致图像上会出现很多的缝显得不自然。

因此我们在第 D 层和第 D+1 层进行双线性插值得到结果,再将两层的结果进行一个线性插值就可以得到连续层的值,这种方式也叫 三线性插值(Trilinear Interpolation),通过三线性插值我们可以只做一次查询就得到覆盖区域所得到的值,他只需要两次查询和一次插值即可得到任意连续层任意一个位置的值。
但是Mipmap会把远处所有的细节全部忽略掉(Overblur),这是因为它是针对正方形的区域,因此引入了比三线性插值效果更好的各向异性过滤(Anisotropic Filtering),它相比于Mipmap还多计算了不同长宽比的预计算(Mipmap只计算对角线上图形),这样可以得到一些压扁了的区域(矩形区域)而非只有正方形区域,不过他的总开销也变为原来的3倍,但各向异性过滤对于斜着的图形效果仍然不太好。

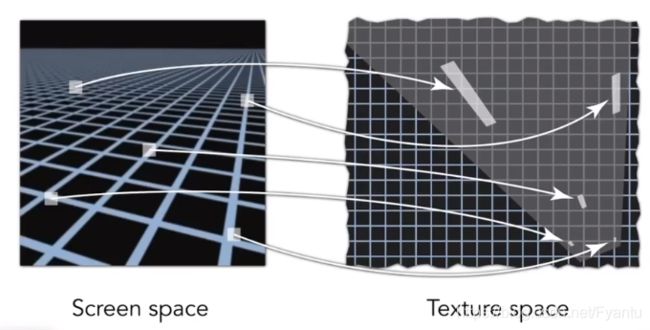
各向异性指的是在不同的方向表现不同,在游戏中显示为 3x 即为计算竖直/水平被压缩3次后的所有图形,随着压缩倍数的提高,最后总存储量会趋于原来存储的3倍,因此各向异性过滤只是对显存有要求,对于计算力并无关系。
因此引入EWA过滤(EWA filtering),它使用很多的圆形来覆盖不规则区域,通过多次查询来覆盖对应区域,但也因此生成更多的开销。

3.4 纹理应用
3.4.1 环境映射(Environment Mapping)
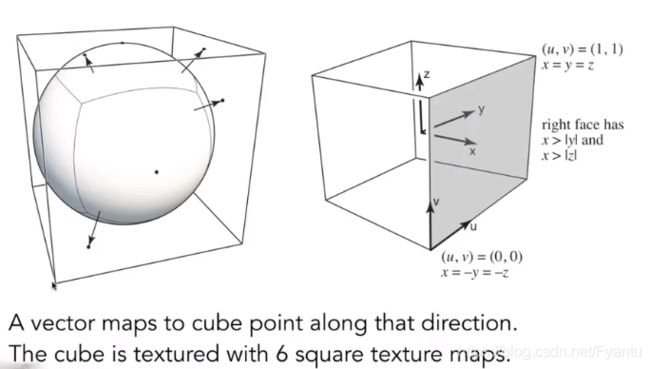
在现代GPU中,我们可以把纹理理解成是一块内存,我们可以对这块区域进行点查询,范围查询,可以滤波等等,因此没必要把纹理限制成一个图像,此我们可以直接用纹理来表示环境光照。不过用纹理来描述环境光的时候假设了我们只记录它的方向信息,也就是假设了光源是无限远。

不过如果我们把环境光记录在球上(Spherical map),会导致一个问题——扭曲,就类似地球展开来看会发现南北极比较小,因为纬度越高的地方扭曲的就越厉害。

为了解决这个问题,我们将球用一个包围盒包住,假设光照打到球上后反射到对应立方体上, 也就是将光源信息存在立方体上而不是球上,这种方法叫做 Cube map
3.4.2 凹凸贴图/法线贴图(Bump Mapping)
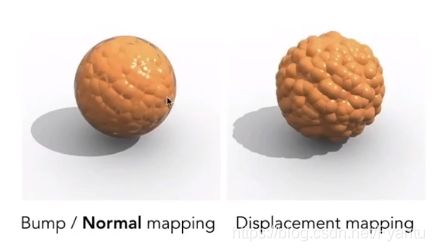
我们可以在不改变几何形体的情况下,通过改变纹理来改变几何形体不同位置的相对高度,从而产生不同的法线方向,从而造成不同的shadering,着色的明暗对比就会让人认为有凹凸的东西。

由于法线贴图只是改变纹理而不是几何形状,因此组成它的三角形数目不变。然后使用凹凸贴图对任意一个像素的法线进行扰动,通过不同位置的高度以及与邻近位置的高度差来重新定义法线,所以其实纹理记录的是任意一个点它相对位置的移动。
我们先假设原法线向量是垂直向上的,法线和u,v可以构成一个坐标系,取点(0,0,1),利用差分方法求出u和v方向上的切线,然后对切线逆时针旋转90度再标准化,就可以求出对应的法线。由于在实际世界中我们不可能所有的法线都是竖直方向的,因此我们再通过一个坐标变化将法线方向转换为实际世界中的方向。

3.4.3 位移贴图(Displacement Mapping)
由于凹凸贴图没有改变几何的形状,因此在边缘部分,以及几何体投影到自己身上的情况时会有缺陷,而位移贴图改变了每个三角形的不同顶点的位置,但位移贴图也有缺陷,它需要顶点足够细,因为它改变的是三角形顶点的位置,如果三角形不是足够细的的话,那么三角形内部需要发生变化就跟不上了,也就是三角形的变化频率跟得上纹理的变化频率。
为了可以达到最逼真的效果,我们可以尝试先用大三角形粗糙的进行位移贴图,在贴图的过程检测三角形是否需要变得更小更细,如果需要再把三角形拆成更多更小的三角形,这就是动态曲面细分(Dynamic Tessellation),这个功能在Direct X中的得到了使用。
3.4.4 三维纹理
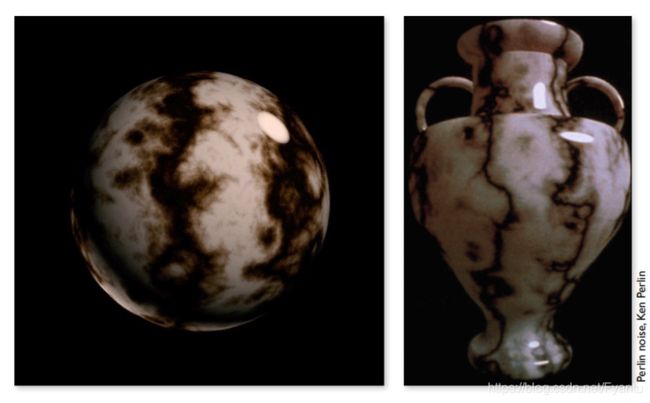
可以定义三维空间中任意一个点的值来当做3维纹理,通过定义三维空间中的噪声函数,我们可以算出每个点的值,将这个噪声函数进行一系列处理就可以得到我们想要的纹理,著名的噪声函数有Perlin noise。
3.4.5 记录算好的信息
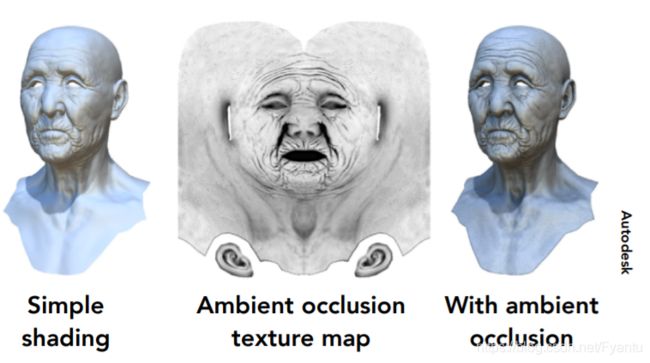
例如我们之前已经做好了着色(shading),但还不知道如何做阴影,例如下面的眉毛部分有一块骨头会遮挡住眼睛产生阴影,如果我们在shading的时候要把这块信息算好是非常费事的,但也可以算,可以通过**环境光遮蔽(Ambient occlusion)**来得到。但我们也可以把这些计算好了之后写进纹理中,后面用的时候再贴上。将着色结果乘以计算好的环境光遮蔽,就可以快速得到结果。
3.4.6 体渲染(Volume rendering)
原本的光照模型只是考虑一个表面,而事实上在医学核磁共振中,经常返回的是三维空间上的信息例如密度,这些信息可以拿过来进行渲染得到一个结果,这些信息及存储在空间中,又可以当做一个纹理进行存储。