数学建模:插值与拟合—拟合问题的python求解
目录
-
- 1.polyfit 进行多项式拟合
- 2.curve_fit
Python 的多个模块中,有很多函数或方法可以拟合未知参数。例如 NumPy 库中的多项式拟合函数 polyfit;scipy.optimize 模块中的函数 leastsq,curve_fit 都可以进行拟合。本文介绍 polyfit 和 curve_fit 的使用方法。
1.polyfit 进行多项式拟合
numpy.polyfit 的基本用法为
import numpy as np
p=np.polyfit(x, y, n) #拟合n次多项式, x,y是待拟合数据
yhat=np.polyval(p,x0) #预测, x0是待预测的点, 可以是多个值的列表
例1 对表中的数据进行二次多项式拟合。并求 x = 0.25 , 0.35 x=0.25, 0.35 x=0.25,0.35 时, y y y 的预测值。
| x i x_i xi | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| y i y_i yi | -0.447 | 1.978 | 3.28 | 6.16 | 7.08 | 7.34 | 7.66 | 9.56 | 9.48 | 9.30 | 11.2 |
求解的Python程序为
import numpy as np
import matplotlib.pyplot as plt
x0=np.arange(0, 1.1, 0.1)
y0=np.array([-0.447, 1.978, 3.28, 6.16, 7.08, 7.34, 7.66, 9.56, 9.48, 9.30, 11.2])
p=np.polyfit(x0, y0, 2) #拟合多项式 (2次)
print("拟合二次多项式的从高次幂到低次幂系数分别为:",p)
yhat=np.polyval(p,[0.25, 0.35]) #预测
print("预测值分别为:", yhat)
plt.rc('font',size=16)
plt.plot(x0, y0, '*', x0, np.polyval(p, x0), '-')
plt.show()
运行结果为
拟合二次多项式的从高次幂到低次幂系数分别为: [-9.81083916 20.12929371 -0.03167133]
预测值分别为: [4.38747465 5.81175367]
所以拟合的二次多项式为 y = − 9.8108 x 2 + 20.1293 x − 0.0317 y = - 9.8108{x^2} + 20.1293x - 0.0317 y=−9.8108x2+20.1293x−0.0317 ; x = 0.25 , 0.35 x = 0.25,\;0.35 x=0.25,0.35 时, y y y 的预测值分别为 4.3875, 5.8118。
2.curve_fit
scipy.optimize.curve_fit 的调用格式为:
from scipy.optimize import curve_fit
popt, pcov = curve_fit(func, xdata, ydata)
其中 func 是拟合的函数,xdata 是自变量的观测值,ydata 是函数的观测值,返回值 popt 是拟合的参数,pcov 是参数的协方差矩阵。
续例1 用 curve_fit 函数拟合二次多项式,并求预测值。
求解的 Python 程序为
import numpy as np
from scipy.optimize import curve_fit
y=lambda x, a, b, c: a*x**2+b*x+c #定义拟合函数
x0=np.arange(0, 1.1, 0.1)
y0=np.array([-0.447, 1.978, 3.28, 6.16, 7.08, 7.34, 7.66, 9.56, 9.48, 9.30, 11.2])
popt, pcov=curve_fit(y, x0, y0) #用curve_fit函数拟合
print("拟合的参数值为:", popt)
print("预测值分别为:", y(np.array([0.25, 0.35]), *popt))
运行结果为
拟合二次多项式的从高次幂到低次幂系数分别为: [-9.81083916 20.12929371 -0.03167133]
预测值分别为: [4.38747465 5.81175367]
所以拟合的二次多项式为 y = − 9.8108 x 2 + 20.1293 x − 0.0317 y = - 9.8108{x^2} + 20.1293x - 0.0317 y=−9.8108x2+20.1293x−0.0317 ; x = 0.25 , 0.35 x = 0.25,\;0.35 x=0.25,0.35 时, y y y 的预测值分别为 4.3875, 5.8118。
例2 用表中 x 1 , x 2 , y {x_1},{x_2},y x1,x2,y 的观测值拟合函数 z = a e b x + c y 2 z = a{e^{bx}} + c{y^2} z=aebx+cy2 。
| x x x | 6 | 2 | 6 | 7 | 4 | 2 | 5 | 9 |
|---|---|---|---|---|---|---|---|---|
| y y y | 4 | 9 | 5 | 3 | 8 | 5 | 8 | 2 |
| z z z | 5 | 2 | 1 | 9 | 7 | 4 | 3 | 3 |
求解的 Python 程序如下
import numpy as np
from scipy.optimize import curve_fit
x0=np.array([6, 2, 6, 7, 4, 2, 5, 9])
y0=np.array([4, 9, 5, 3, 8, 5, 8, 2])
z0=np.array([5, 2, 1, 9, 7, 4, 3, 3])
xy0=np.vstack((x0, y0)) # np.vstack() 按垂直方向(行顺序)堆叠数组构成一个新的数组
# # np.hstack() 按水平方向(列顺序)堆叠数组构成一个新的数组
def Pfun(t, a, b, c):
return a*np.exp(b*t[0])+c*t[1]**2 #定义拟合函数
popt, pcov=curve_fit(Pfun, xy0, z0)
print("a, b, c的拟合值为: ", popt)
运行结果为
a, b, c的拟合值为: [ 5.08907305e+00 -2.58248004e-03 -2.14509683e-02]
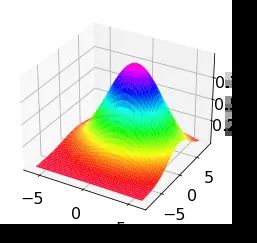
例3 利用模拟数据拟合曲面 z = e − ( x − μ 1 ) 2 + ( y − μ 2 ) 2 2 σ 2 , z = {e^{ - \;\frac{{{{(x - {\mu _1})}^2} + {{(y - {\mu _2})}^2}}}{{2{\sigma ^2}}}}}, z=e−2σ2(x−μ1)2+(y−μ2)2, 并画出拟合曲面的图形。
我们利用函数 z = e − ( x − μ 1 ) 2 + ( y − μ 2 ) 2 2 σ 2 , z = {e^{ - \;\frac{{{{(x - {\mu _1})}^2} + {{(y - {\mu _2})}^2}}}{{2{\sigma ^2}}}}}, z=e−2σ2(x−μ1)2+(y−μ2)2, 其中 μ 1 = 1 {\mu _1} = 1 μ1=1 , μ 2 = 2 {\mu _2} = 2 μ2=2 , σ = 3 \sigma = 3 σ=3 ,生成加噪声的模拟数据,利用模拟数据拟合参数 μ 1 {\mu _1} μ1, ${\mu _2}, σ \sigma σ ,最后画出拟合曲面的图形。
Python 程序如下
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
m=200; n=300
x=np.linspace(-6, 6, m)
y=np.linspace(-8, 8, n)
x2, y2 = np.meshgrid(x, y) # np.meshgrid() 生成网格点坐标矩阵
x3=np.reshape(x2, (1,-1))
y3=np.reshape(y2, (1,-1))
xy=np.vstack((x3,y3))
def Pfun(t, m1, m2, s):
return np.exp(-((t[0]-m1)**2+(t[1]-m2)**2)/(2*s**2)) #定义函数
z=Pfun(xy, 1, 2, 3)
zr=z+0.2*np.random.normal(size=z.shape) #噪声数据
popt, pcov=curve_fit(Pfun, xy, zr) #拟合参数
print("三个参数的拟合值分别为:",popt)
zn=Pfun(xy, *popt) #计算拟合值/预测
zn2=np.reshape(zn, x2.shape)
plt.rc('font',size=16)
ax=plt.axes(projection='3d') #创建一个三维坐标轴对象
ax.plot_surface(x2, y2, zn2,cmap='gist_rainbow')
plt.show()
运行结果为
三个参数的拟合值分别为: [0.99986549 2.00183698 2.99883453]