卷积与反卷积,池化与反池化
这里写目录标题
- 1. 说明
- 卷积
- 反卷积
- 池化
- 反池化
- **小证明:**
1. 说明
上采样有3种常见的方法:双线性插值(bilinear),反卷积(Transposed Convolution),反池化(Unpooling)
这里指的反卷积,也叫转置卷积,它并不是正向卷积的完全逆过程,用一句话来解释:反卷积是一种特殊的正向卷积,先按照一定的比例通过补 0来扩大输入图像的尺寸,接着旋转卷积核,再进行正向卷积。
。
https://blog.csdn.net/qq_27871973/article/details/82973048
上采样:指的是任何可以让图像变成更高分辨率的技术。最简单的方式是重采样和插值:将输入图片进行rescale到一个想要的尺寸,而且计算每个点的像素点,使用如双线性插值等插值方法对其余点进行插值来完成上采样过程。
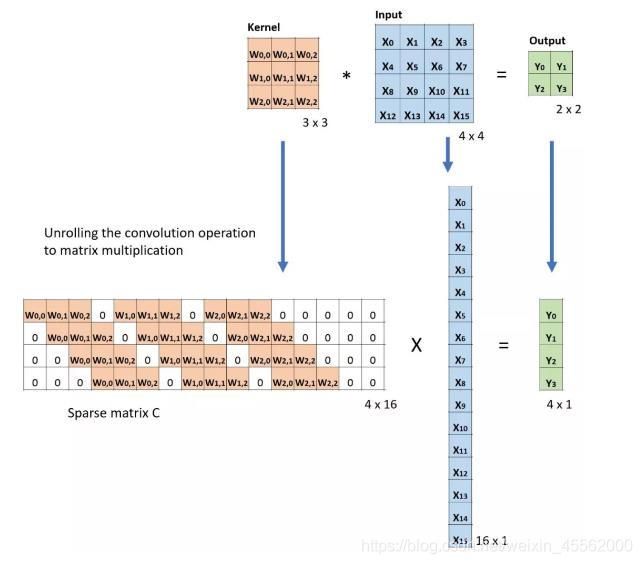
卷积
https://blog.csdn.net/quiet_girl/article/details/84579038
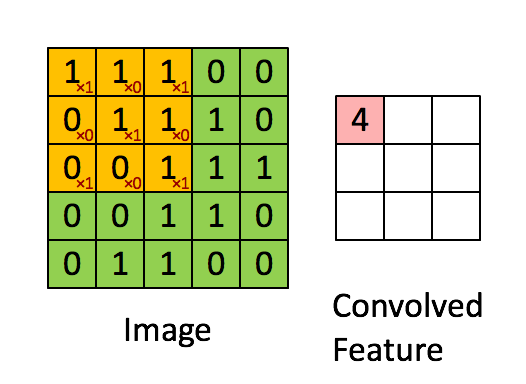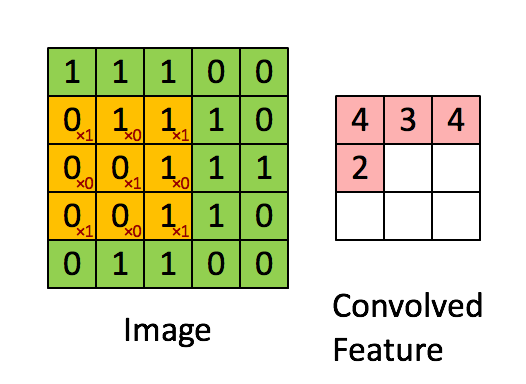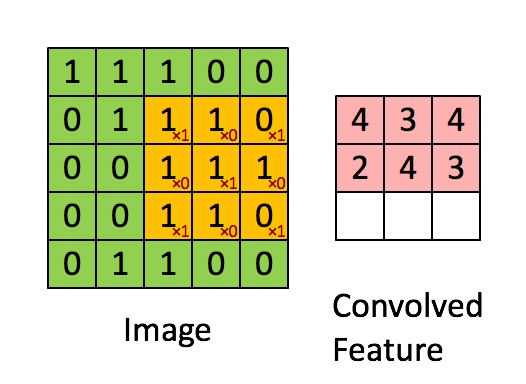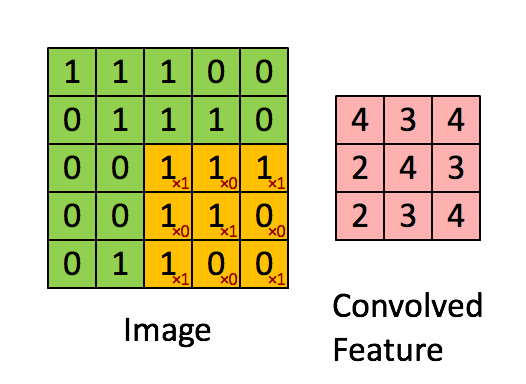
首先形象理解,就是别卷积的各元素乘以卷积核的对应元素相加
如: 1 ∗ 1 + 1 ∗ 0 + 1 ∗ 1 + 0 ∗ 0 + 1 ∗ 1 + 1 ∗ 0 + 0 ∗ 1 + 1 ∗ 0 + 1 ∗ 1 = 4 1*1+1*0+1*1+0*0+1*1+1*0+0*1+1*0+1*1=4 1∗1+1∗0+1∗1+0∗0+1∗1+1∗0+0∗1+1∗0+1∗1=4
反卷积
https://blog.csdn.net/quiet_girl/article/details/84579038
https://www.jiqizhixin.com/articles/2019-02-28-3
反卷积是指,通过测量输出和已知输入重构未知输入的过程。在神经网络中,反卷积过程并不具备学习的能力,仅仅是用于可视化一个已经 训练好的卷积网络模型,没有学习训练的过程。
在神经网络的研究中,反卷积更多的是充当 可视化的作用。对于一个复杂的深度卷积网络, 通过每层若干个卷积核的变换,我们无法知道每 个卷积核关注的是什么,变换后的特征是什么样 子。通过反卷积的还原,可以对这些问题有个清 晰的可视化,以各层得到的特征图作为输入,进 行反卷积,得到反卷积结果,用以验证显示各层 提取到的特征图。
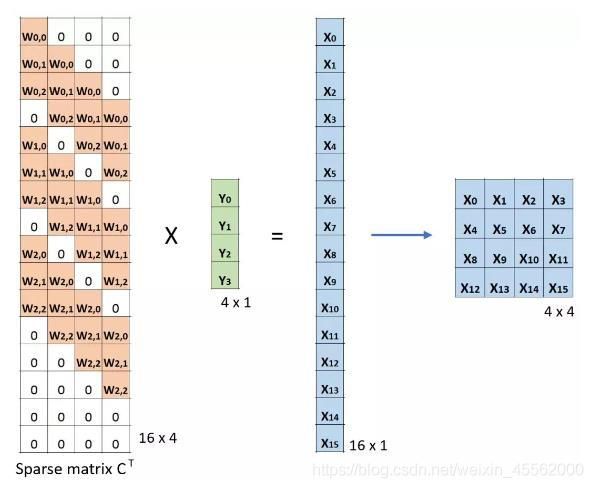
反卷积,可以理解为卷积操作的逆操作。这 里千万不要当成反卷积操作可以复原卷积操作的 输入值,反卷积并没有那个功能,它仅仅是将卷 积变换过程中的步骤反向变换一次而已,通过将卷积核转置(原理图卷积核的转置),与卷积后的结果再做一遍卷积,所以它还有个名字叫是转置卷积。
虽然它不能还原出原来卷积的样子,但是在 作用上具有类似的效果,可以将带有小部分缺失的信息最大化地恢复,也可以用来恢复被卷积生成后的原始输入。
操作:
(1)首先是将卷积核反转(并不是转置, 而是上下左右方向进行递序操作)。
(2)再将卷积结果作为输入,做补0的扩充 操作,即往每一个元素后面补0。这一步是根据步 长来的,对每一个元素沿着步长的方向补(步 长-1)个0。例如,步长为1就不用补0了。
(3)在扩充后的输入基础上再对整体补0。 以原始输入的shape作为输出,按照前面介绍的卷 积padding规则,计算pading的补0位置及个数,(倒推)得 到的补0位置要上下和左右各自颠倒一下。
(4)将补0后的卷积结果作为真正的输入,反转后的卷积核为filter,进行步长为1的卷积操 作
计算padding按规则补0时,统一 按照padding=‘SAME’,步长为1×1的方式来计 算
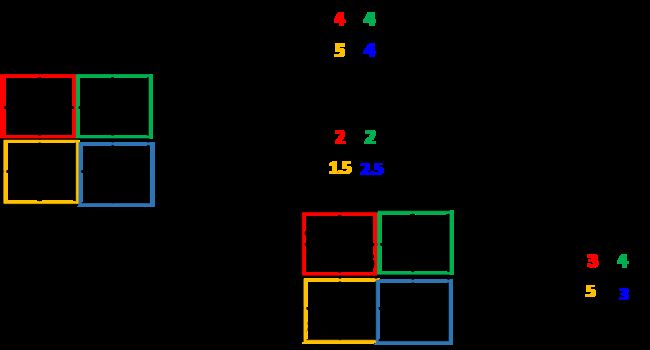
以一个4*4的矩阵 为例,进行filter为2×2,步长为2×2的卷积操作 (a所示),其对应的反卷积操作步骤如 图b所示。
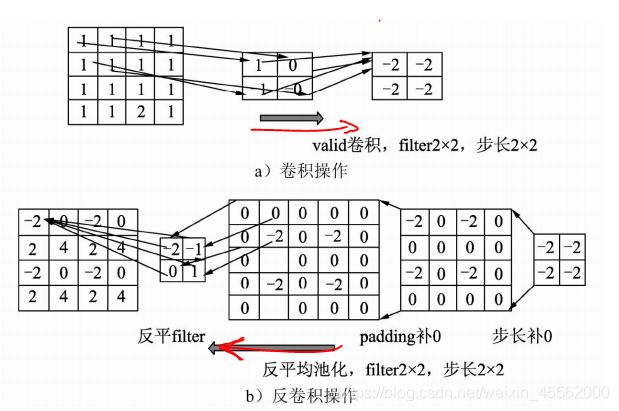
在反卷积过程中,首先将2×2矩阵通过步长 补0的方式变成4×4,再通过padding反方向补0, 然后与反转后的filter使用步长为1×1的卷积操 作,最终得出了结果。但是这个结果已经与原来 的全1矩阵不等了,说明转置卷积只能恢复部分特 征,无法百分百地恢复原始数据。
池化
最大池化是对局部的值取最大;平均池化是对局部的值取平均;随机池化是根据概率对局部的值进行采样,采样结果便是池化结果。概念非常容易理解,其示意图如下所示:
反池化
池化有两种最大池化和平均池化,其反池化也需要与其对应。
平均池化的操作比较简单。首先还原成原 来的大小,然后将池化结果中的每个值都填入其对应于原始数据区域中的相应位置即可

最大池化的反池化会复杂一些。要求在池 化过程中记录最大激活值的坐标位置,然后在反 池化时,只把池化过程中最大激活值所在位置坐 标的值激活,其他的值置为0。当然,这个过程只 是一种近似。因为在池化的过程中,除了最大值 所在的位置,其他的值也是不为0的。
小证明:
也有人说平均池化:一定是不为0的像素点,否则把0像素点带上会增加分母,使得整体数值变低。这个意思应该是padding='SAME’时,系统补的0,而不是图像的像素点自带的0
右边和下边为补的0
代码如下:
import tensorflow as tf
img = tf.constant([0.0,1.0,2.0,3.0,4.0,0.0,6.0,7.0,8.0,0.0,3,0,2.0,0.0,1.0,2.0,0.0,1.0,2.0,3.0,7.0,8.0,0.0,4.0,2.0])
print(img.shape)
value = tf.reshape(img, [ 1,5,5,1])
ksize = [1, 2,2, 1]
pool = tf.nn.avg_pool(value, ksize, strides=[1, 2, 2, 1], padding='SAME')
with tf.Session() as sess:
# 初始化变量
op_init = tf.global_variables_initializer()
sess.run(op_init)
print("value的值为:")
print(sess.run(value))
print("池化值为:")
print(sess.run(pool))
结果:
value的值为:
[[[[0.]
[1.]
[2.]
[3.]
[4.]]
[[0.]
[6.]
[7.]
[8.]
[0.]]
[[3.]
[0.]
[2.]
[0.]
[1.]]
[[2.]
[0.]
[1.]
[2.]
[3.]]
[[7.]
[8.]
[0.]
[4.]
[2.]]]]
池化值为:
[[[[1.75]
[5. ]
[2. ]]
[[1.25]
[1.25]
[2. ]]
[[7.5 ]
[2. ]
[2. ]]]]