Lumerical官方案例、FDTD时域有限差分法仿真学习（十五）——y分支的逆向设计（Inverse design of y-branch）

来自 https://support.lumerical.com/hc/en-us/articles/360042305274

使用内置参数优化 (parametric optimization ，PO) 方法对绝缘体上硅 Y 分支进行逆向设计，以实现最大宽带传输。 varFDTD 2.5D 求解器现在支持这种技术，允许实现真实的材料模型和单片平面器件。 伴随方法（adjoint method）是有效优化算法的基础，与粒子群（particle swarm）等其他优化方法相比，它显著减少了收敛所需的迭代次数。 然后将最佳设计导出到 GDS 文件中，以供进一步模拟和/或制造。

一、概述
了解模拟工作流程和关键结果

Lumerical 的逆向设计能力通过将基于梯度的优化程序的力量与麦克斯韦方程的基本属性中发现的效率相结合，提供了无与伦比的优化性能。 此示例将演示如何使用逆向设计方法生成 Y 分支形状，以提供近乎完美的传输效率。 此外，我们将演示如何使用您的参数修改示例，以便您可以将这种方法重用于您自己的设计。

此示例广泛借鉴了 LumOpt 框架：

•Git
•Documentation

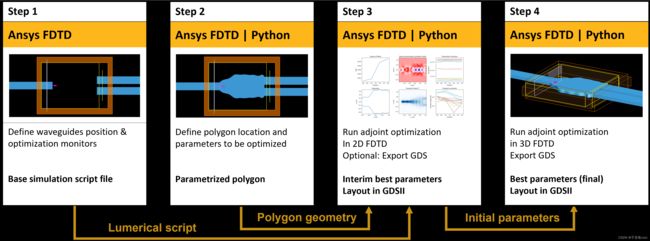
第 1 步：定义基本模拟参数

此初始步骤的目标是定义将用于伴随优化的 varFDTD 模拟的静态输入（static inputs）。 输入/输出波导的关键模拟设置、场梯度（field gradient）监视器和品质因数 (figure of merit，FOM) 计算、源（source）和网格（mesh）都经过参数化，以便于运行优化程序。 可以通过以下任一方式提供这些必要的参数

•模式项目文件
•lumerical 脚本（.lsf 格式）
•Python 函数句柄（function handle）。

第 2 步：定义可优化的几何图形

第二步是定义一个参数化的多边形几何形状，它将代表连接输入和输出波导的 Y 分支的主体（优化的几何形状）。 这是通过一个 python 函数完成的，该函数接受一组优化参数并在基础模拟中生成相应的多边形几何。 初始优化参数值及其限制也将在此步骤中定义。

第 3 步：在 2.5D 中运行参数优化

使用基本模拟和参数化多边形对象作为输入运行优化 python 脚本。这将是一个 2.5D 模拟，用于快速交付接近最优的设计，可用作下一步 3D 优化的初始猜测。为了找到定义最佳 Y 分支形状的最佳参数集，优化例程将使用指定的场监视器来计算：

•场梯度（the field gradients）：由优化区域几何形状的微小变化引起的介电常数扰动引起的场梯度
•品质因数 (FOM) 的梯度：由于形状变化，模式与波导的基本 TE 模式重叠的梯度

优化后，优化后的 Y 分支组件形状将导出为 GDSII 格式，可用于进一步的模拟和/或制造（掩模设计）。

第 4 步：在 3D 中运行参数优化 [可选]

作为可选步骤，2.5D 优化找到的最佳解决方案可用作 3D 优化的初始猜测，以验证 2.5D 仿真结果并在可能的情况下进一步提高设计性能。如果没有 varFDTD 许可证，则可以从 3D 优化开始；但是，如果没有初始解决方案，优化可能会进展缓慢。我们已经包括了对称边界条件，以将模拟时间减少四倍。

二、运行与结果
运行模型的说明和关键结果的讨论

第 1 步：定义基本模拟参数

1.在 Lumerical 环境中打开 python 脚本文件（varFDTD_y_branch.py）。 运行此脚本将导入构建模拟输入的 python 模块 y_branch_init_。 或者，假设已指定 Lumerical 的 python 模块的路径，可以从命令行或其 python 环境运行此脚本。
2.打开 MODE 会话后，它将设置基本模拟。 这样做是为了确保可以在(varFDTD_y_branch.py) 中更改的输入参数正确。 这是作为健全性检查完成的，不需要为下一步保存生成的模拟； 但是，可以更改此文件并将其用作优化脚本的输入。

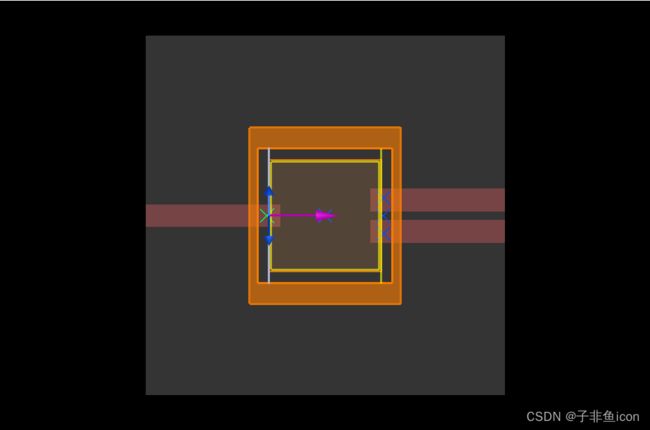
生成的基础模拟包括 varFDTD 模拟区域、（非色散）材料、源、监视器、可优化几何形状的网格覆盖以及输入和输出波导，如下图所示。

第 2 步：定义可优化的几何图形

如果您想按原样运行示例，则此步骤不是必需的，但是根据您的需要修改可优化的几何图形是必需的。

1.在脚本编辑器中打开 python 脚本文件 (y_branch_opt_2D.py)
2.通过数组initial_points_y定义优化的输入参数的初始值（可优化多边形的节点的Y坐标）
3.在数组范围内定义优化参数的范围
4.对优化参数进行任何其他必要的修改。 有关这些参数的更多信息，请参阅“重要模型设置”（Important model settings）
5.保存脚本

下面是优化 python 脚本的屏幕截图，显示了您可以在其中定义初始参数及其绑定值的行。 第二个图显示了基于默认初始参数的模拟中的可优化几何。


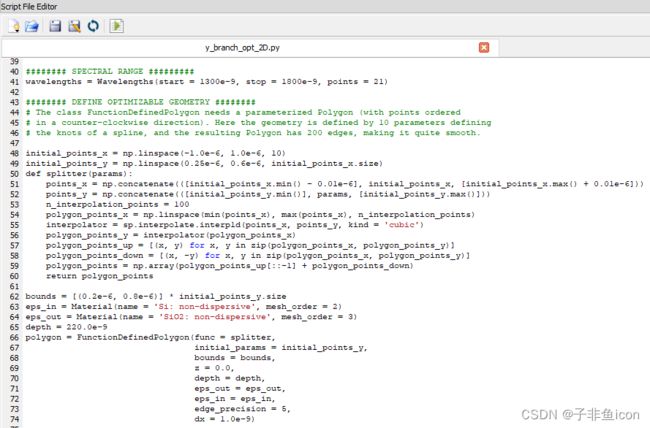
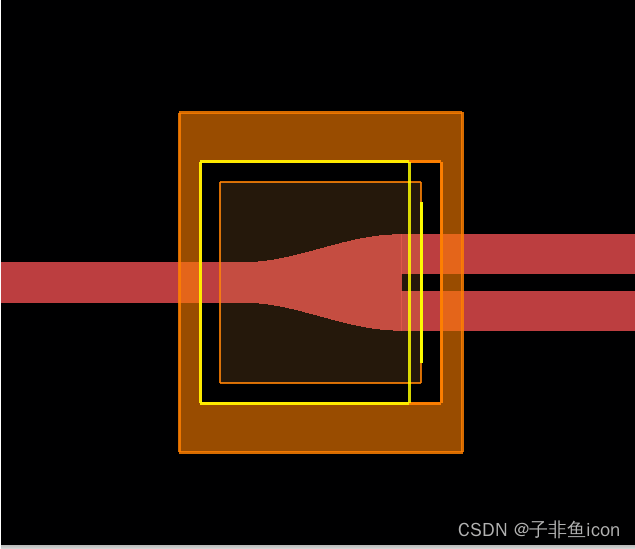
优化 python 脚本文件还将在优化结束时将优化设计导出到 GDS 文件。 GDS 文件将保存在与示例文件相同的文件夹中。 示例文件附带 GDS 导出操作所需的扩展名为 .lsfx 的加密脚本文件。 它们应保存在与 python 脚本文件相同的位置。

第 3 步：在 2.5D 中运行参数优化

1.在运行优化之前，请确保 API 的当前工作目录设置为示例文件所在的位置
2.从 MODE 中的脚本编辑器运行优化脚本文件。 或者，您可以使用 Lumerical installation提供的 Python 可执行文件从命令行运行优化脚本。

将打开一个命令提示符（在 Windows 操作系统中）或终端（在 macOS 或 Linux 中）窗口，显示优化的进度。 优化结束时的命令提示窗口截图如下所示，其中包含有关优化进度的信息。

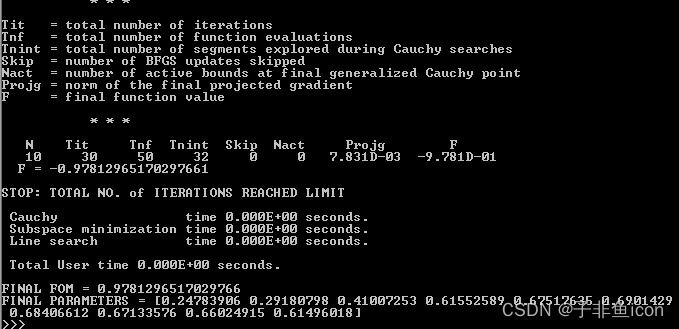
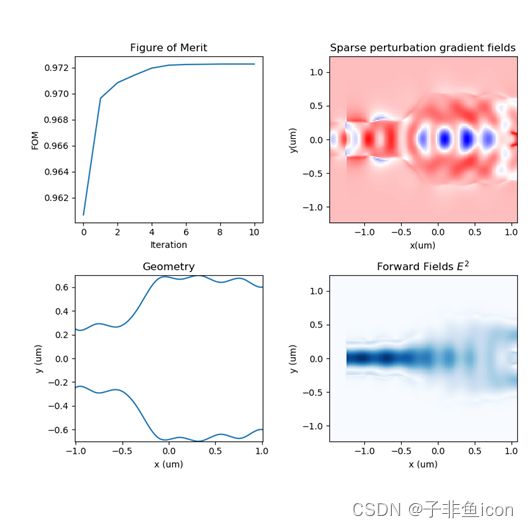
在优化过程中，优化例程将打开几个新的 varFDTD 会话，以根据优化算法的猜测执行模拟。这些 CAD 窗口可以通过在优化器中指定“hide_fdtd_cad=true”来隐藏。另一个窗口还将报告优化进度，提供优化几何演变、品质因数、参数和其他相关信息的各种图。下图显示了优化过程结束时的优化报告窗口。最终解决方案的几何形状可以在图中看到，它表明 FOM 在大约 25 次迭代后几乎没有改善，这表明迭代次数可以进一步减少以供未来运行。图中还可以看到设备结构内的场梯度（由于几何形状的变化）和正向场分布。此外，很明显，优化参数值的变化在几次迭代后变得不那么强烈，因为 FOM 越来越接近最优值。随着迭代的继续，FOM 梯度的变化（基于参数值的变化）也平均减少，如梯度演化图中所示。

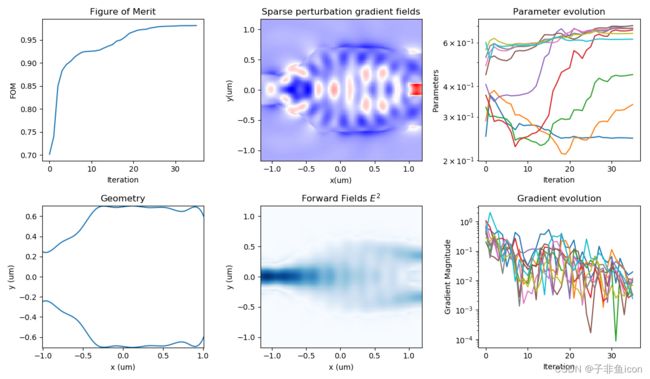
在优化结束时，最终的参数值将保存在与示例文件相同文件夹中的文本文件 (2D_parameters.txt) 中，示例文件将用于下一步的 3D 优化。 此外，每次迭代的模拟文件副本、包含每次迭代的参数历史和 FOM 值的文本文件以及每次迭代的优化报告窗口的静止图像都将保存在一个文件夹中（名称以“ opts”开头）与示例文件位于同一文件夹中，以供将来参考。 每次优化运行都会创建一个名称相同但带有编号后缀的新文件夹，以避免覆盖以前的运行数据。 最后，我们获得了 FOM 约为 0.9811 的 2.5D 设计。

这是在 2.5D 中优化的几何图形：

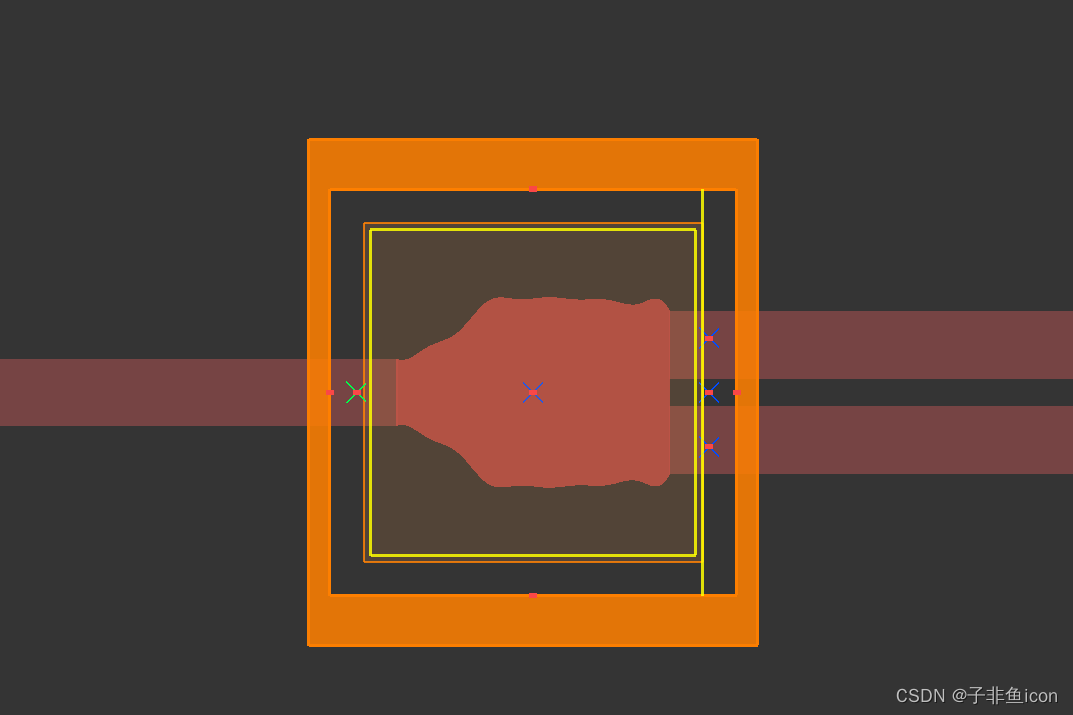
优化 python 脚本文件还将在优化结束时将优化设计导出到 GDS 文件。 GDS 文件将保存在与示例文件相同的文件夹中。 示例文件附带 GDS 导出操作所需的扩展名为 .lsfx 的加密脚本文件。 它们应保存在与 python 脚本文件相同的位置。

第 4 步：在 3D 中运行参数优化 [可选]

1.在 FDTD 脚本编辑器中打开并运行优化 python 脚本文件 (y_branch_opt_3D.py)。 或者，您可以使用 Lumerical installation提供的 Python 可执行文件从命令行运行优化脚本。 如果可用，此脚本将从 2.5D 优化中读取最终参数（存储在 2D_parameters.txt 中）。 否则，它将以脚本中设置的默认值开始。 这将调用文件 FDTD_y_branch.py 文件中定义的 python 模块来设置模拟。

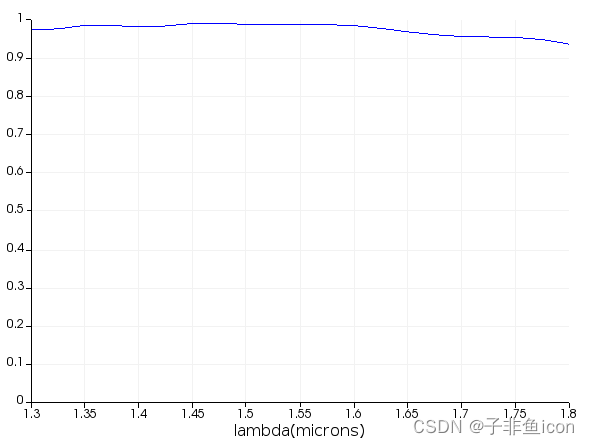
查看 3D 优化的结果会发现，通过 3D 模拟预测 Y 分支的透射率约为 94%（这比预测值为 98% 的 2D 情况更真实），并在优化结束时已提高到超过 95%。


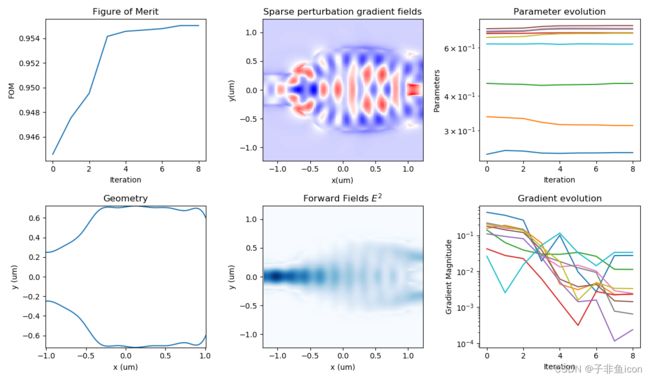
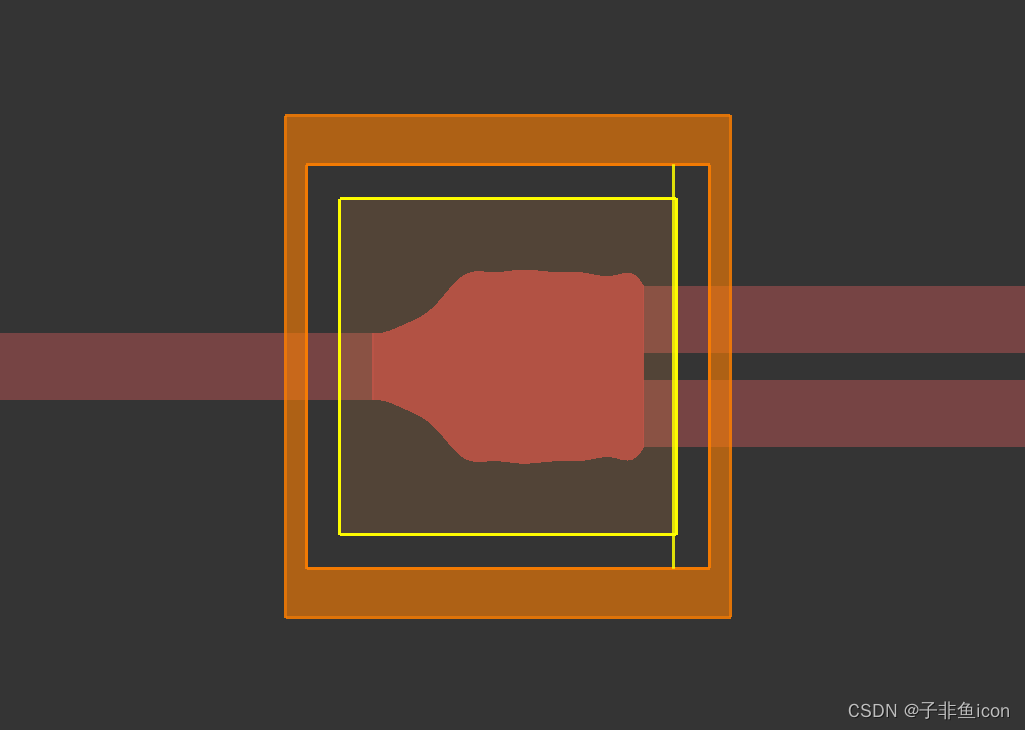
下图显示了从 1300 到 1800nm 之间优化的 3D 结构获得的最终宽带传输：

三、重要的模型设置
此模型中使用的重要对象和设置的描述

可优化几何的定义：可优化几何定义为一个多边形，其边界点的 x 坐标具有固定值，并且可以修改点的 y 坐标以获得最佳几何。这些 y 坐标被定义为三次样条的节点（如附录部分appendix section中的图所示），这使得对这些点进行三次样条插值以获得平滑的多边形几何成为可能。

优化场监视器位置：优化场 DFT 监视器 (opt_field) 用于收集可优化几何结构内的场数据，然后用于计算优化算法中使用的场梯度。因此，此监视器的位置非常重要，应该涵盖整个可优化的几何形状。

品质因数场监视器位置：由于该监视器用于计算优化所需的品质因数（模式与波导的基本 TE 模式重叠），因此它应位于 Y 分支的输出波导内。

可优化几何结构与基础模拟的尺寸：重要的是确保可优化几何结构的尺寸和基础模拟中设置的输入输出波导匹配，以便正确形成 Y 分支几何结构。

几何对象的高度：几何对象的高度（深度）应在基础模拟（输入、输出波导）和可优化几何（多边形）中匹配。这对于 3D 模拟以确保正确的几何设置尤其重要。对于波导，这是通过初始化方法（通过设置它们的 z 跨度）设置的，对于多边形，它在调用分离器函数以形成可优化几何图形时作为输入参数“深度”（depth）进行调整。

优化参数界限和初始值：优化算法允许改变参数的范围以及作为起点的这些参数的初始值定义如下：

initial_points_x = np.linspace(-1.0e-6, 1.0e-6, 10)
initial_points_y = np.linspace(0.25e-6, 0.6e-6, initial_points_x.size)
bounds = [(0.2e-6, 0.8e-6)] * initial_points_y.size

注意：这里选择线性锥度来设置初始 (x,y) 点，但也可以使用其他形状进行初始化。

模拟带宽：逆向设计 PO 方法支持宽带模拟。 使用由给定间隔中的频点数补充的起始和终止波长来定义带宽。 定义 FOM 时，波长规范会传递给优化脚本。 因此，基本模拟脚本中定义的波长设置将被覆盖。

此外，每个频点都可以独立指定其目标 FOM。 这意味着优化例程可以将自定义 FOM 配置文件作为波长的函数进行匹配，而不是简单地在整个带宽上最大化 FOM。

下面是这个 Y 分支示例的代码部分，它指定了从 1300 到 1800nm 的带宽，具有 21 个频率点：

wavelengths = Wavelengths(start = 1300e-9, stop = 1800e-9, points = 21)

然后在 FOM 定义期间将带宽设置传递给优化例程。 请注意，我们将所有频率点的 FOM 目标指定为 1，以最大化所需带宽上的传输：

fom = ModeMatch(monitor_name = 'fom',
                mode_number = 'fundamental mode',
                direction = 'Forward',
                target_T_fwd = lambda wl: np.ones(wl.size),
                norm_p = 1)

最大迭代次数：虽然算法有能力在品质因数的梯度低于某个阈值时停止优化，但用于定义优化算法的“max_iter”变量可用于限制迭代次数 算法能够执行。

对称：从 2019a r4 开始，逆向设计 PO 方法支持对称边界。 这对于 3D 模拟特别有用，它可以将模拟时间减少 4 倍。

四、使用您的设备参数更新模型
根据您的设备参数更新模型的说明

几何形状：如果您需要为 Y 分支定义自己的几何形状，包括 SOI 器件层厚度thickness（波导高度waveguide height）、输出波导间距(spacing)、器件长度（输入和输出波导之间的间距）和波导宽度(width)，应进行相应更改在基本模拟设置脚本和/或优化设置 python 脚本中。这可能需要更改基础脚本中的对象跨度和位置，Python 脚本中多边形的“深度depth”参数，其值也传递到脚本的 GDS 导出部分。源、模拟区域、网格覆盖、场梯度和 FOM 监视器尺寸也应相应调整，以确保它们正确覆盖整个结构。可能需要调整可优化几何形状在连接到输出波导的点处的初始值和边界的坐标，以确保可优化区域和波导之间的正确连接。此外，可优化几何的 x 坐标范围可能需要在优化设置 python 脚本中进行调整，其中分离器splitter函数定义如下所示（points_x 变量），以确保其正确连接到波导：

def splitter(params):
    points_x = np.concatenate(([initial_points_x.min() - 0.01e-6], initial_points_x, [initial_points_x.max() + 0.01e-6]))
    points_y = np.concatenate(([initial_points_y.min()], params, [initial_points_y.max()]))
    n_interpolation_points = 100
    polygon_points_x = np.linspace(min(points_x), max(points_x), n_interpolation_points)
    interpolator = sp.interpolate.interp1d(points_x, points_y, kind = 'cubic')
    polygon_points_y = interpolator(polygon_points_x)
    polygon_points_up = [(x, y) for x, y in zip(polygon_points_x, polygon_points_y)]
    polygon_points_down = [(x, -y) for x, y in zip(polygon_points_x, polygon_points_y)]
    polygon_points = np.array(polygon_points_up[::-1] + polygon_points_down)
    return polygon_points

建议设置坐标，使可优化区域和波导边缘之间有轻微的重叠，以确保它们在模拟中连接。

材料Materials：模拟中包含的材料（构成可优化几何形状的材料及其周围的材料）在步骤 1 中通过 lsf、项目文件或 python 函数定义。 在本例中，我们采用了所需模拟波长 1550nm 处的硅和二氧化硅的折射率。 应该确保初始化中定义（或给定折射率）的材料与定义几何时传递给优化器的材料相同，如下所示：

eps_in = Material(name = 'Si: non-dispersive', mesh_order = 2)
eps_out = Material(name = 'SiO2: non-dispersive', mesh_order = 3)
depth = 220.0e-9
polygon = FunctionDefinedPolygon(func = splitter,
    initial_params = initial_points_y,
    bounds = bounds,
    z = 0.0,
      depth = depth,
    eps_out = eps_out,
     eps_in = eps_in,
    edge_precision = 5,
     dx = 1.0e-9)

使用 varFDTD 现在可以使用材料库来定义材料属性； 然而，优化技术尚未经过色散材料的测试； 因此，有效折射率在中心频率处求解并传递给优化器。

五、让模型更进一步

为想要进一步定制模型的用户提供的信息和提示

此示例提供了预定义的多边形几何图形，该几何图形已经参数化并随后进行了优化以创建最终的 Y 分支形状。虽然多边形几何允许一些基本的自定义，例如 y 方向的边界，但高级用户可以修改 python 函数“splitter”来实现自定义参数化几何的属性（有时称为 pCell）。

样条节点数量：优化参数的数量对应于控制几何形状的样条节点数量。更多的节点将允许以更小的最小曲线半径对整体形状进行更细微的控制。另一方面，制造过程可能会限制最小特征尺寸，大量参数也可能转化为更长的优化时间。更改样条节点的数量需要修改splitter函数以及边界数组大小和传递给优化例程的初始参数。

自定义 pCell ：如何将标量参数数组转换为多边形（polygon）形状几乎有无限种可能性。因此，高级 Python 用户可以利用语言的健壮性，从头开始编写splitter函数。唯一的限制是输入是标量数组，输出是一组多边形点。下面的示例显示了一个示例函数，该函数不仅参数化了 Y 分支的主体，而且还参数化了输出波导：

def splitter(params = np.linspace(0.25e-6, 2e-6, 20)):
    ''' Defines a taper where the paramaters are the y coordinates of the nodes of a cubic spline. '''
    points_x = np.concatenate(([-2.51e-6], np.linspace(-2.5e-6,2.5e-6,20), [2.51e-6]))
    points_y = np.concatenate(([0.25e-6], params, [2e-6]))
    n_interpolation_points = 100
    px = np.linspace(min(points_x), max(points_x), n_interpolation_points)
    interpolator = sp.interpolate.interp1d(points_x, points_y, kind = 'cubic')
    py = interpolator(px)
    py = np.minimum(2.5e-6, py)
    py = np.maximum(np.concatenate((np.ones(50)*0.2e-6, np.ones(50)*0.53e-6)), py)
    px = np.concatenate((px, px[40::][::-1]))
    py = np.concatenate((py, py[40::][::-1]-0.5e-6))
    polygon_points_up = [(x, y) for x, y in zip(px, py)]
    polygon_points_down = [(x, -y) for x, y in zip(px, py)]
    polygon_points = np.array(polygon_points_up[::-1] + polygon_points_down)
    return polygon_points

演示修改后 pCell 优化进度的视频：

注意：确保基础模拟的属性与修改后的 pCell 相对应很重要。 例如，当您修改 pCell 尺寸时，需要相应地修改波导和监视器的尺寸和位置。 阅读重要的模型设置以获取更多信息。

六、其他资源

其他文档、示例和培训材料

•Python API
•Y Branch PSO
•Y Branch S parameter extraction
•Symmetric boundary conditions
•Inverse design of waveguide crossing
•Inverse design of grating coupler

七、附录：参数优化（伴随方法）
其他背景信息和理论

在典型的器件优化中，目标是最小化或最大化品质因数F§，其取决于一组 N 个设计参数 p=(p1,…,pn) 。 品质因数可以是用于对设备性能进行基准测试的任何量，而设计参数可以是改变设备响应的任何量。 为了针对给定的一组 p 值评估 F§，使用基于物理的建模工具（例如 FDTD）将 p 值映射到 F 值。模型通常包含对设备几何形状、材料和所有相关的环境条件。 在参数化形状优化中，目标是允许设备几何形状的某些部分发生变化，以最小化或最大化品质因数。 为此，通常定义形状函数 f§ 以指定设备几何的一部分； 一个例子如下图所示：

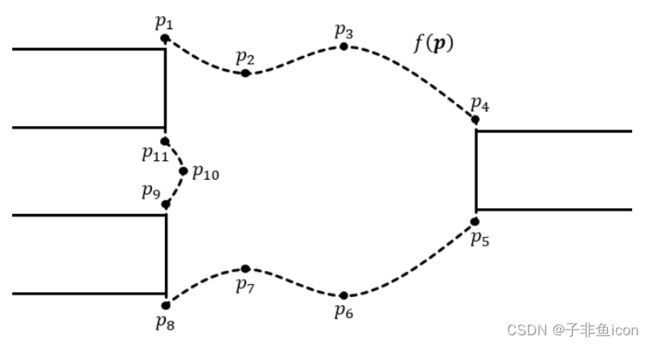
使用连接样条定义的具有参数化交界边界 f§ 的 Y 拆分器。

形状函数通常是用户定义的，必须提供给建模工具以构建设备的几何形状。 一旦可以针对给定的形状函数评估品质因数 F(f§)，最小化器就可以对品质因数进行多次评估以找到最佳形状。 有大量的最小化工具和技术可用于尝试找到最佳形状参数。 在选择最小化技术时，重要的是要考虑运行设备仿真来评估品质因数可能是一个缓慢的操作。 因此，最适合的最小化技术是那些限制品质因数评估次数的技术。 有了一个好的起点，基于梯度的方法可以通过相对较少的品质因数评估快速找到最优参数，前提是也可以评估品质因数的梯度：

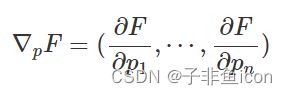
为了在不必对每个偏导数执行一次模拟的情况下评估梯度，可以采用一种称为伴随方法（adjoint method）的技术。 该技术利用线性偏微分方程的特性，仅使用两个模拟来评估梯度，而与优化参数的数量无关。 FDTD (lumopt) 中基于 Python 的形状优化模块允许用户定义形状函数并运行相应的器件仿真来评估品质因数。 该模块还实现了伴随方法来提供梯度。这样，SciPy 优化模块中的任何基于梯度的最小化器都可以用于执行全自动优化。