【NumPy教程】（快速入门版）

转载于：http://c.biancheng.net/numpy/

NumPy 是 Numerical Python 的缩写，它是一个由多维数组对象（ndarray）和处理这些数组的函数（function）集合组成的库。使用 NumPy 库，可以对数组执行数学运算和相关逻辑运算。NumPy 不仅作为 Python 的扩展包，它同样也是 Python 科学计算的基础包。

这套《Python NumPy教程》讲解了 NumPy 的基础知识，比如 NumPy 的架构、NumPy 数组的常用函数，以及不同索引类型的使用方法等。在本教程的最后，我们讲解了 NumPy 与 Matplotlib 的组合使用。为了便于大家更好地学习，在教程中大量地使用了知识点与示例相结合的方式。

读者

本教程是为那些想学习 NumPy 基础知识的初学者准备的，当您在学习完成本教程之后，您的知识水平将得到一定程度的提升，您可以在此基础上进一步学习与 NumPy 相关联的软件包，比如 Pandas、Matplotlib。

阅读条件

在学习本套教程之前，您应该对计算机编程有基本的了解，并掌握 Python 编程语言的基础知识，这都将有助于您学习本套教程。

NumPy是什么

NumPy 的全称是“ Numeric Python”，它是 Python 的第三方扩展包，主要用来计算、处理一维或多维数组。

在数组算术计算方面， NumPy 提供了大量的数学函数。NumPy 的底层主要用 C语言编写，因此它能够高速地执行数值计算。NumPy 还提供了多种数据结构，这些数据结构能够非常契合的应用在数组和矩阵的运算上。

NumPy 的前身是 Numeric 程序包，该包由 Jim Hugunin 开发，在这之后，他还开发了另一个类似的的程序包 Numarray，相比前者而言 Numarray 具有更加全面的功能 。在 2005 年，Travis Oliphant 通过整合 Numarray 与 Numeric 软件包的功能，从而集成了 NumPy。NumPy 的最新版本 1.19.2 已于 2020 年 9 月10 日发布。

NumPy 作为一个开源项目，它由许多协作者共同开发维护，这也是 NumPy 的优势之一。

NumPy使用需求

随着数据科学（Data Science，简称 DS，包括大数据分析与处理、大数据存储、数据抓取等分支）的蓬勃发展，像 NumPy、SciPy（Python科学计算库）、Pandas（基于NumPy的数据处理库） 等数据分析库都有了大量的增长，它们都具有较简单的语法格式。

在矩阵乘法与数组形状处理上，NumPy 有着非常不错的性能，再加上 NumPy 的计算速度很快，这些都是 NumPy 成为一款数据分析工具的重要原因。

数组形状可以理解为数组的维度，比如一维数组、二维数组、三维数组等；以二维数组为例，改变数组形状就是交换数组的行和列，也即将数组旋转 90 度。

NumPy 可以很便捷高效地处理大量数据，那么使用 NumPy 做数据处理有哪些优点呢？总结如下：

• NumPy 是 Python 科学计算基础库；
• NumPy 可以对数组进行高效的数学运算；
• NumPy 的 ndarray 对象可以用来构建多维数组；
• NumPy 能够执行傅立叶变换与重塑多维数组形状；
• NumPy 提供了线性代数，以及随机数生成的内置函数。

NumPy应用场景

NumPy 通常与 SciPy（Python科学计算库）和 Matplotlib（Python绘图库）等软件包组合使用，这种组合方式被用来广泛地代替 MatLab 的使用。

MatLab 是一款强大的数学计算软件，广泛应用在数据分析、电子通信、深度学习、图像处理、机器视觉、量化金融等领域，但近些年随着 Python 语言的迅猛发展，Python 被看作是一种更适合代替 MatLab 的编程语言。您可以使用 NumPy、SciPy 与 Matplotlib 等 Python 工具包搭建科学计算环境，比如 Anaconda 就是是一个开源的 Python 发行版本，它包含了 Python 、NumPy 等 180 多个科学包及其依赖项。

因为 NumPy 是 Python 的扩展程序包，所以您在学习 NumPy 之前应该具备一些 Python 基础知识，这对本教程的学习将大有裨益。如果您想了解关于 NumPy 更多的知识可浏览 NumPy 官网（https://numpy.org/）。

NumPy下载与安装

NumPy 是 Python 的第三方扩展包，但它并没有包含在 Python 标准库中，因此您需要单独安装它。本节介绍如何在不同的操作系统上安装 NumPy。

Windows系统安装

在 Windows 系统下安装 NumPy 有两种常用方式，下面分别对其进行介绍。

使用 Python 包管理器pip来安装 NumPy，是一种最简单、最轻量级的方法。只需执行以下命令即可：

pip install numpy

在实际项目中， NumPy 通常与 SciPy 程序包一起使用，SciPy 可以看做对 NumPy 库的扩展，它在 NumPy 的基础上又增加了许多工程计算函数。因此将它们同时安装是一个不错的选择。但如果你只想针对 NumPy 进行学习，可以不用考虑这种安装方法。

注意：在 Windows 下直接使用 pip 安装 SciPy 会发生报错，需要我们解决 SciPy 的依赖项问题，所以不推荐使用pip安装 SciPy 程序包。下面介绍如何使用 SciPy 栈安装。

首先我们要知道什么是 SciPy 栈？其实它是一个科学计算软件包的集成平台，这类平台囊括了常用的数值计算与机器学习库，比如 NumPy、Matplotlib、SciPy 库、IPython 等，并且它可以自动解决包之间的依赖问题。通过安装一个集成平台就可以实现上述所有软件包的安装，何乐而不为呢

下面介绍几种常用的 SciPy 栈，主要有以下几种：

Anaconda（官网下载：https://www.anaconda.com/）是一个开源的 Python 发行版，它包含了 NumPy、SciPy 等180多个科学包及其依赖项。除了支持 Windows 外，也支持 Linux 和 Mac 系统。Anaconda 就目前应用较为广泛，因此建议安装。

Anaconda 的下载文件约 500 MB 左右，你可以选择安装 Miniconda，它是 Anaconda 的轻巧版，只需 40 余兆。

图1：Anaconda官网下载图（点击看高清图）

Python(x,y)（下载地址：https://python-xy.github.io/）是一款基于 Python、Qt （图形用户界面）和 Spyder （交互式开发环境）开发的软件，主要用于数值计算、数据分析和数据可视化等工程项目，目前只支持 Python 2 版本。

Pyzo（下载地址：https://pyzo.org/）是一个跨平台 Python IDE，基于 Python 3 编写，非常适合科学计算，它设计的宗旨就是为了简化和提供效率。

WinPython（下载地址：https://sourceforge.net/projects/winpython/files/）免费的 Python 发行版，包含了常用的科学计算包与 Spyder IDE 开发环境，但仅支持 Windows 系统。

MacOSX系统安装

Mac 系统虽然自带包管理器Homebrew，但是它不能下载 NumPy 等科学计算包，所以需要使用下列方式安装：

$ pip3 install numpy scipy matplotlib -i https://pypi.tuna.tsinghua.edu.cn/simple

注意：-i 参数后指的是国内下载源，加快下载的速度。

Linux系统安装

在 Linux 系统中，您可以选择只单独安装 NumPy 一个软件包，也可以同时安装多个软件包。下面介绍了不同的 Linux 发行版具体的安装命令，如下所示：

1) Ubuntu/Debian

对于 Ubuntu/Debian 系统，可以在终端上执行以下命令：

$ sudo apt-get install python-numpy python-scipy python-matplotlib ipython ipython-notebook python-pandas python-sympy python-nose 

2) Redhat/CentOS

在 Redhat/CentOS 系统上执行以下命令来安装 NumPy 与其它科学计算包：

$ sudo yum install numpy scipy python-matplotlib ipython python-pandas sympy python-nose

注意：不同的软件包之间必须使用“一个空格”隔开。

最后验证是否安装成功，如下所示：

打开 Python 交互解释器 ，并导入 NumPy 模块，如下图 2 所示如果未出现错误提示，则表示已安装成功。

图2：Numpy安装成功

注意：这里是以 Windows 系统为例进行验证的，Linux 验证方式与其相同。

NumPy ndarray对象

NumPy 定义了一个 n 维数组对象，简称 ndarray 对象，它是一个一系列相同类型元素组成的数组集合。数组中的每个元素都占有大小相同的内存块，您可以使用索引或切片的方式获取数组中的每个元素。

ndarray 对象有一个 dtype 属性，该属性用来描述元素的数据类型，相关知识会在《NumPy数据类型》一节做详细介绍 。

ndarray 对象采用了数组的索引机制，将数组中的每个元素映射到内存块上，并且按照一定的布局对内存块进行排列，常用的布局方式有两种，即按行或者按列。

创建ndarray对象

通过 NumPy 的内置函数 array() 可以创建 ndarray 对象，其语法格式如下：

numpy.array(object, dtype = None, copy = True, order = None,ndmin = 0)

下面表格对其参数做了说明：

序号	参数	描述说明
1	object	表示一个数组序列。
2	dtype	可选参数，通过它可以更改数组的数据类型。
3	copy	可选参数，表示数组能否被复制，默认是 True。
4	order	以哪种内存布局创建数组，有 3 个可选值，分别是 C(行序列)/F(列序列)/A(默认)。
5	ndim	用于指定数组的维度。

创建一维数组：

a=numpy.array([1,2,3])

示例代码：

import numpy
a=numpy.array([1,2,3])#使用列表构建一维数组
print(a)
[1 2 3]
print(type(a))
#ndarray数组类型
<class 'numpy.ndarray'>

创建多维数组：

b=numpy.array([[1,2,3],[4,5,6]])

示例代码：

b=numpy.array([[1,2,3],[4,5,6]])
print(b)
[[1 2 3]
[4 5 6]]

如果要改变数组元素的数据类型，可以使用通过设置 dtype，如下所示：

c=numpy.array([2,4,6,8],dtype=“数据类型名称”)

现在将 c 数组中的元素类型变成了复数类型：

c=numpy.array([2,4,6,8],dtype="complex")
print(c)
[2.+0.j 4.+0.j 6.+0.j 8.+0.j]

array() 是创建 ndarray 对象的基本方法，在后续内容中还会介绍其他方法。

ndim查看数组维数

通过 ndim 可以查看数组的维度：

import numpy as np 
arr = np.array([[1, 2, 3, 4], [4, 5, 6, 7], [9, 10, 11, 23]]) 
print(arr.ndim) 
2

您也可以使用 ndim 参数创建不同维度的数组：

#输出一个二维数组
import numpy as np
a = np.array([1, 2, 3,4,5], ndim = 2)
print(a)

输出结果如下：

[[1 2 3 4 5]]

reshape数组变维

数组的形状指的是多维数组的行数和列数。Numpy 模块提供 reshape() 函数可以改变多维数组行数和列数，从而达到数组变维的目的。因此数组变维即对数组形状的重塑，如图1所示：

图1：reshape函数数组变维

reshape() 函数可以接受一个元组作为参数，用于指定了新数组的行数和列数，示例如下：

import numpy as np 
e = np.array([[1,2],[3,4],[5,6]]) 
print("原数组",e) 
e=e.reshape(2,3) 
print("新数组",e)  

输出如下：

原数组 [[1 2]
[3 4]
[5 6]]
新数组 [[1 2 3]
[4 5 6]]

NumPy数据类型

NumPy 作为 Python 的扩展包，它提供了比 Python 更加丰富的数据类型，如表 1 所示：

序号	数据类型	语言描述
1	bool_	布尔型数据类型（True 或者 False）
2	int_	默认整数类型，类似于 C 语言中的 long，取值为 int32 或 int64
3	intc	和 C 语言的 int 类型一样，一般是 int32 或 int 64
4	intp	用于索引的整数类型（类似于 C 的 ssize_t，通常为 int32 或 int64）
5	int8	代表与1字节相同的8位整数。值的范围是-128到127。
6	int16	代表 2 字节（16位）的整数。范围是-32768至32767。
7	int32	代表 4 字节（32位）整数。范围是-2147483648至2147483647。
8	int64	表示 8 字节（64位）整数。范围是-9223372036854775808至9223372036854775807。
9	uint8	代表1字节（8位）无符号整数。
10	uint16	2 字节（16位）无符号整数。
11	uint32	4 字节（32位）的无符号整数。
12	uint64	8 字节（64位）的无符号整数。
13	float_	float64 类型的简写。
14	float16	半精度浮点数，包括：1 个符号位，5 个指数位，10个尾数位。
15	float32	单精度浮点数，包括：1 个符号位，8 个指数位，23个尾数位。
16	float64	双精度浮点数，包括：1 个符号位，11 个指数位，52个尾数位。
17	complex_	复数类型，与 complex128 类型相同。
18	complex64	表示实部和虚部共享 32 位的复数。
19	complex128	表示实部和虚部共享 64 位的复数。
20	str_	表示字符串类型
21	string_	表示字节串类型

数据类型对象

数据类型对象（Data Type Object）又称 dtype 对象，主要用来描述数组元素的数据类型、大小以及字节顺序。同时，它也可以用来创建结构化数据。比如常见的 int64、float32 都是 dtype 对象的实例，其语法格式如下：

np.dtype(object)

创建一个 dtype 对象可以使用下列方法：

a= np.dtype(np.int64)

示例：

import numpy as np 
a= np.dtype(np.int64) 
print(a)  

输出结果：

int64

数据类型标识码

NumPy 中每种数据类型都有一个唯一标识的字符码，如下所示：

字符	对应类型
b	代表布尔型
i	带符号整型
u	无符号整型
f	浮点型
c	复数浮点型
m	时间间隔（timedelta）
M	datatime（日期时间）
O	Python对象
S,a	字节串（S）与字符串（a）
U	Unicode
V	原始数据（void）

下面使用数据类型标识码，创建一组结构化数据：

#创建数据类型score
import numpy as np
dt = np.dtype([('score','i1')])
print(dt) 

输出如下：

[(‘score’, ‘i1’)]

将上述的数据类型对象 dt，应用到 ndarray 中：

#定义字段名score，以及数组数据类型i1
dt = np.dtype([('score','i1')])
a = np.array([(55,),(75,),(85,)], dtype = dt)
print(a)
print(a.dtype)
print(a['score'])

输出结果：

获取a数组：
[(55,) (75,) (85,)] 
数据类型对象dtype
dtype([('score', 'i1')])
获取'score'字段分数
[55 75 85]

定义结构化数据

通常情况下，结构化数据使用字段的形式来描述某个对象的特征。以下示例描述一位老师的姓名、年龄、工资的特征，该结构化数据其包含以下字段：

• str 字段：name
• int 字段：age
• float 字段：salary

定义过程如下：

import numpy as np
teacher = np.dtype([('name','S20'), ('age', 'i1'), ('salary', 'f4')])
#输出结构化数据teacher
print(teacher)
#将其应用于ndarray对象
b = np.array([('ycs', 32, 6357.50),('jxe', 28, 6856.80)], dtype = teacher) 
print(b)

输出结果：

[('name', 'S20'), ('age', 'i1'), ('salary', '

NumPy数组属性

本节介绍 Numpy 数组的常用属性。

ndarray.shape

shape 属性的返回值一个由数组维度构成的元组，比如 2 行 3 列的二维数组可以表示为(2,3)，该属性可以用来调整数组维度的大小。

示例如下，输出了数组的维度：

import numpy as np
a = np.array([[2,4,6],[3,5,7]])
print(a.shape)

输出结果：

(2,3)

通过 shape 属性修改数组的形状大小：

import numpy as np
a = np.array([[1,2,3],[4,5,6]])
a.shape = (3,2)
print(a)

输出结果：

[[1, 2]
[3, 4]
[5, 6]]

ndarray.reshape()

NumPy 还提供了一个调整数组形状的 reshape() 函数。

import numpy as np
a = np.array([[1,2,3],[4,5,6]])
b = a.reshape(3,2)
print(b)

输出结果：

[[1, 2]
[3, 4]
[5, 6]]

ndarray.ndim

该属性返回的是数组的维数，示例如下：

import numpy as np
#随机生成一个一维数组
c = np.arange(24)
print(c)
print(c.ndim)
#对数组进行变维操作
e = c.reshape(2,4,3)
print(e) 
print(e.ndim)

输出结果如下所示：

#随机生成的c数组
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
#c数组的维度
1
#变维后数组e
[[[ 0  1  2]
  [ 3  4  5]
  [ 6  7  8]
  [ 9 10 11]]

[[12 13 14]
  [15 16 17]
  [18 19 20]
  [21 22 23]]]
#e的数组维度
3

ndarray.itemsize

返回数组中每个元素的大小（以字节为单位），示例如下：

#数据类型为int8，代表1字节
import numpy as np
x = np.array([1,2,3,4,5], dtype = np.int8)
print (x.itemsize)

输出结果为：

1

#数据类型为int64，代表8字节
import numpy as np
x = np.array([1,2,3,4,5], dtype = np.int64)
print (x.itemsize)

输出结果：

8

ndarray.flags

返回 ndarray 数组的内存信息，比如 ndarray 数组的存储方式，以及是否是其他数组的副本等。

示例如下：

import numpy as np
x = np.array([1,2,3,4,5])
print (x.flags)

输出结果如下：

C_CONTIGUOUS : True
F_CONTIGUOUS : True
OWNDATA : True
WRITEABLE : True
ALIGNED : True
WRITEBACKIFCOPY : False
UPDATEIFCOPY : False

Numpy创建数组

在《NumPy Ndarray对象》一节，介绍了创建 ndarray 数组的基本方法，除了使用 array() 方法外，NumPy 还提供了其他创建 ndarray 数组的方法。本节对这些常用方法做简单介绍。

numpy.empty()

numpy.empty() 创建未初始化的数组，可以指定创建数组的形状（shape）和数据类型（dtype），语法格式如下：

numpy.empty(shape, dtype = float, order = ‘C’)

它接受以下参数：

• shape：指定数组的形状；
• dtype：数组元素的数据类型，默认值是值 float；
• order：指数组元素在计算机内存中的储存顺序，默认顺序是“C”(行优先顺序)。

使用示例如下：

import numpy as np 
arr = np.empty((3,2), dtype = int) 
print(arr) 

输出结果：

[[2003134838  175335712]
[ 538976288  538976288]
[1970562418 1684369010]]

可以看到，numpy.empty() 返回的数组带有随机值，但这些数值并没有实际意义。切记 empty 并非创建空数组。

numpy.zeros()

该函数用来创建元素均为 0 的数组，同时还可以指定被数组的形状，语法格式如下：

numpy. zeros(shape,dtype=float,order=“C”)

参数名称	说明描述
shape	指定数组的形状大小。
dtype	可选项，数组的数据类型
order	“C”代表以行顺序存储，“F”则表示以列顺序存储

示例如下：

import numpy as np
#默认数据类型为浮点数
a=np.zeros(6)
print(a)
b=np.zeros(6,dtype="complex64" )
print(b)

输出结果：

#a数组
[0. 0. 0. 0. 0. 0.]
#b数组
[0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]

也可以使用自定义的数据类型创建数组，如下所示：

c = np.zeros((3,3), dtype = [('x', 'i4'), ('y', 'i4')]) 
print(c)
#输出x,y，并指定的数据类型
[[(0, 0) (0, 0) (0, 0)]
[(0, 0) (0, 0) (0, 0)]
[(0, 0) (0, 0) (0, 0)]]

numpy.ones()

返回指定形状大小与数据类型的新数组，并且新数组中每项元素均用 1 填充，语法格式如下：

numpy.ones(shape, dtype = None, order = ‘C’)

示例如下：

import numpy as np 
arr1 = np.ones((3,2), dtype = int) 
print(arr1)  

输出结果如下：

 [[1 1] [1 1] [1 1]]

下面介绍如何使用 Python 列表、流对象、可迭代对象来创建一个 NumPy 数组。

numpy.asarray()

asarray() 与 array() 类似，但是它比 array() 更为简单。asarray() 能够将一个 Python 序列转化为 ndarray 对象，语法格式如下：

numpy.asarray（sequence，dtype = None ，order = None ）

它接受下列参数：

• sequence：接受一个 Python 序列，可以是列表或者元组；
• dtype：可选参数，数组的数据类型；
• order：数组内存布局样式，可以设置为 C 或者 F，默认是 C。

示例 1，将列表转化为 numpy 数组：

import numpy as np 
l=[1,2,3,4,5,6,7] 
a = np.asarray(l); 
print(type(a)) 
print(a) 

输出结果如下所示：

#a数组类型

#a数组
[1 2 3 4 5 6 7]

示例 2，使用元组创建 numpy 数组：

import numpy as np 
l=(1,2,3,4,5,6,7)    
a = np.asarray(l); 
print(type(a)) 
print(a)  

输出结果如下：

[1 2 3 4 5 6 7]

示例 3，使用嵌套列表创建多维数组：

import numpy as np 
l=[[1,2,3,4,5,6,7],[8,9]] 
a = np.asarray(l); 
print(type(a)) 
print(a)  

输出结果：

[list([1, 2, 3, 4, 5, 6, 7]) list([8, 9])]

numpy.frombuffer()

表示使用指定的缓冲区创建数组。下面给出了该函数的语法格式：

numpy.frombuffer(buffer, dtype = float, count = -1, offset = 0)

它的参数说明如下所示：

• buffer：将任意对象转换为流的形式读入缓冲区；
• dtype：返回数组的数据类型，默认是 float32；
• count：要读取的数据数量，默认为 -1 表示读取所有数据；
• offset：读取数据的起始位置，默认为 0。

示例 4 如下：

import numpy as np 
#字节串类型
l = b'hello world' 
print(type(l)) 
a = np.frombuffer(l, dtype = "S1") 
print(a) 
print(type(a)) 

输出结果如下：

[b'h' b'e' b'l' b'l' b'o' b' ' b'w' b'o' b'r' b'l' b'd']

numpy.fromiter()

该方法可以把迭代对象转换为 ndarray 数组，其返回值是一个一维数组。

numpy.fromiter(iterable, dtype, count = -1)

参数说明如下：

参数名称	描述说明
iterable	可迭代对象。
dtype	返回数组的数据类型。
count	读取的数据数量，默认为 -1，读取所有数据。

示例5：使用内置 range() 函数创建列表对象，然后使用迭代器创建 ndarray 对象，代码如下：

import numpy as np
# 使用 range 函数创建列表对象 
list=range(6)
#生成可迭代对象i
i=iter(list)
#使用i迭代器，通过fromiter方法创建ndarray
array=np.fromiter(i, dtype=float)
print(array)

输出结果：

[0. 1. 2. 3. 4. 5.]

NumPy创建区间数组

所谓区间数组，是指数组元素的取值位于某个范围内，并且数组元素之间可能会呈现某种规律，比如等比数列、递增、递减等。

为了方便科学计算，Python NumPy 支持创建区间数组。

1. numpy.arange()

在 NumPy 中，您可以使用 arange() 来创建给定数值范围的数组，语法格式如下：

numpy.arange(start, stop, step, dtype)

参数说明见下表：

参数名称	参数说明
start	起始值，默认是 0。
stop	终止值，注意生成的数组元素值不包含终止值。
step	步长，默认为 1。
dtype	可选参数，指定 ndarray 数组的数据类型。

根据start与stop指定的范围以及step步长值，生成一个 ndarray 数组，示例如下。

import numpy as np
x = np.arange(8) 
print (x)

输出结果如下所示：

[0 1 2 3 4 5 6 7]

设置 start 、stop 值以及步长，最终输出 0-10 中的奇数：

import numpy as np
x = np.arange(1,10,2) 
print (x)

输出结果如下所示：

[1 3 5 7 9]

2. numpy.linspace()

表示在指定的数值区间内，返回均匀间隔的一维等差数组，默认均分 50 份，语法格式如下：

np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

参数说明如下：

• start：代表数值区间的起始值；
• stop：代表数值区间的终止值；
• num：表示数值区间内要生成多少个均匀的样本。默认值为 50；
• endpoint：默认为 True，表示数列包含 stop 终止值，反之不包含；
• retstep：默认为 True，表示生成的数组中会显示公差项，反之不显示；
• dtype：代表数组元素值的数据类型。

示例如下：

import numpy as np
#生成10个样本
a = np.linspace(1,10,10)
print(a)

输出结果：

[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.]

下面示例是 endpoint 为 Fasle 时，此时不包含终止值：

import numpy as np 
arr = np.linspace(10, 20, 5, endpoint = False) 
print("数组数值范围 ：",arr)  

输出结果如下：

数组数值范围 ： [10. 12. 14. 16. 18.]

retstep 参数使用示例如下：

import numpy as np
x = np.linspace(1,2,5, retstep = True)
print(x) 

输出结果如下，其中 0.25 为等差数列的公差：

(array([1. , 1.25, 1.5 , 1.75, 2. ]), 0.25)

3. numpy.logspace

该函数同样返回一个 ndarray 数组，它用于创建等比数组，语法格式如下：

np.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None)

其中 base 代表对数函数的底数，默认为 10，参数详细说明见下表：

参数名称	说明描述
start	序列的起始值：base**start。
stop	序列的终止值：base**stop。
num	数值范围区间内样本数量，默认为 50。
endpoint	默认为 True 包含终止值，反之不包含。
base	对数函数的 log 底数，默认为10。
dtype	可选参数，指定 ndarray 数组的数据类型。

使用示例如下：

import numpy as np
a = np.logspace(1.0,2.0, num = 10)
print (a)

输出结果：

[ 10.          12.91549665  16.68100537  21.5443469   27.82559402
  35.93813664  46.41588834  59.94842503  77.42636827 100.        ]

下面是 base = 2 的对数函数，示例如下：

import numpy as np
a = np.logspace(1,10,num = 10, base = 2)
print(a)

输出结果:

[ 2. 4. 8. 16. 32. 64. 128. 256. 512. 1024.]

Numpy索引和切片

在 NumPy 中，如果想要访问，或修改数组中的元素，您可以采用索引或切片的方式，比如使用从 0 开始的索引依次访问数组中的元素，这与 Python 的 list 列表是相同的。

NumPy 提供了多种类型的索引方式，常用方式有两种：基本切片与高级索引。本节重点讲解基本切片。

基本切片

NumPy 内置函数 slice() 可以用来构造切片对象，该函数需要传递三个参数值分别是 start（起始索引）、stop（终止索引） 和 step（步长） ，通过它可以实现从原数组的上切割出一个新数组。

示例如下：

import numpy as np
a = np.arange(10)
#生成切片对象
s = slice(2,9,3)#从索引2开始到索引9停止，间隔时间为2
print(a[s])

输出结果：

[2 5 8]

您也可以通过冒号来分割切片参数，最终也能获得相同结果，示例如下：

import numpy as np
a = np.arange(10)
b = a[2:9:2]
print(b)

输出结果：

[2 5 8]

下面对冒号切片做简单地说明：

• 如果仅输入一个参数，则将返回与索引相对应的元素。 对于上述示例来说[3]就会返回 3。
• 如果在其前面插入“:”如[:9]，则会返回 0-8 的所有数字（不包含9）。
• 如是 [2:]则会返回 2-9 之间的数字。
• 如果在两个参数之间，如[2:9]，则对两个索引值之间的所有元素进行切片（不包括停止索引）。

下面对冒号类型的切片做了简单的实例演示：

示例 1：

a = np.arange(10)
b = a[3]
print (b)

输出结果：

3

示例 2：

import numpy as np
a = np.arange(10)
print (a[2:])

输出结果:

[2 3 4 5 6 7 8 9]

示例 3：

import numpy as np
a = np.arange(10)
print a[2:5]

输出结果如下：

[2 3 4]

多维数组切片

多维数组切片操作，实例如下：

import numpy as np
a = np.array([[1,2,3],[3,4,5],[4,5,6]])
print(a)
# 从[1:]索引处开始切割
print(a[1:])

输出结果：

[[1 2 3]
 [3 4 5]
 [4 5 6]]
#切割后的新数组
[[3 4 5]
 [4 5 6]]

注意：切片还可以使用省略号“…”，如果在行位置使用省略号，那么返回值将包含所有行元素，反之，则包含所有列元素。

实例演示如下：

import numpy as np
#创建a数组
a = np.array([[1,2,3],[3,4,5],[4,5,6]])
#返回数组的第二列
print (a[...,1]) 
#返回数组的第二行
print (a[1,...])
#返回第二列后的所有项
print (a[...,1:])

输出结果：

#第二列数组
[2 4 5]
#第二行数组
[3 4 5]
#返回第二列及以后的所有元素
[[2 3]
[4 5]
[5 6]]

NumPy高级索引

NumPy 与 Python 的内置序列相比，它提供了更多的索引方式。除了在《Numpy切片和索引》一节用到索引方式外，在 NumPy 中还可以使用高级索引方式，比如整数数组索引、布尔索引以及花式索引，本节主要对上述三种索引方式做详细介绍。

高级索引返回的是数组的副本（深拷贝），而切片操作返回的是数组视图（浅拷贝）。如果您对副本和视图的概念陌生，可直接跳转学习《NumPy副本和视图》一节。

1. 整数数组索引

整数数组索引，它可以选择数组中的任意一个元素，比如，选择第几行第几列的某个元素，示例如下：

import numpy as np
#创建二维数组
x = np.array([[1,  2],  [3,  4],  [5,  6]])
#[0,1,2]代表行索引;[0,1,0]代表列索引
y = x[[0,1,2],[0,1,0]] 
print (y)

输出结果是：

[1 4 5]

对上述示例做简单分析：将行、列索引组合会得到 (0,0)、(1,1) 和 (2,0) ，它们分别对应着输出结果在原数组中的索引位置。

下面再看一组示例：获取了 4*3 数组中的四个角上元素，它们对应的行索引是 [0,0] 和 [3,3]，列索引是 [0,2] 和 [0,2]。

import numpy as np
b = np.array([[ 0, 1, 2],
              [ 3, 4, 5],
              [ 6, 7, 8],
              [ 9,10,11]])
r = np.array([[0,0],[3,3]])
c = np.array([[0,2],[0,2]])
#获取四个角的元素
c = b[r,c]
print(c)

输出结果：

[[ 0 2]
[ 9 11]]

您也可以将切片所使用的:或省略号...与整数数组索引结合使用，示例如下：

import numpy as np
d = np.array([[ 0,  1,  2],
              [ 3,  4,  5],
              [ 6,  7,  8],
              [ 9, 10, 11]])
#对行列分别进行切片
e = d[1:4,1:3]
print(e)
#行使用基础索引，对列使用高级索引
f = d[1:4,[1,2]]
#显示切片后结果
print (f)
#对行使用省略号
h=d[...,1:]
print(h)

输出结果：

#e数组
[[ 4  5]
[ 7  8]
[10 11]]
#f数组
[[ 4  5]
[ 7  8]
[10 11]]
#h数组
[[ 1,  2],
 [ 4,  5],
 [ 7,  8],
 [10, 11]]

2. 布尔数组索引

当输出的结果需要经过布尔运算（如比较运算）时，此时会使用到另一种高级索引方式，即布尔数组索引。下面示例返回数组中大于 6 的的所有元素：

#返回所有大于6的数字组成的数组
import numpy as np
x = np.array([[ 0,  1,  2],[ 3,  4,  5],[ 6,  7,  8],[ 9, 10, 11]])
print (x[x > 6])

输出结果：

[ 7 8 9 10 11]

我们可以使用补码运算符来去除 NaN（即非数字元素），如下所示：

import numpy as np
a = np.array([np.nan, 1,2,np.nan,3,4,5])
print(a[~np.isnan(a))

输出结果：

[ 1. 2. 3. 4. 5.]

下面示例，删除数组中整数元素，如下所示：

import numpy as np
a = np.array([1, 2+6j, 5, 3.5+5j])
print( a[np.iscomplex(a)])

输出结果如下：

[2.0+6.j 3.5+5.j]

3. 花式索引（拓展知识）

花式索引也可以理解为整数数组索引，但是它们之间又略有不同，下面通过示例做简单讲解。（本内容作为拓展知识了解即可）

花式索引也会生成一个新的副本。

当原数组是一维数组时，使用一维整型数组作为索引，那么索引结果就是相应索引位置上的元素。

>>> import numpy as np
>>> x=np.array([1,2,3,4])
>>> print(x[0])
1

如果原数组是二维数组，那么索引数组也需要是二维的，索引数组的元素值与被索引数组的每一行相对应，示例如下：

import numpy as np
x=np.arange(32).reshape((8,4))
#分别对应 第4行数据、第2行数据、第1行数据、第7行数据项
print (x[[4,2,1,7]])

输出结果：

[[16 17 18 19]
[ 8  9 10 11]
[ 4  5  6  7]
[28 29 30 31]]

也可以使用倒序索引数组，示例如下：

import numpy as np
x=np.arange(32).reshape((8,4))
print (x[[-4,-2,-1,-7]])

输出结果：

[[16 17 18 19]
[24 25 26 27]
[28 29 30 31]
[ 4  5  6  7]]

还可以同时使用多个索引数组，但这种情况下需要添加np.ix_。

import numpy as np
x=np.arange(32).reshape((8,4))
print (x[np.ix_([1,5,7,2],[0,3,1,2])])

输出结果如下：

[[ 4  7  5  6]
[20 23 21 22]
[28 31 29 30]
[ 8 11  9 10]]

其中 [1,5,7,2] 代表行索引，而 [0,3,1,2] 表示与行索引相对应的列索引值，也就是行中的元素值会按照列索引值排序。比如，第一行元素，未排序前的顺序是 [4,5,6,7]，经过列索引排序后变成了 [4,7,5,6]。

NumPy广播机制

NumPy 中的广播机制（Broadcast）旨在解决不同形状数组之间的算术运算问题。我们知道，如果进行运算的两个数组形状完全相同，它们直接可以做相应的运算。示例如下：

import numpy as np
a = np.array([0.1,0.2,0.3,0.4])
b = np.array([10,20,30,40])
c = a * b
print(c)

输出结果如下：

[ 1. 4. 9. 16.]

但如果两个形状不同的数组呢？它们之间就不能做算术运算了吗？当然不是！为了保持数组形状相同，NumPy 设计了一种广播机制，这种机制的核心是对形状较小的数组，在横向或纵向上进行一定次数的重复，使其与形状较大的数组拥有相同的维度。

当进行运算的两个数组形状不同，Numpy 会自动触发广播机制。示例如下：

import numpy as np
a = np.array([[ 0, 0, 0],
           [10,10,10],
           [20,20,20],
           [30,30,30]])
#b数组与a数组形状不同
b = np.array([1,2,3])
print(a + b)

输出结果为：

[[ 1  2  3]
[11 12 13]
[21 22 23]
[31 32 33]]

下图 1 ：通过数组 a 、b 的运算展示了广播机制的实现流程。

图1：Numpy 数组广播机制

4x3 的二维 a 数组 与 1x3 的一维 b 数组相加，本质上可以理解为 b 数组在纵向上向下拓展 3 次（将第一行重复 3 次），从而生成与 a 数组相同形状的数组，之后再与 a 数组进行运算。

NumPy遍历数组

NumPy 提供了一个 nditer 迭代器对象，它可以配合 for 循环完成对数组元素的遍历。

下面看一组示例，使用 arange() 函数创建一个 3*4 数组，并使用 nditer 生成迭代器对象。

示例1：

import numpy as npa = np.arange(0,60,5)a = a.reshape(3,4)#使用nditer迭代器,并使用for进行遍历for x in np.nditer(a):   print(x)

输出结果：

0 5 10 15 20 25 30 35 40 45 50 55

遍历顺序

在内存中，Numpy 数组提供了两种存储数据的方式，分别是 C-order（行优先顺序）与 Fortrant-order（列优先顺序）。那么 nditer 迭代器又是如何处理具有特定存储顺序的数组呢？其实它选择了一种与数组内存布局一致的顺序，之所以这样做，是为了提升数据的访问效率。

在默认情况下，当我们遍历数组中元素的时候，不需要考虑数组的存储顺序，这一点可以通过遍历上述数组的转置数组来验证。

示例 2：

import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)
#a的转置数组
b = a.T
print (b)
for x in np.nditer(b):
   print(x，end=",")

输出结果：

#转置数组b
[[ 0 20 40]
[ 5 25 45]
[10 30 50]
[15 35 55]]

#a转置后的遍历输出
0 5 10 15 20 25 30 35 40 45 50 55

从示例 1、2 的输出结果可以看出，a 和 a.T 的遍历顺序是一样的，也就是说，它们在内存中的存储顺序是一样的。

下面以 C 样式访问转置数组的副本。示例 3 如下：

import numpy as np
a = np.arange(0,60,5).reshape(3,4)
#copy方法生成数组副本
for x in np.nditer(a.T.copy(order='C')):
    print (x, end=", " )

输出结果：

0, 20, 40, 5, 25, 45, 10, 30, 50, 15, 35, 55,

通过示例 3 可知 a.T.copy(order = ‘C’) 的遍历结果与示例 1、2 的数组遍历结果不一样。究其原因，就是因为它们在内存中的存储方式不一样。

指定遍历顺序

您可以通过 nditer 对象的order参数来指定数组的遍历的顺序。示例 4 如下：

import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)
print(a)
for x in np.nditer(a, order = 'C'):
   print (x,end=",") 
for x in np.nditer(a, order = 'F'):
   print (x,end=",")

输出结果如下：

#c=order行顺序
0,5,10,15,20,25,30,35,40,45,50,55,
#F-order列顺序
0,20,40,5,25,45,10,30,50,15,35,55,

修改数组元素值

nditer 对象提供了一个可选参数op_flags，它表示能否在遍历数组时对元素进行修改。它提供了三种模式，如下所示：

1) read-only

只读模式，在这种模式下，遍历时不能修改数组中的元素。

2) read-write

读写模式，遍历时可以修改元素值。

3) write-only

只写模式，在遍历时可以修改元素值。

示例如下：

import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4) 
print ("原数组是:",a)
for x in np.nditer(a, op_flags=['readwrite']):
    x[...]=2*x
print ('修改后的数组是：',a)

最后输出结果如下：

原数组是:
[[ 0  5 10 15]
[20 25 30 35]
[40 45 50 55]]
修改后的数组是： 
[[ 0  10  20  30]
[ 40  50  60  70]
[ 80  90 100 110]]

外部循环使用

nditer 对象的构造函数有一个“flags”参数，它可以接受以下参数值（了解即可）：

参数值	描述说明
c_index	可以跟踪 C 顺序的索引。
f_index	可以跟踪 Fortran 顺序的索引。
multi_index	每次迭代都会跟踪一种索引类型。
external_loop	返回的遍历结果是具有多个值的一维数组。

示例 6 如下：

import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)
print("原数组",a)
#修改后数组
for x in np.nditer(a, flags = ['external_loop'], order = 'F'):
   print(x)

结果输出：

原数组: 
[[ 0  5 10 15]
[20 25 30 35]
[40 45 50 55]]
#修改后的一维数组
[ 0 20 40]
[ 5 25 45]
[10 30 50]
[15 35 55]

迭代多个数组

如果两个数组都能够被广播，那么 nditer 对象就可以同时对它们迭代。

假设数组 a 的维度是 34，另一个数组 b 的维度是 14 （即维度较小的数组 b 可以被广播到数组 a 中），示例如下：

import numpy as np
a = np.arange(0,60,5)
a = a.reshape(3,4)
print (a)
b = np.array([1, 2, 3, 4], dtype = int)
print (b） 
#广播迭代
for x,y in np.nditer([a,b]):
    print ("%d:%d" % (x,y),end=",")

输出结果是：

0:1,5:2,10:3,15:4,20:1,25:2,30:3,35:4,40:1,45:2,50:3,55:4,

NumPy相关数组操作

NumPy 中包含了一些处理数组的常用方法，大致可分为以下几类：

• 数组变维操作
• 数组转置操作
• 修改数组维度操作
• 连接与分割数组操作

下面分别对它们进行介绍。

数组变维操作

函数名称	函数介绍
reshape	在不改变数组元素的条件下，修改数组的形状。
flat	返回是一个迭代器，可以用 for 循环遍历其中的每一个元素。
flatten	以一维数组的形式返回一份数组的副本，对副本的操作不会影响到原数组。
ravel	返回一个连续的扁平数组（即展开的一维数组），与 flatten不同，它返回的是数组视图（修改视图会影响原数组）。

reshape 在《NumPy ndarray对象》一节已经做了讲解，本节不再介绍。

1) numpy.ndarray.flat

numpy.ndarray.flat 返回一个数组迭代器，实例如下:

import numpy as np
a = np.arange(9).reshape(3,3)
for row in a:
    print (row)
#使用flat属性：
for ele in a.flat:
    print (ele,end="，")

输出结果如下：

#原数组
[0 1 2]
[3 4 5]
[6 7 8]
#输出元素
0，1，2，3，4，5，6，7，8，

2) numpy.ndarray.flatten()

numpy.ndarray.flatten 返回一份数组副本，对副本修改不会影响原始数组，其语法格式如下：

ndarray.flatten(order=‘C’)

实例如下：

import numpy as np
a = np.arange(8).reshape(2,4)
print (a)
#默认按行C风格展开的数组
print (a.flatten())
#以F风格顺序展开的数组
print (a.flatten(order = 'F'))

输出结果：

#数组a
[[0 1 2 3]
[4 5 6 7]]
#默认c顺序站看数组
[0 1 2 3 4 5 6 7]
# F顺序站看数组
[0 4 1 5 2 6 3 7]

3) numpy.ravel()

numpy.ravel() 将多维数组中的元素以一维数组的形式展开，该方法返回数组的视图（view），如果修改，则会影响原始数组。

numpy.ravel(a, order=‘C’)

实例结果如下：

import numpy as np
a = np.arange(8).reshape(2,4)
print ('原数组：')
print (a)
print ('调用 ravel 函数后：')
print (a.ravel())
print ('F 风格顺序调用 ravel 函数之后：')
print (a.ravel(order = 'F'))

输出结果如下：

原数组：
[[0 1 2 3]
[4 5 6 7]]
调用 ravel 函数后：
[0 1 2 3 4 5 6 7]
F 风格顺序调用 ravel 函数之后：
[0 4 1 5 2 6 3 7]

数组转置操作

函数名称	说明
transpose	将数组的维度值进行对换，比如二维数组维度(2,4)使用该方法后为(4,2)。
ndarray.T	与 transpose 方法相同。
rollaxis	沿着指定的轴向后滚动至规定的位置。
swapaxes	对数组的轴进行对换。

1) numpy.transpose()

numpy.transpose() 用于对换多维数组的维度，比如二维数组使用此方法可以实现矩阵转置，语法格式如下：

numpy.transpose(arr, axes)

参数说明如下：

• arr：要操作的数组
• axes：可选参数，元组或者整数列表，将会按照该参数进行转置。

示例如下：

import numpy as np
a = np.arange(12).reshape(3,4)
print (a)
print (np.transpose(a))

输出结果：

原数组：
[[ 0  1  2  3]
[ 4  5  6  7]
[ 8  9 10 11]]

对换数组：
[[ 0  4  8]
[ 1  5  9]
[ 2  6 10]
[ 3  7 11]]

ndarray.T 的使用方法与其类似，这里就在赘述。

2) numpy.rollaxis()

该方法表示沿着指定的轴，向后滚动至一个特定位置，格式如下：

numpy.rollaxis(arr, axis, start)

参数说明：

• arr：要传入的数组；
• axis：沿着哪条轴向后滚动，其它轴的相对位置不会改变；
• start：默认以 0 轴开始，可以根据数组维度调整它的值。

3) numpy.swapaxes()

该方法用于交换数组的两个轴，其语法格式如下：

numpy.swapaxes(arr, axis1, axis2)

示例如：

import numpy as np
# 创建了三维的 ndarray
a = np.arange(27).reshape(3,3,3)
print (a)
#对换0轴与2轴
print(np.swapaxes(a,2,0))

输出结果：

#原a数组
[[[ 0  1  2]
  [ 3  4  5]
  [ 6  7  8]]

[[ 9 10 11]
  [12 13 14]
  [15 16 17]]

[[18 19 20]
  [21 22 23]
  [24 25 26]]]
#对换轴后的数组
[[[ 0  9 18]
  [ 3 12 21]
  [ 6 15 24]]

[[ 1 10 19]
  [ 4 13 22]
  [ 7 16 25]]

[[ 2 11 20]
  [ 5 14 23]
  [ 8 17 26]]]

修改数组维度操作

修改数组维度的操作，主要有以下方法：

函数名称	描述说明
broadcast	生成一个模拟广播的对象。
broadcast_to	将数组广播为新的形状。
expand_dims	扩展数组的形状。
squeeze	从数组的形状中删除一维项。

1) numpy.broadcast()

返回值是数组被广播后的对象，该函数以两个数组作为输入参数，实例如下：

import numpy as np
a = np.array([[1], [2], [3]])
b = np.array([4, 5, 6]) 
# 对b广播a
d = np.broadcast(a,b) 
#d它拥有 iterator 属性
r,c = d.iters
print (next(r), next(c))
print (next(r), next(c))
# 使用broadcast将a与b相加
e = np.broadcast(a,b)
f=np.empty(e.shape)
f.flat=[x+y for (x,y) in e]
print(f)
print(a+b)

输出结果：

#对b广播a
1 6
2 4
#f数组
[[5. 6. 7.]
[6. 7. 8.]
[7. 8. 9.]]
#a+b
[[5 6 7]
[6 7 8]
[7 8 9]]

2) numpy.broadcast_to()

该函数将数组广播到新形状中，它在原始数组的基础上返回一个只读视图。 如果新形状不符合 NumPy 的广播规则，则会抛出 ValueError 异常。函数的语法格式如下：

numpy.broadcast_to(array, shape, subok)

使用实例如下所示：

import numpy as np
a = np.arange(4).reshape(1,4)
print("原数组",a)
print ('调用 broadcast_to 函数之后：')
print (np.broadcast_to(a,(4,4)))

最后的输出结果如下：

#原数组
[[0 1 2 3]]

#调用 broadcast_to 函数之后：
[[0 1 2 3]
[0 1 2 3]
[0 1 2 3]
[0 1 2 3]]

3) numpy.expand_dims()

在指定位置插入新的轴，从而扩展数组的维度，语法格式如下:

numpy.expand_dims(arr, axis)

参数说明：

• arr：输入数组
• axis：新轴插入的位置

实例如下：

import numpy as np
x = np.array(([1,2],[3,4]))
print ('数组 x：')
print (x)
# 在 0 轴处插入新的轴
y = np.expand_dims(x, axis = 0)
print ('数组 y：')
print (y)
print ('\n')
print ('数组 x 和 y 的形状：')
print (x.shape, y.shape)

输出结果为：

数组 x：
[[1 2]
[3 4]]

数组 y：
[[[1 2]
  [3 4]]]

数组 x 和 y 的形状：
(2, 2) (1, 2, 2)

4) numpy.squeeze()

删除数组中维度为 1 的项，例如，一个数组的 shape 是 (5,1)，经此函数后，shape 变为 (5,) 。其函数语法格式如下：

numpy.squeeze(arr, axis)

参数说明：

• arr：输入数的组；
• axis：取值为整数或整数元组，用于指定需要删除的维度所在轴，指定的维度值必须为 1 ，否则将会报错，若为 None，则删除数组维度中所有为 1 的项。

下面是带有 axis 参数的实例：

>>> x = np.array([[[0], [1], [2]]])
>>> x.shape
(1, 3, 1)
>>> np.squeeze(x).shape
(3,)
>>> np.squeeze(x, axis=(2,)).shape
(1, 3)

再看另一组示例，如下所示：

import numpy as np
a = np.arange(9).reshape(1,3,3)
print (a)
b = np.squeeze(a)
print (b)
print ('数组 a 和 b 的形状：')
print (x.shape, y.shape)

输出结果为：

数组 a:
[[[0 1 2]
  [3 4 5]
  [6 7 8]]]

数组 b：
[[0 1 2]
[3 4 5]
[6 7 8]]

数组 a 和 b 的形状：
(1, 3, 3) (3, 3)

连接与分割数组操作

连接与分割数组是数组的两种操作方式，我们为了便于大家记忆，现将它们的方法整合在一起，如下所示：

类型	函数名称	描述说明
连接数组方法	concatenate	沿指定轴连接两个或者多个相同形状的数组
stack	沿着新的轴连接一系列数组
hstack	按水平顺序堆叠序列中数组（列方向）
vstack	按垂直方向堆叠序列中数组（行方向）
分割数组方法	split	将一个数组分割为多个子数组
hsplit	将一个数组水平分割为多个子数组（按列）
vsplit	将一个数组垂直分割为多个子数组（按行）

1) 连接数组操作

numpy.concatenate() 沿指定轴连接相同形状的两个或多个数组，格式如下：

numpy.concatenate((a1, a2, …), axis)

参数说明：

• a1, a2, …：表示一系列相同类型的数组；
• axis：沿着该参数指定的轴连接数组，默认为 0。

实例说明：创建两个 a 、b 数组，并沿指定轴将它们连接起来。注意两个数组的形状要保持一致。

import numpy as np
#创建数组a
a = np.array([[10,20],[30,40]])
print (a)
#创建数组b
b = np.array([[50,60],[70,80]])
print (b)
#沿轴 0 连接两个数组
print (np.concatenate((a,b)))
#沿轴 1 连接两个数组
print (np.concatenate((a,b),axis = 1))

输出结果：

#a
[[10 20]
[30 40]]
#b
[[50 60]
[70 80]]
#axis=0沿着垂直方向
[[10 20]
[30 40]
[50 60]
[70 80]]
#axis=1沿着水平方向
[[10 20 50 60]
[30 40 70 80]]

数组连接操作至少需要两个维度相同的数组，才允许对它们进行垂直或者水平方向上的操作。

在垂直方向堆叠数组，示例如下：

import numpy as np
a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])
#垂直堆叠
c = np.vstack((a,b))
print (c)

输出结果如下：

[[1 2]
[3 4]
[5 6]
[7 8]]

2) 分割数组操作

numpy.split() 沿指定的轴将数组分割为多个子数组，语法格式如下：

numpy.split(ary, indices_or_sections, axis)

参数说明：

• ary：被分割的数组
• indices_or_sections：若是一个整数，代表用该整数平均切分，若是一个数组，则代表沿轴切分的位置（左开右闭）；
• axis：默认为0，表示横向切分；为1时表示纵向切分。

示例如下所示：

import numpy as np
a = np.arange(6)
#原数组
print (a)
#将数组分为二个形状大小相等的子数组
b = np.split(a,2)
print (b)
#将数组在一维数组中标明要位置分割
b = np.split(a,[3,4])
print (b)

输出结果如下：

#a数组
[0 1 2 3 4 5]
#切分分形状大小相同的数组
[array([0, 1, 2]), array([3, 4, 5])]
#按数组标明位置切分,切分时左开右闭
[array([0, 1, 2]), array([3]), array([4, 5])]

最后看一下 hsplit() 的使用方法，示例如下：

import numpy as np
#arr1数组
arr1 = np.floor(10 * np.random.random((2, 6)))
print(arr1)
#拆分后数组
print(np.hsplit(arr1, 3))

输出结果：

#原arr1数组
[[2. 1. 5. 3. 1. 7.]
 [1. 2. 9. 0. 9. 9.]]
#经过水平切分后得到的数组
[array([[2., 1.],
       [1., 2.]]), array([[5., 3.],
       [9., 0.]]), array([[1., 7.],
       [9., 9.]])]]

NumPy数组元素增删改查

本节重点介绍 NumPy 数组元素的增删改查操作，主要有以下方法：

函数名称	描述说明
resize	返回指定形状的新数组。
append	将元素值添加到数组的末尾。
insert	沿规定的轴将元素值插入到指定的元素前。
delete	删掉某个轴上的子数组，并返回删除后的新数组。
argwhere	返回数组内符合条件的元素的索引值。
unique	用于删除数组中重复的元素，并按元素值由大到小返回一个新数组。

1. numpy.resize()

numpy.resize() 返回指定形状的新数组。

numpy.resize(arr, shape)

使用示例：

import numpy as np
a = np.array([[1,2,3],[4,5,6]])
print(a)
#a数组的形状
print(a.shape)
b = np.resize(a,(3,2))
#b数组
print (b)
#b数组的形状
print(b.shape)
#修改b数组使其形状大于原始数组
b = np.resize(a,(3,3))
print(b)

输出结果为：

a数组：
[[1 2 3]
[4 5 6]]

a形状：
(2, 3)

b数组：
[[1 2]
[3 4]
[5 6]]

b数组的形状：
(3, 2)

修改后b数组：
[[1 2 3]
[4 5 6]
[1 2 3]]

这里需要区别 resize() 和 reshape() 的使用方法，它们看起来相似，实则不同。resize 仅对原数组进行修改，没有返回值，而 reshape 不仅对原数组进行修改，同时返回修改后的结果。

看一组示例，如下所示：

In [1]: import numpy as np
In [2]: x=np.arange(12)
#调用resize方法
In [3]: x_resize=x.resize(2,3,2)
In [4]: x
Out[4]:
array([[[ 0,  1],
        [ 2,  3],
        [ 4,  5]],
       [[ 6,  7],
        [ 8,  9],
        [10, 11]]])
In [5]: x_resize
#返回None使用print打印
In [6]: print(x_resize)
None
#调用reshape方法
In [7]: x_shape=x.reshape(2,3,2)
#返回修改后的数组
In [8]: x_shape
Out[8]:
array([[[ 0,  1],
        [ 2,  3],
        [ 4,  5]],
       [[ 6,  7],
        [ 8,  9],
        [10, 11]]])
In [9]: x
Out[9]:
array([[[ 0,  1],
        [ 2,  3],
        [ 4,  5]],
       [[ 6,  7],
        [ 8,  9],
        [10, 11]]])

2. numpy.append()

在数组的末尾添加值，它返回一个一维数组。

numpy.append(arr, values, axis=None)

参数说明：

• arr：输入的数组；
• values：向 arr 数组中添加的值，需要和 arr 数组的形状保持一致；
• axis：默认为 None，返回的是一维数组；当 axis =0 时，追加的值会被添加到行，而列数保持不变，若 axis=1 则与其恰好相反。

使用示例：

import numpy as np
a = np.array([[1,2,3],[4,5,6]])
#向数组a添加元素
print (np.append(a, [7,8,9]))
#沿轴 0 添加元素
print (np.append(a, [[7,8,9]],axis = 0))
#沿轴 1 添加元素
print (np.append(a, [[5,5,5],[7,8,9]],axis = 1))

输出结果为：

向数组a添加元素：
[1 2 3 4 5 6 7 8 9]

沿轴 0 添加元素：
[[1 2 3]
[4 5 6]
[7 8 9]]

沿轴 1 添加元素：
[[1 2 3 5 5 5]
[4 5 6 7 8 9]]

3. numpy.insert()

表示沿指定的轴，在给定索引值的前一个位置插入相应的值，如果没有提供轴，则输入数组被展开为一维数组。

numpy.insert(arr, obj, values, axis)

参数说明：

• arr：要输入的数组
• obj：表示索引值，在该索引值之前插入 values 值；
• values：要插入的值；
• axis：指定的轴，如果未提供，则输入数组会被展开为一维数组。

示例如下：

import numpy as np
a = np.array([[1,2],[3,4],[5,6]])
#不提供axis的情况，会将数组展开
print (np.insert(a,3,[11,12]))
#沿轴 0 垂直方向
print (np.insert(a,1,[11],axis = 0))
#沿轴 1 水平方向
print (np.insert(a,1,11,axis = 1))

输出结果如下：

提供 axis 参数：
[ 1  2  3 11 12  4  5  6]

沿轴 0：
[[ 1  2]
[11 11]
[ 3  4]
[ 5  6]]

沿轴 1：
[[ 1 11  2]
[ 3 11  4]
[ 5 11  6]]

4. numpy.delete()

该方法表示从输入数组中删除指定的子数组，并返回一个新数组。它与 insert() 函数相似，若不提供 axis 参数，则输入数组被展开为一维数组。

numpy.delete(arr, obj, axis)

参数说明：

• arr：要输入的数组；
• obj：整数或者整数数组，表示要被删除数组元素或者子数组；
• axis：沿着哪条轴删除子数组。

使用示例：

import numpy as np
a = np.arange(12).reshape(3,4)
#a数组
print(a)
#不提供axis参数情况
print(np.delete(a,5))
#删除第二列
print(np.delete(a,1,axis = 1))
#删除经切片后的数组
a = np.array([1,2,3,4,5,6,7,8,9,10])
print (np.delete(a, np.s_[::2]))

输出结果为：

a数组：
[[ 0  1  2  3]
[ 4  5  6  7]
[ 8  9 10 11]]

无 axis 参数：
[ 0  1  2  3  4  6  7  8  9 10 11]

删除第二列：
[[ 0  2  3]
[ 4  6  7]
[ 8 10 11]]

删除经过切片的数组：
[ 2  4  6  8 10]

5. numpy.argwhere()

该函数返回数组中非 0 元素的索引，若是多维数组则返回行、列索引组成的索引坐标。

示例如下所示：

import numpy as np
x = np.arange(6).reshape(2,3)
print(x)
#返回所有大于1的元素索引
y=np.argwhere(x>1)
print(y)

输出结果：

#x数组
[[0 1 2]
[3 4 5]]
#返回行列索引坐标
[[0 2]
[1 0]
[1 1]
[1 2]]

6. numpy.unique()

用于删除数组中重复的元素，其语法格式如下：

numpy.unique(arr, return_index, return_inverse, return_counts)

参数说明：

• arr：输入数组，若是多维数组则以一维数组形式展开；
• return_index：如果为 True，则返回新数组元素在原数组中的位置（索引）；
• return_inverse：如果为 True，则返回原数组元素在新数组中的位置（索引）；
• return_counts：如果为 True，则返回去重后的数组元素在原数组中出现的次数。

示例如下：

import numpy as np
a = np.array([5,2,6,2,7,5,6,8,2,9])
print (a)
#对a数组的去重
uq = np.unique(a)
print (uq)
#数组去重后的索引数组
u,indices = np.unique(a, return_index = True)
#打印去重后数组的索引
print(indices)
#去重数组的下标：
ui,indices = np.unique(a,return_inverse = True)
print (ui)
#打印下标
print (indices)
#返回去重元素的重复数量
uc,indices = np.unique(a,return_counts = True)
print (uc)
元素出现次数：
print (indices)

输出结果为：

a数组：
[5 2 6 2 7 5 6 8 2 9]

去重后的a数组
[2 5 6 7 8 9]

去重数组的索引数组：
[1 0 2 4 7 9]

去重数组的下标：
[2 5 6 7 8 9]

原数组在新数组中的下标：
[1 0 2 0 3 1 2 4 0 5]

返回去重元素的重复数量：
[2 5 6 7 8 9]

统计重复元素出现次数：
[3 2 2 1 1 1]

NumPy数学函数

NumPy 中包含了大量的数学函数，它们用于执行各种数学运算，其中包括三角函数、舍入函数等等。下面对它们做详细讲解。

三角函数

NumPy 中提供了用于弧度计算的的 sin()（正弦）、cos()（余弦）和 tan()（正切）三角函数。

示例如下：

import numpy as np 
arr = np.array([0, 30, 60, 90, 120, 150, 180]) 
#计算arr数组中给定角度的三角函数值
#通过乘以np.pi/180将其转换为弧度
print(np.sin(arr * np.pi/180)) 
print(np.cos(arr * np.pi/180)) 
print(np.tan(arr * np.pi/180))  

输出结果如下：

sin()正弦值:
[0.00000000e+00 5.00000000e-01 8.66025404e-01 1.00000000e+00
8.66025404e-01 5.00000000e-01 1.22464680e-16]
cos()余弦值：
[ 1.00000000e+00  8.66025404e-01  5.00000000e-01  6.12323400e-17
-5.00000000e-01 -8.66025404e-01 -1.00000000e+00]
tan()正切值：
[ 0.00000000e+00  5.77350269e-01  1.73205081e+00  1.63312394e+16
-1.73205081e+00 -5.77350269e-01 -1.22464680e-16]

除了上述三角函数以外，NumPy 还提供了 arcsin，arcos 和 arctan 反三角函数。

若要想验证反三角函数的结果，可以通过 numpy.degrees() 将弧度转换为角度来实现，示例如下：

import numpy as np 
arr = np.array([0, 30, 60, 90]) 
#正弦值数组
sinval = np.sin(arr*np.pi/180) 
print(sinval) 
#计算角度反正弦，返回值以弧度为单位
cosec = np.arcsin(sinval) 
print(cosec) 
#通过degrees函数转化为角度进行验证
print(np.degrees(cosec)) 
#余弦值数组
cosval = np.cos(arr*np.pi/180) 
print(cosval) 
#计算反余弦值，以弧度为单位
sec = np.arccos(cosval) 
print(sec) 
#通过degrees函数转化为角度进行验证
print(np.degrees(sec)) 
#下面是tan()正切函数 
tanval = np.tan(arr*np.pi/180) 
print(tanval) 
cot = np.arctan(tanval) 
print(cot) 
print(np.degrees(cot))  

输出结果：

正选值数组：
[0.        0.5       0.8660254 1.       ]
#计算角度反正弦值，以弧度为单位
[0.         0.52359878 1.04719755 1.57079633]
通过degrees验证
[ 0. 30. 60. 90.]
余弦数组：
[1.00000000e+00 8.66025404e-01 5.00000000e-01 6.12323400e-17]
通过degrees验证
[0.         0.52359878 1.04719755 1.57079633]
反余弦值：
[ 0. 30. 60. 90.]

正切数组：
[0.00000000e+00 5.77350269e-01 1.73205081e+00 1.63312394e+16]
反正切值：
[0.         0.52359878 1.04719755 1.57079633]
通过degrees验证
[ 0. 30. 60. 90.]

舍入函数

NumPy 提供了三个舍入函数，介绍如下：

1) numpy.around()

该函数返回一个十进制值数，并将数值四舍五入到指定的小数位上。该函数的语法如下：

numpy.around(a,decimals)

参数说明：

• a：代表要输入的数组；
• decimals：要舍入到的小数位数。它的默认值为0，如果为负数，则小数点将移到整数左侧。

示例如下：

import numpy as np 
arr = np.array([12.202, 90.23120, 123.020, 23.202]) 
print(arr) 
print("数组值四舍五入到小数点后两位",np.around(arr, 2)) 
print("数组值四舍五入到小数点后-1位",np.around(arr, -1))  

输出结果：

原数组arr：[12.202 90.2312 123.02 23.202]
数组值四舍五入到小数点后两位[12.2 90.23 123.02 23.2]
数组值四舍五入到小数点后-1位[10. 90. 120. 20.]

2) numpy.floor()

该函数表示对数组中的每个元素向下取整数，即返回不大于数组中每个元素值的最大整数。示例如下：

import numpy as np
a = np.array([-1.8,  1.1,  -0.4,  0.9,  18])
#对数组a向下取整
print (np.floor(a))

输出结果：

[-2. 1. -1. 0. 18.]

3) numpy.ceil()

该函数与 floor 函数相反，表示向上取整。示例如下：

import numpy as np
a = np.array([-1.8,  1.1,  -0.4,  0.9,  18])
#对数组a向上取整
print (np.ceil(a))

输出结果：

[-1. 2. -0. 1. 18.]

NumPy算术运算

NumPy 数组的“加减乘除”算术运算，分别对应 add()、subtract()、multiple() 以及 divide() 函数。

注意：做算术运算时，输入数组必须具有相同的形状，或者符合数组的广播规则，才可以执行运算。

下面看一组示例：

import numpy as np
a = np.arange(9, dtype = np.float_).reshape(3,3)
#数组a
print(a)
#数组b
b = np.array([10,10,10])
print(b)
#数组加法运算
print(np.add(a,b))
#数组减法运算
print(np.subtract(a,b))
#数组乘法运算
print(np.multiply(a,b))
#数组除法运算
print(np.divide(a,b))

输出结果：

a数组:
[[ 0. 1. 2.]
[ 3. 4. 5.]
[ 6. 7. 8.]]
b数组：
[10 10 10]
加：
[[ 10. 11. 12.]
[ 13. 14. 15.]
[ 16. 17. 18.]]
减：
[[-10. -9. -8.]
[ -7. -6. -5.]
[ -4. -3. -2.]]

乘：
[[ 0. 10. 20.]
[ 30. 40. 50.]
[ 60. 70. 80.]]
除：
[[ 0. 0.1 0.2]
[ 0.3 0.4 0.5]
[ 0.6 0.7 0.8]]

下面介绍了 NumPy 中其他重要的算术运算函数。

numpy.reciprocal()

该函数对数组中的每个元素取倒数，并以数组的形式将它们返回。

当数组元素的数据类型为整型（int）时，对于绝对值小于 1 的元素，返回值为 0，而当数组中包含 0 元素时，返回值将出现 overflow（inf） 溢出提示，示例如下：

import numpy as np
#注意此处有0
a = np.array([0.25, 1.33, 1, 0, 100])
#数组a默认为浮点类型数据
print(a)
#对数组a使用求倒数操作
print (np.reciprocal(a))
#b数组的数据类型为整形int
b = np.array([100], dtype = int)
print(b)
#对数组b使用求倒数操作
print( np.reciprocal(b) )

输出结果：

a数组：
[   0.25    1.33    1.      0.    100.  ]

对a数组求倒数有inf提示：
__main__:1: RuntimeWarning: divide by zero encountered in reciprocal
[ 4.         0.7518797  1.               inf  0.01     ]

b数组：
[100]

对b数组求倒数：
[0]

numpy.power()

该函数将 a 数组中的元素作为底数，把 b 数组中与 a 相对应的元素作幂 ，最后以数组形式返回两者的计算结果。示例如下：

import numpy as np
a = np.array([10,100,1000]) 
#a数组
print ('我们的数组是；')
#调用 power 函数
print (np.power(a,2))
b数组
b = np.array([1,2,3]) 
print (b)
调用 power 函数
print (np.power(a,b))

输出结果：

a数组是:
[  10  100 1000]

调用 power 函数：
[    100   10000 1000000]

b数组：
[1 2 3]

调用 power 函数：
[        10      10000 1000000000]

numpy.mod()

返回两个数组相对应位置上元素相除后的余数，它与 numpy.remainder() 的作用相同 。

import numpy as np
a = np.array([11,22,33])
b = np.array([3,5,7])
#a与b相应位置的元素做除法
print( np.mod(a,b))
#remainder方法一样
print(np.remainder(a,b)) 

输出结果：

mod：                                          
[1 0 2]
remainder：                            
[1 0 2]

复数数组处理函数

NumPy 提供了诸多处理复数类型数组的函数，主要有以下几个：

• numpy.real() 返回复数数组的实部；
• numpy.imag() 返回复数数组的虚部；
• numpy.conj() 通过更改虚部的符号，从而返回共轭复数；
• numpy.angle() 返回复数参数的角度，该函数的提供了一个 deg 参数，如果 deg=True，则返回的值会以角度制来表示，否则以以弧度制来表示。

示例如下所示：

import numpy as np
a = np.array([-5.6j, 0.2j, 11. , 1+1j])
print(a)
#real() 
print np.real(a)
#imag() 
print np.imag(a)
#conj()
print np.conj(a)
#angle() 
print np.angle(a)
#angle() 带参数deg
print np.angle(a, deg = True)

输出结果：

a数组：
[ 0.-5.6j 0.+0.2j 11.+0.j 1.+1.j ]

real():
[ 0. 0. 11. 1.]

imag():
[-5.6 0.2 0. 1. ]

conj():
[ 0.+5.6j 0.-0.2j 11.-0.j 1.-1.j ]

angle() :
[-1.57079633 1.57079633 0. 0.78539816]

angle(a,deg=True)
[-90. 90. 0. 45.]

NumPy统计函数

NumPy 提供了许多统计功能的函数，比如查找数组元素的最值、百分位数、方差以及标准差等。

numpy.amin() 和 numpy.amax()

这两个函数用于计算数组沿指定轴的最小值与最大值：

• amin() 沿指定的轴，查找数组中元素的最小值，并以数组形式返回；
• amax() 沿指定的轴，查找数组中元素的最大值，并以数组形式返回。

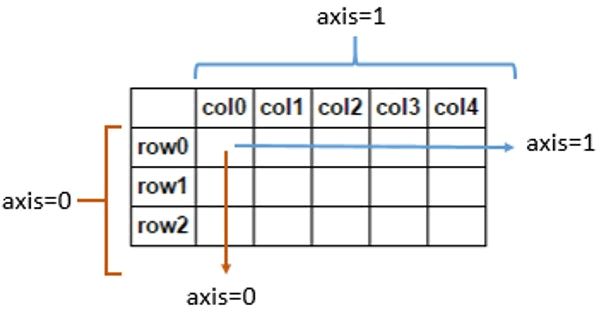
对于二维数组来说，axis=1 表示沿着水平方向，axis=0 表示沿着垂直方向。

图1：axis轴

示例如下：

import numpy as np
a = np.array([[3,7,5],[8,4,3],[2,4,9]]) 
print ('数组a是：')
print(a)
#amin()函数
print (np.amin(a))
#调用 amin() 函数，axis=1
print(np.amin(a,1))
#调用amax()函数
print(np.amax(a))
#再次调用amax()函数
print(np.amax(a,axis=0))

输出结果如下所示：

我们的数组是：
[[3 7 5]
[8 4 3]
[2 4 9]]

调用amin()函数：
2

调用 amin(axis=1) 函数：
[3 3 2]

amax() 函数：
9
amax(axis=0) 函数：
[8 7 9]

numpy.ptp()

numpy.ptp() 用于计算数组元素中最值之差值，也就是（最大值 - 最小值）。

import numpy as np 
a = np.array([[2,10,20],[80,43,31],[22,43,10]]) 
print("原数组",a) 
print("沿着axis 1:",np.ptp(a,1)) 
print("沿着axis 0:",np.ptp(a,0)) 

输出结果：

原数组 array:
[[ 2 10 20]
[80 43 31]
[22 43 10]]

沿着 axis 1: [18 49 33]
沿着 axis 0: [78 33 21]

numpy.percentile()

百分位数，是统计学中使用的一种度量单位。该函数表示沿指定轴，计算数组中任意百分比分位数，语法格式如下：

numpy.percentile(a, q, axis)

函数 numpy.percentile() 的参数说明：

• a：输入数组；
• q：要计算的百分位数，在 0~100 之间；
• axis：沿着指定的轴计算百分位数。

示例如下：

import numpy as np 
a = np.array([[2,10,20],[80,43,31],[22,43,10]]) 
print("数组a:",a) 
print("沿着axis=0计算百分位数",np.percentile(a,10,0)) 
print("沿着axis=1计算百分位数",np.percentile(a,10,1))

输出结果：

数组a:
[[ 2 10 20]
[80 43 31]
[22 43 10]]

沿着axis=0计算百分位数： [ 6.  16.6 12. ]
沿着axis=1计算百分位数： [ 3.6 33.4 12.4]

numpy.median()

numpy.median() 用于计算 a 数组元素的中位数（中值）：

import numpy as np
a = np.array([[30,65,70],[80,95,10],[50,90,60]])
#数组a:
print(a)
#median()
print np.median(a)
#axis 0
print np.median(a, axis = 0)
#axis 1:
print(np.median(a, axis = 1))

输出结果如下：

数组a:
[[30 65 70]
[80 95 10]
[50 90 60]]
调用median()函数:
65.0
median(axis=0):
[ 50. 90. 60.]
median(axis=1):
[ 65. 80. 60.]

numpy.mean()

该函数表示沿指定的轴，计算数组中元素的算术平均值（即元素之总和除以元素数量）。示例如下：

import numpy as np
a = np.array([[1,2,3],[3,4,5],[4,5,6]]) 
print ('我们的数组是：')
print (a)
print ('调用 mean() 函数：')
print (np.mean(a))
print ('沿轴 0 调用 mean() 函数：')
print (np.mean(a, axis =  0))
print ('沿轴 1 调用 mean() 函数：')
print (np.mean(a, axis =  1))

输出结果：

我们的数组是：
[[1 2 3]
[3 4 5]
[4 5 6]]

调用 mean() 函数：
3.6666666666666665

沿轴 0 调用 mean() 函数：
[2.66666667 3.66666667 4.66666667]

沿轴 1 调用 mean() 函数：
[2. 4. 5.]

numpy.average()

加权平均值是将数组中各数值乘以相应的权数，然后再对权重值求总和，最后以权重的总和除以总的单位数（即因子个数）。

numpy.average() 根据在数组中给出的权重，计算数组元素的加权平均值。该函数可以接受一个轴参数 axis，如果未指定，则数组被展开为一维数组。

下面举一个简单的示例：现有数组 [1,2,3,4] 和相应的权重数组 [4,3,2,1]，它的加权平均值计算如下：

加权平均值=（1 * 4 + 2 * 3 + 3 * 2 + 4 * 1）/（4 + 3 + 2 + 1）

使用 average() 计算加权平均值，代码如下：

import numpy as np
a = np.array([1,2,3,4]) 
print('a数组是：')
print(a)
#average()函数：
print (np.average(a))
# 若不指定权重相当于对数组求均值
we = np.array([4,3,2,1]) 
#调用 average() 函数：')
print(np.average(a,weights = we))
#returned 为Ture，则返回权重的和 
prin(np.average([1,2,3,4],weights =  [4,3,2,1], returned =  True))

输出结果：

a数组是：
[1 2 3 4]

无权重值时average()函数：
2.5

有权重值时average()函数：
2.0

元组(加权平均值,权重的和)：
(2.0, 10.0)

在多维数组中，您也可以指定 axis 轴参数。示例如下：

import numpy as np
a = np.arange(6).reshape(3,2) 
#多维数组a
print (a)
#修改后数组
wt = np.array([3,5]) 
print (np.average(a, axis = 1, weights = wt))
#修改后数组
print (np.average(a, axis = 1, weights = wt, returned =  True))

输出结果为：

多维数组a：
[[0 1]
[2 3]
[4 5]]

axis=1按水平方向计算：
[0.625 2.625 4.625]

修改后的数组：
(array([0.625, 2.625, 4.625]), array([8., 8., 8.]))

方差np.var()

方差，在统计学中也称样本方差，如何求得方差呢？首先我们要知道全体样本的的平均值，然后再求得每个样本值与均值之差的平方和，最后对差的平方和求均值，公式如下（其中 n 代表元素个数）：

图1：方差公式

示例如下：

import numpy as np
print (np.var([1,2,3,4]))

输出结果：

1.25

标准差np.std()

标准差是方差的算术平方根，用来描述一组数据平均值的分散程度。若一组数据的标准差较大，说明大部分的数值和其平均值之间差异较大；若标准差较小，则代表这组数值比较接近平均值。它的公式如下：

std = sqrt(mean((x - x.mean())**2

NumPy 中使用 np.std() 计算标准差。示例如下：

import numpy as np
print (np.std([1,2,3,4]))

输出结果：

1.1180339887498949

NumPy排序和搜索功能

NumPy 提供了多种排序函数， 这些排序函数可以实现不同的排序算法。

排序算法特征主要体现在以下四个方面：执行速度，最坏情况下的复杂度，所需的工作空间以及算法的稳定性。下表列举了三种排序算法：

种类	速度	最坏复杂度	工作空间	稳定性
quicksort（快速排序）	1	O(n^2)	0	不稳定
mergesort（归并排序）	2	O(n * log(n)）	~n/2	稳定
heapsort（堆排序）	3	O(n * log(n))	0	不稳定

numpy.sort()

numpy.sort() 对输入数组执行排序，并返回一个数组副本。它具有以下参数：

numpy.sort(a, axis, kind, order)

参数说明：

• a：要排序的数组；
• axis：沿着指定轴进行排序，如果没有指定 axis，默认在最后一个轴上排序，若 axis=0 表示按列排序，axis=1 表示按行排序；
• kind：默认为 quicksort（快速排序）；
• order：若数组设置了字段，则 order 表示要排序的字段。

下面看一组示例：

import numpy as np 
a = np.array([[3,7],[9,1]]) 
print('a数组是：')
print(a)
#调用sort()函数
print(np.sort(a))
#按列排序：
print(np.sort(a, axis = 0))
#设置在sort函数中排序字段
dt = np.dtype([('name',  'S10'),('age',  int)])
a = np.array([("raju",21),("anil",25),("ravi",  17),  ("amar",27)], dtype = dt) 
#再次打印a数组
print(a)
#按name字段排序
print(np.sort(a, order = 'name'))

输出结果：

我们的数组是：
[[3 7]
[9 1]]

调用sort()函数：
[[3 7]
[1 9]]

按列排序：
[[3 1]
[9 7]]

再次打印a数组：
[(b'raju', 21) (b'anil', 25) (b'ravi', 17) (b'amar', 27)]
按name字段排序：
[(b'amar', 27) (b'anil', 25) (b'raju', 21) (b'ravi', 17)]

numpy.argsort()

argsort() 沿着指定的轴，对输入数组的元素值进行排序，并返回排序后的元素索引数组。示例如下：

import numpy as np 
a = np.array([90, 29, 89, 12]) 
print("原数组",a) 
sort_ind = np.argsort(a) 
print("打印排序元素索引值",sort_ind) 
#使用索引数组对原数组排序
sort_a = a[sort_ind] 
print("打印排序数组") 
for i in sort_ind: 
    print(a[i],end = " ")  

输出结果：

原数组:
[90 29 89 12]
打印排序元素的索引数组：
[3 1 2 0]
打印排序数组：
12 29 89 90 

numpy.lexsort()

numpy.lexsort() 按键序列对数组进行排序，它返回一个已排序的索引数组，类似于 numpy.argsort()。

下面看一组示例：

import numpy as np 
a = np.array(['a','b','c','d','e']) 
b = np.array([12, 90, 380, 12, 211]) 
ind = np.lexsort((a,b)) 
#打印排序元素的索引数组
print(ind) 
#使用索引数组对数组进行排序
for i in ind: 
    print(a[i],b[i])  

输出结果：

打印排序元素的索引数组：
[0 3 1 4 2]
使用索引数组对原数组进行排序：
a 12
d 12
b 90
e 211
c 380

NumPy 提供了许多可以在数组内执行搜索功能的函数。比如查找最值或者满足一定条件的元素。

numpy.nonzero()

该函数从数组中查找非零元素的索引位置。示例如下：

import numpy as np 
b = np.array([12, 90, 380, 12, 211]) 
print("原数组b",b) 
print("打印非0元素的索引位置") 
print(b.nonzero())  

输出结果：

原数组b
 [ 12  90 380  12 211]
打印非0元素的索引位置
(array([0, 1, 2, 3, 4]),)

numpy.where()

numpy.where() 的返回值是满足了给定条件的元素索引值。

import numpy as np 
b = np.array([12, 90, 380, 12, 211]) 
print(np.where(b>12)) 
c = np.array([[20, 24],[21, 23]]) 
print(np.where(c>20))  

输出结果：

返回满足条件的索引数组
(array([1, 2, 4]),)
(array([0, 1, 1]), array([1, 0, 1]))

numpy.extract()

该函数的返回值是满足了给定条件的元素值，示例如下：

import numpy as np
x = np.arange(9.).reshape(3, 3)
打印数组x:'
print(x) 
#设置条件选择偶数元素
condition = np.mod(x,2)== 0
#输出布尔值数组
print(condition)
#按condition提取满足条件的元素值
print np.extract(condition, x)

输出结果：

a数组是：[[0. 1. 2.][3. 4. 5.][6. 7. 8.]]输出布尔值数组：[[ True False  True][False  True False][ True False  True]]按条件提取元素：[0. 2. 4. 6. 8.]

numpy.argmax()

该函数返回最大值的的索引，与其相反的函数是 argmin() 求最小值索引 ，示例如下：

import numpy as np
a = np.array([[30,40,70],[80,20,10],[50,90,60]]) 
#a数组
print (a)
#argmax() 函数
print (np.argmax(a))
#将数组以一维展开
print (a.flatten())
#沿轴 0 的最大值索引：
maxindex = np.argmax(a, axis =  0) 
print (maxindex)
#沿轴 1 的最大值索引
maxindex = np.argmax(a, axis =  1) 
print (maxindex) 

输出结果：

数组a:
[[30 40 70]
[80 20 10]
[50 90 60]]

调用 argmax() 函数：
7

展开数组：
[30 40 70 80 20 10 50 90 60]

沿轴 0 的最大值索引：
[1 2 0]

沿轴 1 的最大值索引：
[2 0 1]

numpy.argmin()

argmin() 求最小值索引。示例如下：

import numpy as np
b= np.array([[3,4,7],[8,2,1],[5,9,6]]) 
print  ('数组b：')
print (b) 
#调用 argmin()函数
minindex = np.argmin(b) 
print (minindex)
#展开数组中的最小值：
print (b.flatten()[minindex])
#沿轴 0 的最小值索引：
minindex = np.argmin(b, axis =  0) 
print (minindex)
#沿轴 1 的最小值索引：
minindex = np.argmin(b, axis =  1) 
print (minindex)

输出结果：

数组b：
[[3 4 7]
[8 2 1]
[5 9 6]]
返回最小索引值：
5
#展开数组中的最小值：
1
#沿轴 0 的最小值索引：
[0 1 1]
#沿轴 1 的最小值索引：
[0 2 0]

NumPy字节交换

数据以字节的形式存储在计算机内存中，而存储规则可分为两类，即小端字节序与大端字节序。

小端字节序（little-endian），表示低位字节排放在内存的低地址端，高位字节排放在高地址段，它与大端字节序（big-endian）恰好相反。

对于二进制数 0x12345678，假设从地址 0x4000 开始存放，在大端和小端模式下，它们的字节排列顺序，如下所示：

图1：字节存储模式

小端存储后：0x78563412 大端存储后：0x12345678。

numpy.ndarray.byteswap()

该函数将数组中每个元素的字节顺序进行大小端调换。示例如下：

import numpy as np
a = np.array([1, 256, 8755], dtype = np.int16)
#数组a
print(a) 
#以16进制形式表示内存中的数据
print(map(hex,a)) 
#byteswap()函数通过传递True参数在适当的位置进行转换
#调用byteswap()函数
print(a.byteswap(True))
#十六进制形式
print(map(hex,a))

输出结果：

数组a
[ 1  256 8755]
以十六进制形式表示内存中的数据

NumPy Matrix矩阵库

NumPy 提供了一个 矩阵库模块numpy.matlib，该模块中的函数返回的是一个 matrix 对象，而非 ndarray 对象。矩阵由 m 行 n 列（m*n）元素排列而成，矩阵中的元素可以是数字、符号或数学公式等。

matlib.empty()

matlib.empty() 返回一个空矩阵，所以它的创建速度非常快。

numpy.matlib.empty(shape, dtype, order)

该函数的参数说明如下：

• shape：以元组的形式指定矩阵的形状。
• dtype：表示矩阵的数据类型。
• order：有两种选择，C（行序优先） 或者 F（列序优先）。

示例如下：

import numpy.matlib
import numpy as np
#矩阵中会填充无意义的随机值
print(np.matlib.empty((2,2)))

输出结果：

[[1.81191899e+167 6.65173396e-114]
[9.71613265e-243 6.96320200e-077]]

numpy.matlib.zeros()

numpy.matlib.zeros() 创建一个以 0 填充的矩阵，示例如下：

import numpy.matlib
import numpy as np
print(np.matlib.zeros((2,2))) 

输出结果：

[[ 0.  0.]
[ 0.  0.]] 

numpy.matlib.ones()

numpy.matlib.ones() 创建一个以 1 填充的矩阵。

import numpy.matlib
import numpy as np
print(np.matlib.ones((2,2)))

输出结果：

[[ 1.  1.]
[ 1.  1.]] 

numpy.matlib.eye()

numpy.matlib.eye() 返回一个对角线元素为 1，而其他元素为 0 的矩阵 。

numpy.matlib.eye(n,M,k, dtype)

• n：返回矩阵的行数；
• M：返回矩阵的列数，默认为 n；
• k：对角线的索引；
• dtype：矩阵中元素数据类型。

示例如下：

import numpy.matlib
import numpy as np
print (np.matlib.eye(n =  3, M =  4, k =  0, dtype =  float))

输出结果：

[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]]

numpy.matlib.identity()

该函数返回一个给定大小的单位矩阵，矩阵的对角线元素为 1，而其他元素均为 0。

import numpy.matlib
import numpy as np
print np.matlib.identity(5, dtype = float)

输出结果：

[[ 1.  0.  0.  0.  0.]
[ 0.  1.  0.  0.  0.]
[ 0.  0.  1.  0.  0.]
[ 0.  0.  0.  1.  0.]
[ 0.  0.  0.  0.  1.]]

numpy.matlib.rand()

numpy.matlib.rand() 创建一个以随机数填充，并给定维度的矩阵。示例如下：

import numpy.matlib
import numpy as np
print (np.matlib.rand(3,3))

示例如下：

[[0.23966718 0.16147628 0.14162   ]
[0.28379085 0.59934741 0.62985825]
[0.99527238 0.11137883 0.41105367]]

这里需要注意，因为 matrix 只能表示二维数据，而 ndarray 也可以是二维数组，所以两者可以互相转换。示例如下：

#创建矩阵i
import numpy.matlib
import numpy as np 
i = np.matrix('1,2;3,4') 
print (i)

输出结果：

[[1  2]
[3  4]]

实现 matrix 与 ndarray 之间的转换，如下所示：

import numpy.matlib
import numpy as np 
j = np.asarray(i) 
print (j)
k = np.asmatrix (j)
print (k)

输出结果：

ndarray：
[[1  2]
[3  4]]
matrix：
[[1  2]
[3  4]] 

NumPy线性代数

NumPy 提供了 numpy.linalg 模块，该模块中包含了一些常用的线性代数计算方法，下面对常用函数做简单介绍：

函数名称	描述说明
dot	两个数组的点积。
vdot	两个向量的点积。
inner	两个数组的内积。
matmul	两个数组的矩阵积。
det	计算输入矩阵的行列式。
solve	求解线性矩阵方程。
inv	计算矩阵的逆矩阵，逆矩阵与原始矩阵相乘，会得到单位矩阵。

numpy.dot()

按照矩阵的乘法规则，计算两个矩阵的点积运算结果。当输入一维数组时返回一个结果值，若输入的多维数组则同样返回一个多维数组结果。

输入一维数组，示例如下：

import numpy as np
A=[1,2,3]
B=[4,5,6]
print(np.dot(A,B))

输出结果：

32

输入二维数组时，示例如下：

import numpy as np 
a = np.array([[100,200],
             [23,12]]) 
b = np.array([[10,20],
            [12,21]]) 
dot = np.dot(a,b) 
print(dot) 

输出结果：

[[3400 6200]
[ 374  712]]

对于上述输出结果，它的计算过程如下：

[[10010+20012,10020+20021]

[2310+1212,2320+1221]]

点积运算就是将 a 数组的每一行元素与 b 数组的每一列元素相乘再相加。

numpy.vdot()

该函数用于计算两个向量的点积结果，与 dot() 函数不同。

import numpy as np 
a = np.array([[100,200],[23,12]]) 
b = np.array([[10,20],[12,21]]) 
vdot = np.vdot(a,b) 
print(vdot)  

输出结果：

5528

numpy.inner()

inner() 方法用于计算数组之间的内积。当计算的数组是一维数组时，它与 dot() 函数相同，若输入的是多维数组则两者存在不同，下面看一下具体的实例。

import numpy as np
A=[[1 ,10],
    [100,1000]]
B=[[1,2],
    [3,4]]
#inner函数
print(np.inner(A,B))
#dot函数
print(np.dot(A,B))

输出结果：

[[ 21 43]
[2100 4300]]

[[ 31 42]
[3100 4200]]

inner() 函数的计算过程是 A 数组的每一行与 B 数组的每一行相乘再相加，如下所示：

[[1*1+2*10  1*3+10*4 ]
[100*1+1000*2  100*3+1000*4]]

dot() 则表示是 A 数组每一行与 B 数组的每一列相乘。

numpy.matmul()

该函数返回两个矩阵的乘积，假如两个矩阵的维度不一致，就会产生错误。

import numpy as np 
a = np.array([[1,2,3],[4,5,6],[7,8,9]]) 
b = np.array([[23,23,12],[2,1,2],[7,8,9]]) 
mul = np.matmul(a,b) 
print(mul)  

输出结果：

[[ 48  49  43]
[144 145 112]
[240 241 181]]

numpy.linalg.det()

该函数使用对角线元素来计算矩阵的行列式，计算 2*2（两行两列） 的行列式，示例如下：

[[1,2],
 [3,4]]

通过对角线元素求行列式的结果（口诀：“一撇一捺”计算法）：

14-23=-2

我们可以使用 numpy.linalg.det() 函数来完成计算。示例如下：

import numpy as np 
a = np.array([[1,2],[3,4]]) 
print(np.linalg.det(a))  

输出结果：

-2.0000000000000004

numpy.linalg.solve()

该函数用于求解线性矩阵方程组，并以矩阵的形式表示线性方程的解，如下所示：

3X  +  2 Y + Z =  10  
X + Y + Z = 6
X + 2Y - Z = 2

首先将上述方程式转换为矩阵的表达形式：

方程系数矩阵：
3   2   1 
1   1   1 
1   2  -1
方程变量矩阵:
X 
Y 
Z  
方程结果矩阵：
10 
6
2

如果用 m 、x、n 分别代表上述三个矩阵，其表示结果如下：

m*x=n 或 x=n/m

将系数矩阵与结果矩阵传递给 numpy.solve() 函数，即可求出线程方程的解，如下所示：

import numpy as np
m = np.array([[3,2,1],[1,1,1],[1,2,-1]])
print ('数组 m：')
print (m)
print ('矩阵 n：')
n = np.array([[10],[6],[2]])
print (n)
print ('计算：m^(-1)n：')
x = np.linalg.solve(m,n)
print (x)

输出结果：

x为线性方程的解：
[[1.]
[2.]
[3.]]

numpy.linalg.inv()

该函数用于计算矩阵的逆矩阵，逆矩阵与原矩阵相乘得到单位矩阵。示例如下：

import numpy as np 
a = np.array([[1,2],[3,4]]) 
print("原数组:",a) 
b = np.linalg.inv(a) 
print("求逆:",b)  

输出结果：

原数组:
[[1 2]
[3 4]]
求逆:
[[-2.   1. ]
[ 1.5 -0.5]]

NumPy矩阵乘法

矩阵乘法是将两个矩阵作为输入值，并将 A 矩阵的行与 B 矩阵的列对应位置相乘再相加，从而生成一个新矩阵，如下图所示：

注意：必须确保第一个矩阵中的行数等于第二个矩阵中的列数，否则不能进行矩阵乘法运算。

图1：矩阵乘法

矩阵乘法运算被称为向量化操作，向量化的主要目的是减少使用的 for 循环次数或者根本不使用。这样做的目的是为了加速程序的计算。

下面介绍 NumPy 提供的三种矩阵乘法，从而进一步加深对矩阵乘法的理解。

逐元素矩阵乘法

multiple() 函数用于两个矩阵的逐元素乘法，示例如下：

import numpy as np 
array1=np.array([[1,2,3],[4,5,6],[7,8,9]],ndmin=3) 
array2=np.array([[9,8,7],[6,5,4],[3,2,1]],ndmin=3) 
result=np.multiply(array1,array2) 
result  

输出结果：

array([[[ 9, 16, 21],
         [24, 25, 24],
         [21, 16,  9]]])

矩阵乘积运算

matmul() 用于计算两个数组的矩阵乘积。示例如下：

import numpy as np 
array1=np.array([[1,2,3],[4,5,6],[7,8,9]],ndmin=3) 
array2=np.array([[9,8,7],[6,5,4],[3,2,1]],ndmin=3) 
result=np.matmul(array1,array2) 
print(result) 

输出结果：

数组（[[[
         [30，24，18]，
         [84，69，54 ]，[138，114，90]]]）

矩阵点积

dot() 函数用于计算两个矩阵的点积。如下所示：

示例如下：

import numpy as np 
array1=np.array([[1,2,3],[4,5,6],[7,8,9]],ndmin=3) 
array2=np.array([[9,8,7],[6,5,4],[3,2,1]],ndmin=3) 
result=np.dot(array1,array2) 
print(result)  

输出结果：

array([[[[ 30,  24,  18]],
         [[ 84,  69,  54]],
         [[138, 114,  90]]]])

NumPy和Matplotlib绘图

Matplotlib 是 Python 的绘图库，它经常与 NumPy 一起使用，从而提供一种能够代替 Matlab 的方案。不仅如此 Matplotlib 还可以与 PyQt 和 wxPython 等图形工具包一起使用。

Matplotlib 最初由 John D. Hunter 编写，目前，它的最新的版本是 3.3.1，最后一个支持 Python 2 的版本是 2.2.5 。您可以通过 Python 包管理器 pip 来安装 Matplotlib，命令如下：

pip3 install matplotlib

安装成功后，我们可以使用下面的引包方式，将其导入：

from matplotlib import pyplot as plt

绘制线性函数图像

Matplotlib 的子模块模块 pyplot 是用来绘制 2D 图像的重要模块。下面示例绘制了函数 y = 2x + 5 的图像：

import numpy as np
from matplotlib import pyplot as plt
x = np.arange(1,11)
y = 2 * x + 5
#绘制坐标标题
plt.title("Matplotlib demo")
#绘制x、y轴备注
plt.xlabel("x axis")
plt.ylabel("y axis")
plt.plot(x,y)
plt.show()

输出结果如下：

图1：Matplotlib绘制线性图

您可以向 plot() 函数中添加格式化字符，来实现不同样式的显示或标记。 下表列举了常用的格式化字符：

字符	描述
‘-’	实线样式
‘–’	短横线样式
‘-.’	点划线样式
‘:’	虚线样式
‘.’	点标记
‘,’	像素标记
‘o’	圆标记
‘v’	倒三角标记
‘^’	正三角标记
‘<’	左三角标记
‘>’	右三角标记
‘1’	下箭头标记
‘2’	上箭头标记
‘3’	左箭头标记
‘4’	右箭头标记
‘s’	正方形标记
‘p’	五边形标记
‘*’	星形标记
‘h’	六边形标记 1
‘H’	六边形标记 2
‘+’	加号标记
‘x’	X 标记
‘D’	菱形标记
‘d’	窄菱形标记
‘|’	竖直线标记
‘_’	水平线标记

同时 Matplotlib 还定义了一些颜色字符，如下所示：

字符	颜色
‘b’	蓝色
‘g’	绿色
‘r’	红色
‘c’	青色
‘m’	品红色
‘y’	黄色
‘k’	黑色
‘w’	白色

如果想要以圆点的样式，来代替图 1 中的线条样式，那么可以使用“ ob”作为 plot() 的格式化字符。如下所示：

import numpy as np
from matplotlib import pyplot as plt
x = np.arange(1,11)
y = 2 * x + 5
plt.title("Matplotlib demo1")
plt.xlabel("x axis")
plt.ylabel("y axis")
plt.plot(x,y,"ob")
plt.show() 

输出结果如下图：

图2：Matplotlib绘制圆点图

绘制正弦波图

您也可以使用 Matplotlib 生成正弦波图。示例如下：

import numpy as np
import matplotlib.pyplot as plt 
# 计算正弦曲线上的x和y坐标
x = np.arange(0, 3 * np.pi, 0.1)
y = np.sin(x)
plt.title("sine wave image")
# 使用matplotlib制图
plt.plot(x, y)
plt.show() 

输出结果：

图3：Matplotlib绘图正弦图

subplot()

subplot() 允许您在同一画布中的不同位置绘制多个图像，可以理解为对画布按行、列分割，函数的语法格式如下：

plt.subplot(nrows, ncols, index, **kwargs)

参数说明：该函数使用三个整数描述子图的位置信息，这三个整数是行数、列数和索引值（此处索引值从1开始），子图将分布在设定的索引位置上。从右上角增加到右下角。比如，plt.subplot(2, 3, 5) 表示子图位于 2 行 3 列 中的第 5 个位置上。

图4：subplot画布分割

下面示例是在同一画布中绘制正弦和余弦图像，代码如下：

import numpy as np
import matplotlib.pyplot as plt 
  
#计算正弦和余弦曲线上的点的 x 和 y 坐标 
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x) 
  
#绘制subplot 网格为2行1列
#激活第一个 subplot
plt.subplot(2, 1, 1)
#绘制第一个图像
plt.plot(x, y_sin)
plt.title('Sine') 
#将第二个 subplot 激活，并绘制第二个图像
plt.subplot(2, 1, 2)
plt.plot(x, y_cos)
plt.title('Cosine')
#展示图像
plt.show()

输出结果如下：

图5：Matplotlib绘制波形图

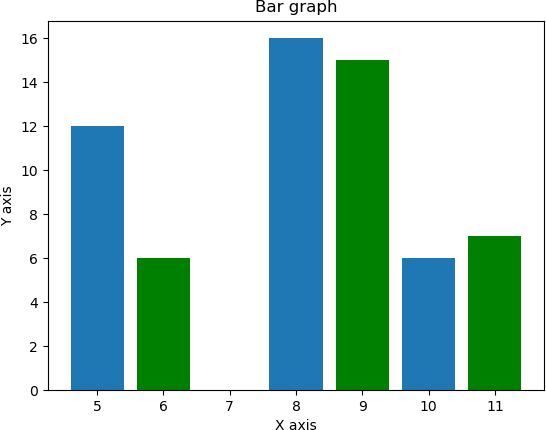
bar()柱状图

pyplot 子模块中提供了 bar() 函数来生成柱状图。下面示例代码，生成了两组数据的柱状图：

from matplotlib import pyplot as plt
#第一组数据
x1 = [5,8,10]
y1 = [12,16,6] 
#第二组数据
x2 = [6,9,11]
y2 = [6,15,7]
plt.bar(x1, y1, align = 'center')
plt.bar(x2, y2, color = 'g', align = 'center')
plt.title('Bar graph')
#设置x轴与y轴刻度
plt.ylabel('Y axis')
plt.xlabel('X axis') 
plt.show()

输出结果：

图6：Matplotlib绘制柱状图

numpy.histogram()

直方图是一种表示数据概率分布的常用图形。NumPy 提供了 histogram() 函数，它以直方图的形式表示一组数据的概率分布值。

histogram() 函数有两个返回值，分别是 hist 与 bin_edges，分别代表直方图高度值与 bin 数值区间范围， 函数的语法格式如下：

histogram(array,bins=10,range=None,weights=None,density=False)

示例如下：

import numpy as np 
a = np.arange(8) 
hist, bin_edges = np.histogram(a, density=True) 

输出结果如下：

his：
[0.17857143 0.17857143 0.17857143 0.         0.17857143 0.17857143
 0.         0.17857143 0.17857143 0.17857143]
bin_edges
[0.  0.7 1.4 2.1 2.8 3.5 4.2 4.9 5.6 6.3 7. ]

numpy.histogram() 将输入数组 a 和 bins 作为两个参数，其中 bins 数组的连续元素作为 bin 区间的边界值。示例如下：

import numpy as np
a = np.array([22,87,5,43,56,73,55,54,11,20,51,5,79,31,27])
np.histogram(a,bins = [0,20,40,60,80,100])
hist,bins = np.histogram(a,bins = [0,20,40,60,80,100]) 
print(hist)
print(bins)

输出结果如下：

返回hist直方图值：
[3 4 5 2 1]
返回bin区间边缘值：
[0 20 40 60 80 100]

plt()

pyplot 子模块的 plt() 函数将一个输入数组和 bins 数组作为参数，并将其输出为直方图。示例如下：

from matplotlib import pyplot as plt
import numpy as np 
a = np.array([22,87,5,43,56,73,55,54,11,20,51,5,79,31,27])
plt.hist(a, bins =  [0,20,40,60,80,100])
plt.title("histogram")
plt.show()

输出图像如下所示：

图7：Matplotlib直方图

NumPy IO操作

NumPy IO 操作是以文件的形式从磁盘中加载 ndarray 对象。在这个过程中，NumPy 可以两种文件类型处理 ndarray 对象，一类是二进制文件（以.npy结尾），另一类是普通文本文件。

上述两种文件格式，分别对应着不同的 IO 方法，如下所示：

文件类型	处理方法
二进制文件	load() 和 save()
普通文本文件	loadtxt() 和 savetxt()

我们知道，文件会被保存在不同的计算机上（比如 Linux、Windows、MacOSX 等）。为了不受的计算机架构影响，NumPy 开发团队给 ndarray 对象引入了一种.npy文件格式，通过它来件实现对 ndarray 对象的保存。

numpy.save()

numpy.save() 方法将输入数组存储在.npy文件中。

numpy.save(file, arr, allow_pickle=True, fix_imports=True)

参数说明：

• file：保存后的文件名称，其文件类型为.npy；
• arr：要保存的数组
• allow_pickle：可选项，布尔值参数，允许使用 pickle 序列化保存数组对象。
• fix_imports：可选项，为了便于在 Pyhton2 版本中读取 Python3 保存的数据。

示例如下：

import numpy as np
a = np.array([1,2,3,4,5])
np.save('first',a)

使用 load() 从 first.npy 文件中加载数据，如下所示：

import numpy as np
b = np.load('outfile.npy')
print( b) 

输出结果如下：

[1, 2, 3, 4, 5]

savetxt()

savetxt() 和 loadtxt() 分别表示以文本格式存储数据或加载数据。其中 savetxt() 的语法格式如下：

np.savetxt(‘filename文件路径’, self.task, fmt="%d", delimiter=" ")

参数说明：

• filename：表示保存文件的路径；
• self.task： 要保存数组的变量名；
• fmt="%d"： 指定保存文件的格式，默认是十进制；
• delimiter=" "表示分隔符，默认以空格的形式隔开。

示例如下：

import numpy as np
a = np.array([1,2,3,4,5])
np.savetxt('second.txt',a)
#使用loadtxt重载数据
b = np.loadtxt('second.txt')
print(b) 

输出结果：

[ 1. 2. 3. 4. 5.]