一元线性回归模型的原理及实现

一元线性回归

​由于笔者的数学不太好，而且网上关于一元线性回归的文章有很多，所以相关内容大家可以查找一下，这里我就简单的搬运一下简单概念。

一元线性回归的方程：
$$h(x)={\beta }_0+{\beta }_{1}x$$
其中第一个参数${\beta }_0$为截距，第二个参数${\beta }_1$为斜率。

代价函数

​ 回归分析的主要目的是通过已有的信息，去推测出未知的信息。通过一个例子大家可能会更深刻的理解回归分析的目的。

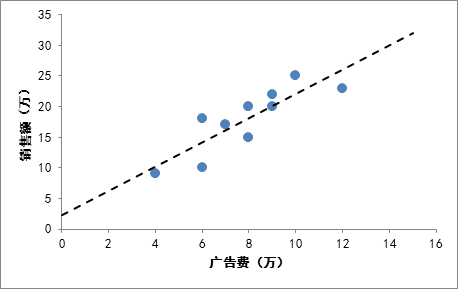
上图为广告费与销售额的关系图，虚线为我们的一元线性回归方程，通过回归分析，我们可以预测当广告费为14万元时，我们的销售额可能是30万元。

​回归分析属于统计学问题，这就说明在给定自变量x时，我们是无法准确的得出因变量y的。但是我们可以通过一些方法去**“减少误差”**，使得预测的结果尽量的接近真实值。所以我们引入了代价函数，其使用最小二乘法的理论去减少这种误差。代价函数数学公式如下：
$$J({\beta }_0,{\beta }_1)=\frac{1}{2m}\sum _{i=1}^m[y_i-h(x_i){]}^2$$
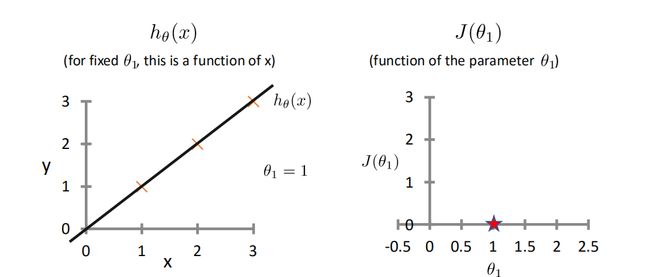
​ 为了更好的理解代价函数，这里使第一个参数为零，然后观察一下图片（由于是从视频中截取的图片，所以这里的参数又β变成了θ，是我太懒了）

当θ=1时，此时回归方程贯穿每一个点，所以误差为零，J(θ)值如右图所示。

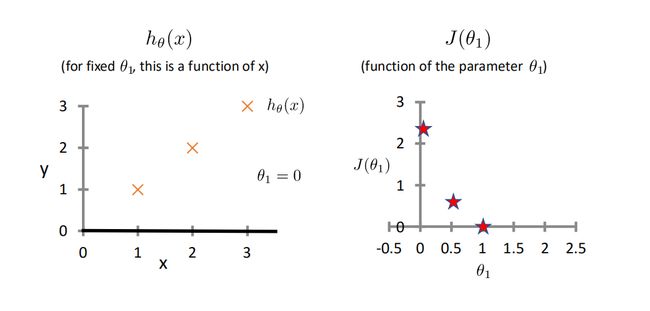
当θ=0.5时，我们一顿计算可得，J(θ)≈0.58

当θ=0时，我们同样可以计算出J(θ)的值。

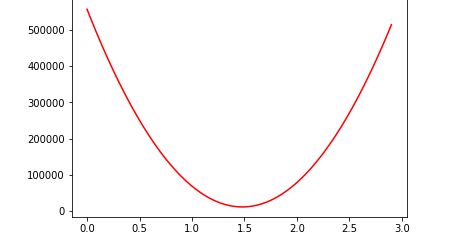
如果我们大量的将θ带入，我们将得到如下的代价函数图

由此我们可以清晰地看到，J(θ)在某一点处是可以取到最小值的，这就是我们的引入代价函数的目的：通过调整参数来减少误差，使得预测的结果尽量的接近真实值。

注：最小二乘法的公式如下：
$$\sum [y_i-({\beta }_0+{\beta }_1{x}_i){]}^2$$

梯度下降法

​梯度下降法就是一个很好的调整参数的方法，它可以通过下面公式不断调整${\beta }_0$和${\beta }_1$的值，从而得到一个全局最小值，或者是一个局部最小值。
$$\begin{gathered} repeatuntilconvergence\{ \\ {\beta }_j={\beta }_j-\alpha \frac{\partial }{\partial {\beta }_j}J({\beta }_0,{\beta }_1) \\ forj=1andj=0 \\ \} \end{gathered}$$
其中α称为学习率(learning rate)，而学习率就是步长，学习率大，一次跨越的距离就远，这样可能会错过全局（局部）最小值点；学习率小，一次跨越的距离就短，这样会花费比较多的时间来处理数据。

求偏导后：
$$\begin{gathered} j=0:{\beta }_0={\beta }_0-\alpha (\frac{1}{m}\sum _{i=1}^m(y_i-{\beta }_0-{\beta }_1{x}_i)\ast -1) \\ ={\beta }_0-\alpha (-\frac{1}{m}\sum _{i=1}^m[y_i-({\beta }_1{x}_i+{\beta }_0)]) \\ ={\beta }_0-\alpha (-\frac{1}{m}\sum _{i=1}^m[y_i-(h(x_i)]) \\ j=1:{\beta }_1={\beta }_1-\alpha (\frac{1}{m}\sum _{i=1}^m(y_i-{\beta }_0-{\beta }_1{x}_i)\ast -x_i) \\ ={\beta }_1-\alpha (-\frac{1}{m}\sum _{i=1}^m{x}_i[y_i-({\beta }_1{x}_i+{\beta }_0)]) \\ ={\beta }_1-\alpha (-\frac{1}{m}\sum _{i=1}^m{x}_i[y_i-(h(x_i)]) \end{gathered}$$

代码实现：

import numpy as np
import matplotlib.pyplot as plt
#载入数据
data = np.genfromtxt("data.csv",delimiter=",")#delimiter分隔符，此分隔符为，
x_data = data[:,0]
y_data = data[:,1]
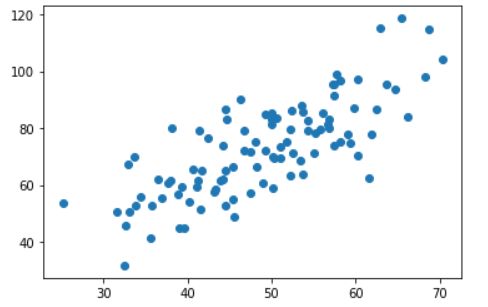
plt.scatter(x_data,y_data)
plt.show()

#学习率 learning rate
lr = 0.0001
#截距
b = 0
#斜率
k = 0
#最大迭代次数
epochs = 50

#最小二乘法
def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
    return totalError / float(len(x_data)) /2.0 #最小二乘法法公式

def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    #计算总数据量
    m = float(len(x_data))
    #循环epochs次
    for i in range(epochs):
        b_grad = 0
        k_grad = 0
        #计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            b_grad += -(1/m)*(y_data[j]-(k * x_data[j] + b))
            k_grad += -(1/m)*x_data[j] * (y_data[j] - (k * x_data[j] + b))
        #更新b和k
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)
         # 每迭代5次，输出一次图像
''' 方面查看变化趋势
			if i % 5==0:
            print("epochs:",i)
            plt.plot(x_data, y_data, 'b.')
            plt.plot(x_data, k*x_data + b, 'r')
            plt.show()
            '''
    return b, k

b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
#画图
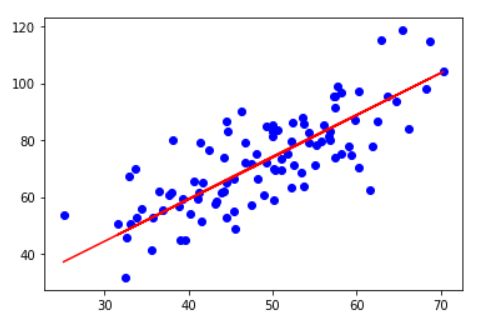
plt.scatter(x_data, y_data, c='b')
plt.plot(x_data, k*x_data + b, 'r')
plt.show()