多智能体系统的分布式协同控制——采样控制、脉冲控制、弹性控制
导读
多智能体系统协同控制领域的研究重点:一致性问题、编队控制、群集效应、蜂拥理论、空间聚集、分布式滤波与优化。集体行为的基本规则是什么呢?人们可以仅使用局部信息设计适当的控制协议来实现某些特定的集体运动吗?一致性问题,其核心目标是如何设计合适的控制协议或者机制使得网络中的所有节点的状态能够达到一致。
把实际问题转化为科学研究的范畴,离不开系统建模。把多智能系统抽象为点和边构成的网络系统,每个节点就代表实际中的每个智能体,智能体通过相互连接所构成的网络系统,体现智能体间的连接作用。
目录
一、无leader网络与leader-follower网络
1.1 无leader网络
1.2 leader-follower网络
1.3 分布式协同控制三要素
二、分布式采样控制[1]
2.1 随机采样模型
2.2 随机采样模型转化
2.3 一致性结论
三、分布式脉冲控制[2-3]
3.1、 分布式脉冲控制模型建立
3.2、 问题描述
3.3 脉冲牵制可控性
3.4 网络化分布式脉冲控制
四、弹性控制
一、无leader网络与leader-follower网络
1.1 无leader网络
无leader网络的含义是智能体通过彼此之间的信息交互实现协同,如图1所示。 是加权邻接矩阵,如果智能体可以收到智能体的信息,那么,否则 。 是耦合强度,表示智能体之间的连接紧密程度,与的值成正比。拉普拉斯矩阵被定义为,。一致性在数学上表示为,,当时间趋于无穷大时,状态趋于0。
图1 无领导者网络
1.2 leader-follower网络
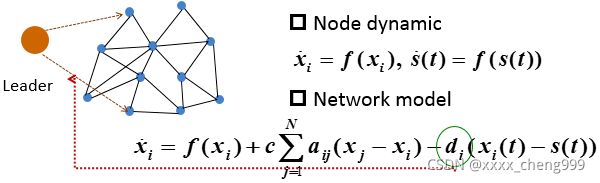
在 leader-follower网络中存在领导者智能体,系统的调控目标是使得跟随者智能体和领导者智能体实现一致,如图2所示。与无领导者网络相比多了 参数,表示领导者的信息反馈在系统动态上。当且仅当存在从领导者到第i个节点的有向路径时。节点称为牵制节点或受控节点。其目的是通过控制少量的追随者,即牵制控制,来驱动追随者与领导者同步,公式化为:
图2 领导者跟随网络
1.3 分布式协同控制三要素
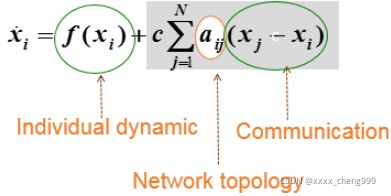
影响智能体群体行为的因素主要包含:智能体自身动态,网络拓扑(即智能体之间连接),通讯机制三个方面,如图3所示。阴影部分就称之为分布式控制协议。我们的目标是设计高效的分布式协同控制协议,尽可能多的减少智能体之间的通信,且保持系统性能。
图3 分布式协同控制三要素
高效的分布式控制协可分为时间触发机制和事件触发机制两种。
时间触发机制包括 分布式采样控制和 分布式脉冲控制;
事件触发机制包括 分布式事件触发控制;此外还有恶意攻击下的 弹性控制。
二、分布式采样控制[1]
2.1 随机采样模型
图4 随机采样模型
2.2 随机采样模型转化
图5 随机采样模型处理
2.3 一致性结论
问题1:随着智能体数量N的增加,大规模网络如何求解?解决方式如图6所示,将leader-follower一致性问题转化为一个leader和两个-follower的问题。
图6 随机采样一致性结论
问题2:如何设计网络实现leader-follower一致?解决方式如图7所示,将leader-follower一致性问题转化为一个leader和一个follower的同步问题,寻找m的上下界设计网络。
图7 随机采样一致性网络设计
三、分布式脉冲控制[2-3]
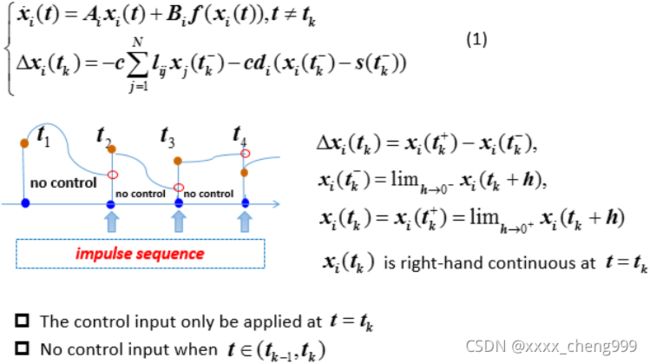
3.1、 分布式脉冲控制模型建立
文献[2]的目标是使得异质网络与领导者通过分布式脉冲控制实现拟同步(有界同步)。
图8 分布式脉冲控制模型
图9 脉冲控制
3.2、 问题描述
图10 异质网络分布式脉冲控制
(1)如何精确的估计拟同步误差上界?
(2)如何设计耦合强度,选择牵制节点,确定脉冲间隔, 优化误差上界?
(3)应该牵制多少个节点以及选择哪些节点?
在脉冲间隔没有限制的情况下,如果网络连通,则仅牵制一个节点是有效的;如果网络不连通,牵制节点的最小数目是网络的连通分支数目,与连续反馈牵制控制的结论吻合;耦合强度有上界,不能太大,较小的更合适。
(4)在给定的误差水平下,如何设计耦合强度,选择牵制节点,确定脉冲间隔?
3.3 脉冲牵制可控性
给定一个网络,根据实现准同步所需的耦合强度c,控制矩阵D和脉冲间隔d的值来定义脉冲牵制可控性。用两个关键指标来定义和评估脉冲可控制性。和越低,网络的脉冲牵制就越容易控制。
图11 脉冲可控性
3.4 网络化分布式脉冲控制
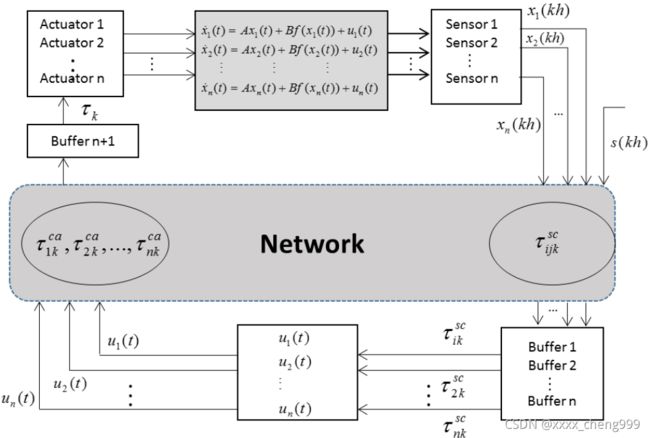
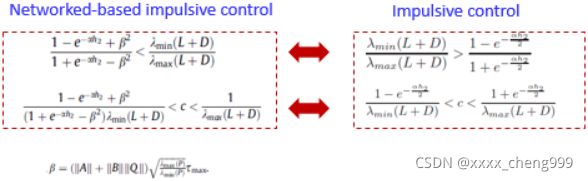
若采用远程控制方案如图12所示,则分布式控制协议的设计需要考虑网络延时的影响,系统模型如图13所示,通过对比发现,网络延时对一致性的实现起着负作用,将会增大牵制矩阵的控制比率,意味着需要牵制更多的节点,如图14所示。
图12 网络化控制
图13 网络化分布式控制的数学模型
图14 分布式脉冲控制与网络化分布式脉冲控制结果对比
四、弹性控制
弹性控制(Resiliently Control)是指对网络攻击具有一定的容忍度且能够自我恢复的控制策略,控制策略能够适应组织内部条件与外部环境的变化,具有灵活性。
基于时间或者事件触发的控制方法大多考虑的是确定性时间序列,实际中攻击序列具有很大的随机性,如何处理随机攻击时间序列的场景?
下面提供了一种具有随机脉冲攻击序列的系统稳定性的分析方法。
图15 随机脉冲攻击序列系统模型
参考文献:
[1] Wangli He, Biao Zhang, Qing-Long Han. Feng Qian, Jürgen Kurths, Jinde Cao. Leader-following consensus of nonlinear multi-agent systems with stochastic sampling. IEEE Transactions on Cybernetics, 2017, 47(2): 327-338
[2] Wangli He, Feng Qian, James Lam, Guanrong Chen, Qing-Long Han and Jürgen Kurths, Quasi-synchronization of heterogeneous dynamic networks via distributed impulsive control: error estimation, optimization and design. Automatica, 2015, 62: 249-262
[3] Wangli He, Guanrong Chen, Qing-Long Han and Feng Qian, Network-based Leader-following consensus of nonlinear multi-agent systems via distributed impulsive control. Information Sciences, 2017, 380: 145-158