计算几何向量叉乘

Calculate the number of toys that land in each bin of a partitioned toy box.
Mom and dad have a problem - their child John never puts his toys away when he is finished playing with them. They gave John a rectangular box to put his toys in, but John is rebellious and obeys his parents by simply throwing his toys into the box. All the toys get mixed up, and it is impossible for John to find his favorite toys.

John’s parents came up with the following idea. They put cardboard partitions into the box. Even if John keeps throwing his toys into the box, at least toys that get thrown into different bins stay separated. The following diagram shows a top view of an example toy box.

For this problem, you are asked to determine how many toys fall into each partition as John throws them into the toy box.
Input
The input file contains one or more problems. The first line of a problem consists of six integers, n m x1 y1 x2 y2. The number of cardboard partitions is n (0 < n <= 5000) and the number of toys is m (0 < m <= 5000). The coordinates of the upper-left corner and the lower-right corner of the box are (x1,y1) and (x2,y2), respectively. The following n lines contain two integers per line, Ui Li, indicating that the ends of the i-th cardboard partition is at the coordinates (Ui,y1) and (Li,y2). You may assume that the cardboard partitions do not intersect each other and that they are specified in sorted order from left to right. The next m lines contain two integers per line, Xj Yj specifying where the j-th toy has landed in the box. The order of the toy locations is random. You may assume that no toy will land exactly on a cardboard partition or outside the boundary of the box. The input is terminated by a line consisting of a single 0.
Output
The output for each problem will be one line for each separate bin in the toy box. For each bin, print its bin number, followed by a colon and one space, followed by the number of toys thrown into that bin. Bins are numbered from 0 (the leftmost bin) to n (the rightmost bin). Separate the output of different problems by a single blank line.
Sample Input
5 6 0 10 60 0
3 1
4 3
6 8
10 10
15 30
1 5
2 1
2 8
5 5
40 10
7 9
4 10 0 10 100 0
20 20
40 40
60 60
80 80
5 10
15 10
25 10
35 10
45 10
55 10
65 10
75 10
85 10
95 10
0
Sample Output
0: 2
1: 1
2: 1
3: 1
4: 0
5: 1

0: 2
1: 2
2: 2
3: 2
4: 2
Hint
As the example illustrates, toys that fall on the boundary of the box are “in” the box.

翻译

计算一个分区玩具箱中每个箱子里的玩具数量。
妈妈和爸爸有个问题-他们的孩子约翰玩完玩具后从不把它们放好。他们给了约翰一个长方形的盒子，让他把玩具放进去，但约翰很叛逆，只需把玩具扔进盒子里，就服从了父母。所有的玩具都混在一起了，约翰不可能找到他最喜欢的玩具。
约翰的父母想出了以下主意。他们把纸板隔板放进箱子里。即使约翰一直把玩具扔进箱子里，至少扔进不同箱子的玩具是分开的。下图显示了一个示例玩具盒的顶视图。
对于这个问题，当John把玩具扔进玩具盒时，你需要确定每个分区中有多少玩具。
输入
输入文件包含一个或多个问题。问题的第一行由六个整数组成，n m x1 y1 x2 y2。纸板隔板的数量为n（0 输出
每个问题的输出将是玩具盒中每个单独箱子的一行。对于每个箱子，打印箱子编号，后跟冒号和一个空格，后跟扔进箱子的玩具数量。箱子编号从0（最左边的箱子）到n（最右边的箱子）。用一个空行分隔不同问题的输出。
样本输入
5 6 0 10 60 0
3 1
4 3
6 8
10 10
15 30
1 5
2 1
2 8
5 5
40 10
7 9
4 10 0 10 100 0
20 20
40 40
60 60
80 80
5 10
15 10
25 10
35 10
45 10
55 10
65 10
75 10
85 10
95 10
0
样本输出
0: 2
1: 1
2: 1
3: 1
4: 0
5: 1
0: 2
1: 2
2: 2
3: 2
4: 2
提示
如示例所示，落在盒子边界上的玩具“在”盒子中。

思路

**有一个玩具盒，被n个隔板分开成左到u右n+1个区域，然后给每个玩具的坐标，求每个区域有几个玩具。
题解：依次用叉积判断玩具在每个隔板左边还是右边。利用向量叉乘判断点在线的哪一边，当叉乘小于等于0时，点在线的左边，否则在右边

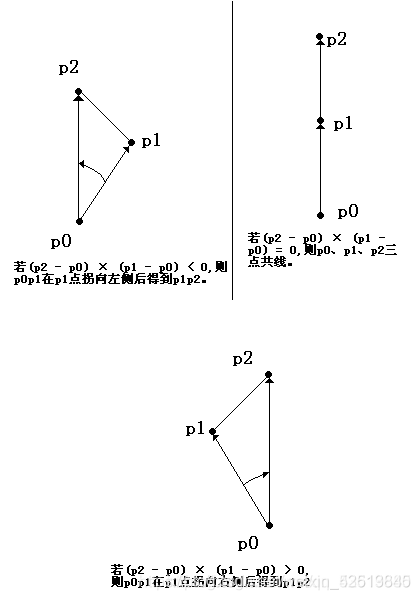
（p2-p0）X(p1-p0)>0则p1在线的右边

（p2-p0）X(p1-p0)<0则p1在线的左边

#include
#include
int q(int x1,int y1,int x2,int y2)
{
	return (x1*y2)-(x2*y1);
}
int main()
{
	int n,u[52000],l[52000],m,x1,x2,y1,y2,i,j,x,y;
	int s[52000];
	while(~scanf("%d",&n)&&n)
	{
		memset(s,0,sizeof(s));
		scanf("%d%d%d%d%d",&m,&x1,&y1,&x2,&y2);
		for(i=0;i<n;i++)
			scanf("%d%d",&u[i],&l[i]);
		for(i=0;i<m;i++)
		{
			scanf("%d%d",&x,&y);
			for(j=0;j<n;j++)
			if(q(x-l[j],y-y2,u[j]-l[j],y1-y2)<=0)
			break;
			s[j]++;
		}
		for(i=0;i<=n;i++)
			printf("%d: %d\n",i,s[i]);
			printf("\n");
	}
}