趣味编程：三门问题

三门问题，也称为蒙提霍尔问题（Monty Hall Problem）。

你在参加一个节目，面前是三扇关闭着的门。其中一扇后面是小汽车，选中它就可赢得汽车，另外两扇后面各是一只羊。你选择了其中一扇，但没有打开它，这时主持人打开了剩下两扇门中的一扇，后面是一只山羊（这里有个隐含前提：主持人是知道门后的情况的）。主持人问你，要不要换另一扇仍然关闭着的门，还是就要你刚才选中的那扇。

那么问题就是，换另一扇门会增加你赢得汽车的概率么？换与不换的概率各是多少呢？

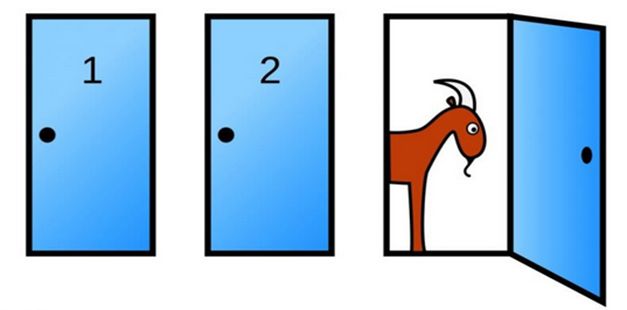
因为只剩下了两扇门，其中有一车和一羊，因此答案是换不换概率都是1/2，对么？

也有人坚信不换的概率是1/3，那么换的概率就应该是2/3？无论哪种回答，一定都会有自己的解释和逻辑。

 

什么是概率？无非就是某种事件发生的可能性。

如何验证概率？只有用大量的实验来统计各种事件发生的分布情况。

放到现实中，想看到这个问题的答案，只能由主持人和观众不断的重复进行游戏。

看看比如说各自100次游戏，不换门会选中多少次，换门又会选中多少次。

 

这就体现出了代码的优势，无需舞台无需观众无需主持人，也无需一遍又一遍的重复。

让我们直接抛开语义和逻辑上的争论，让事实来说话。

 

完全忠实于游戏的规则来实现：

 1 import random

 2 import logging

 3 

 4 class MontyHall(object):

 5     def __init__(self, num=3):

 6         '''

 7         创建一个door列表

 8         0表示门关闭的状态

 9         1表示该门后有车

10         -1表示该门被主持人打开

11         '''

12         self.doors = [0] * num

13         self.doors[0] = 1

14         self.choice = -1

15         self.shuffle()

16 

17     def shuffle(self):

18         '''

19         开始新的游戏

20         关闭所有打开的门（-1）

21         重新安排轿车的位置

22         '''

23         for i in range(len(self.doors)):

24             if self.doors[i] == -1:

25                 self.doors[i] = 0

26         random.shuffle(self.doors)

27 

28     def makeChoice(self):

29         '''

30         player随机选择一扇门

31         '''

32         self.choice = random.randint(0, len(self.doors)-1)

33         logging.info('choice: %d' % self.choice)

34         logging.info('original: %s' % self.doors)

35 

36     def excludeChoice(self):

37         '''

38         主持人排除选择

39         直到只剩两扇门

40         '''

41         toBeExcluded = []

42         for i in range(len(self.doors)):

43             if self.doors[i] == 0 and i != self.choice:

44                 toBeExcluded.append(i)

45 

46         random.shuffle(toBeExcluded)

47         for i in range(len(self.doors)-2):

48             self.doors[toBeExcluded[i]] = -1

49         logging.info('final: %s' % self.doors)

50 

51     def changeChoice(self):

52         '''

53         player改变选择

54         '''

55         toChange = []

56         for i in range(len(self.doors)):

57             if i != self.choice and self.doors[i] != -1:

58                 toChange.append(i)

59         self.choice = random.choice(toChange)                

60         logging.info('choice changed: %d' % self.choice)

61 

62     def showAnswer(self):

63         logging.info(self.doors)

64 

65     def checkResult(self):

66         gotIt = False

67         if self.doors[self.choice] == 1:

68             gotIt = True

69         return gotIt

 

不改变选择：

 1 def test(n):

 2     result = {}

 3     game = MontyHall()

 4 

 5     for i in range(n):

 6         game.shuffle()

 7         game.makeChoice()

 8         game.excludeChoice()

 9 

10         if game.checkResult():

11             result['yes'] = result.get('yes', 0) + 1

12         else:

13             result['no'] = result.get('no', 0) + 1

14 

15     for key in result:

16         print('%s: %d' % (key, result[key]))

17     

18 

19 

20 if __name__ == '__main__':

21     logging.basicConfig(format='%(levelname)s:%(message)s', level=logging.WARNING)

22     test(10000)

View Code

yes: 3304

no: 6696

 

改变选择：

 1 def test(n):

 2     result = {}

 3     game = MontyHall(3)

 4 

 5     for i in range(n):

 6         game.shuffle()

 7         game.makeChoice()

 8         game.excludeChoice()

 9         # 改变选择

10         game.changeChoice()

11 

12         if game.checkResult():

13             result['yes'] = result.get('yes', 0) + 1

14         else:

15             result['no'] = result.get('no', 0) + 1

16 

17     for key in result:

18         print('%s: %d' % (key, result[key]))

19     

20 

21 

22 if __name__ == '__main__':

23     logging.basicConfig(format='%(levelname)s:%(message)s', level=logging.WARNING)

24     test(10000)

View Code

yes: 6691

no: 3309

 

可见，如果不改变，选中的概率是1/3。如果改变，选中概率为2/3。所以说，最佳策略是换门。

 

从逻辑上如何解释呢？

如果你每次都换，只有当你第一次选的那扇门后是汽车时，你才会输。

因为第一次选中汽车的概率是1/3，所以换门后输的概率是1/3。

也就是说，如果你每次都换，赢的概率就有2/3。

 

还不信么？

那我们换成50扇门再做这个游戏。你选一扇门，我把其他是羊的48扇门打开给你，最后依然剩下两扇门，你还会觉得换和不换的概率一样是1/2么？

依然觉得在50扇门中任选一个，最后中将的概率是1/2？

 

 

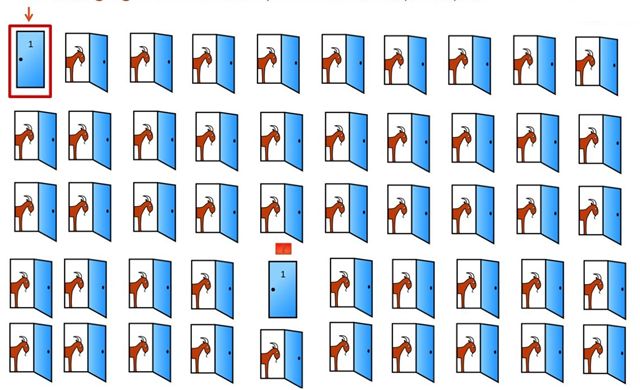
原理是一样的，只有你第一次就选中汽车时（1/50概率），换门才会失去大奖。其他的情况，换门都会让你赢得大奖，概率为49/50。

再次用代码来验证：

 1 def test(n):

 2     result = {}

 3     game = MontyHall(50)

 4 

 5     for i in range(n):

 6         game.shuffle()

 7         game.makeChoice()

 8         game.excludeChoice()

 9         game.changeChoice()

10 

11         if game.checkResult():

12             result['yes'] = result.get('yes', 0) + 1

13         else:

14             result['no'] = result.get('no', 0) + 1

15 

16     for key in result:

17         print('%s: %d' % (key, result[key]))

18     

19 

20 

21 if __name__ == '__main__':

22     logging.basicConfig(format='%(levelname)s:%(message)s', level=logging.WARNING)

23     test(10000)

View Code

yes: 9794

no: 206

 

依然不相信？

逻辑分析和事实数据都不能让你相信？还是认为最后的概率都是1/2？

那我只好遗憾的表示，三门问题的答案是确定的，不存在任何争议。

自己去科普一下吧，不要困在自己的局限的认知里。

 

附上一个科普节目，让大名鼎鼎的流言终结者（S09E21）来扫盲吧。

 

如果逻辑分析+实验事实+科普节目都无法让你放弃1/2的结论，那我真无能为力了：）