吴恩达机器学习(五)神经网络 2/2 —— 反向传播算法(BP-神经网络)
本章目录
- 1. 为什么要用反向传播——梯度下降
- 2. 反向传播的基础补充——链式法则
- 3. 反向传播是什么——直观展示
-
- 3.1 前向传播过程回顾
- 3.2 反向传播过程展示
- 3.3 小结
- 4. 公式推导
-
- 4.1 误差计算 —— δ \delta δ
- 4.2 梯度计算——误差矩阵 Δ Δ Δ
- 4.3 梯度矩阵—— D D D
- 5. 反向传播计算过程总结
- 6. 补充:权值随机初始化
1. 为什么要用反向传播——梯度下降
上一篇中我们构建了神经网络模型,并推导出其代价函数(见 2.3代价函数),那么可以像逻辑回归那样利用梯度下降来优化参数吗?
跟之前一样,梯度下降法也是通过求 J ( θ ) J(\theta) J(θ) 的偏导数来更新参数,对于某个 θ i j \theta_{ij} θij,给它加上减去一个很小的量 ϵ 来计算梯度:
∂ J ( θ ) ∂ θ j ≈ J ( θ 1 , ⋯ , θ j + ϵ , ⋯ , θ n ) − J ( θ 1 , ⋯ , θ j − ϵ , ⋯ , θ n ) 2 ϵ \frac{\partial J(\theta)}{\partial\theta_j} \approx \frac{J(\theta_1,\cdots,\theta_j+\epsilon,\cdots,\theta_n)-J(\theta_1,\cdots,\theta_j-\epsilon,\cdots,\theta_n)}{2\epsilon} ∂θj∂J(θ)≈2ϵJ(θ1,⋯,θj+ϵ,⋯,θn)−J(θ1,⋯,θj−ϵ,⋯,θn)但稍微分析一下算法的复杂度就能知道,这样的方法计算速度十分缓慢。对于每一组数据,我们需要计算所有权值的梯度: 总 的 计 算 次 数 = 训 练 样 本 个 数 ∗ 网 络 权 值 个 数 ∗ 前 向 传 播 计 算 次 数 总的计算次数 = 训练样本个数 * 网络权值个数 * 前向传播计算次数 总的计算次数=训练样本个数∗网络权值个数∗前向传播计算次数在通常情况下这样的计算复杂度是无法接受的,因此我们需要引入反向传播算法来简化计算。
2. 反向传播的基础补充——链式法则
为了能够理解之后对于 反向传播 公式的推导,我们首先要了解一个关于 多元复合函数求导的 链式法则。下图中, x , y x,y x,y 是自变量, u , v u,v u,v 是 x , y x,y x,y 的函数, p , q p,q p,q 又是 u , v u,v u,v 的函数,最后 z z z 是 p , q p,q p,q 的函数:
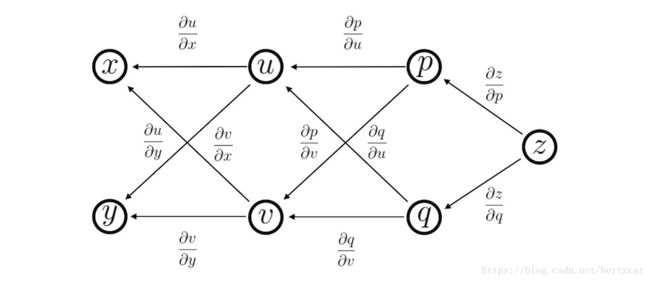
当我们要求 z z z对 x , y x,y x,y的偏导数,有以下公式:
∂ z ∂ x = ∂ z ∂ p ∂ p ∂ u ∂ u ∂ x + ∂ z ∂ p ∂ p ∂ v ∂ v ∂ x + ∂ z ∂ q ∂ q ∂ u ∂ u ∂ x + ∂ z ∂ q ∂ q ∂ v ∂ v ∂ x \frac{\partial z}{\partial x} = \frac{\partial z}{\partial p} \frac{\partial p}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial p} \frac{\partial p}{\partial v} \frac{\partial v}{\partial x} + \frac{\partial z}{\partial q} \frac{\partial q}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial q} \frac{\partial q}{\partial v} \frac{\partial v}{\partial x} ∂x∂z=∂p∂z∂u∂p∂x∂u+∂p∂z∂v∂p∂x∂v+∂q∂z∂u∂q∂x∂u+∂q∂z∂v∂q∂x∂v ∂ z ∂ y = ∂ z ∂ p ∂ p ∂ u ∂ u ∂ y + ∂ z ∂ p ∂ p ∂ v ∂ v ∂ y + ∂ z ∂ q ∂ q ∂ u ∂ u ∂ y + ∂ z ∂ q ∂ q ∂ v ∂ v ∂ y \frac{\partial z}{\partial y} = \frac{\partial z}{\partial p} \frac{\partial p}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial z}{\partial p} \frac{\partial p}{\partial v} \frac{\partial v}{\partial y} + \frac{\partial z}{\partial q} \frac{\partial q}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial z}{\partial q} \frac{\partial q}{\partial v} \frac{\partial v}{\partial y} ∂y∂z=∂p∂z∂u∂p∂y∂u+∂p∂z∂v∂p∂y∂v+∂q∂z∂u∂q∂y∂u+∂q∂z∂v∂q∂y∂v和上图类似,神经网络就是一个有很多层次的多元函数。
3. 反向传播是什么——直观展示
注:下图均是以一个样本为例计算,并不是整个训练集
3.1 前向传播过程回顾
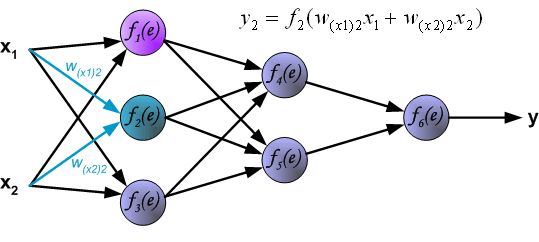
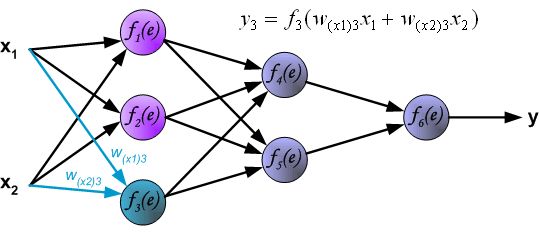
首先以一个两输入、一输出的四层神经网络为例回顾下 前向传播(Forward Propagation)的过程:(图源)
注意:其中 f ( e ) f(e) f(e)为激活函数, w w w表示权重参数,为保持符号统一,后续还是用 θ \theta θ表示
- 第一层为输入层,输入信号为 x 1 , x 2 x_1,x_2 x1,x2,
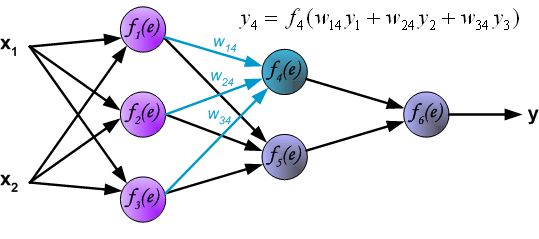
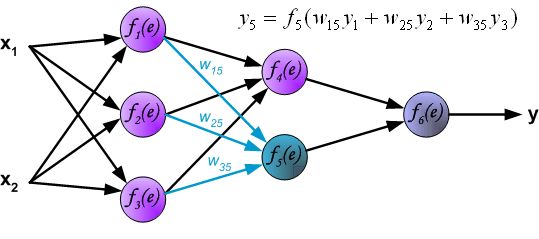
最后一层是输出层:
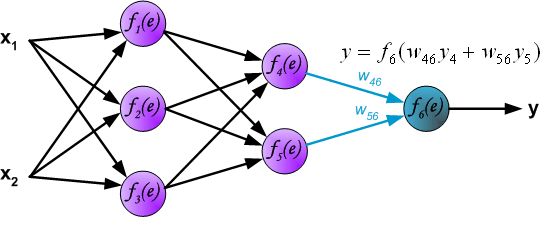
到这里为止,神经网络的一轮前向传播已经完成,最后输出的 y y y 就是本次前向传播神经网络计算出来的结果(预测结果),但这个预测结果不一定是正确的,和真实的标签 z z z 相比较,预测结果存在误差 δ δ δ,如下:
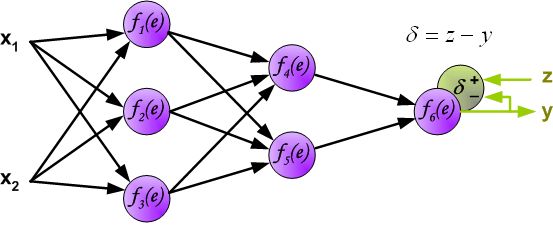
我们知道,优化一个神经网络就是优化它的权重(参数),最开始已经解释了用普通方法计算的复杂度,因此就有了反向传播的基本思路:
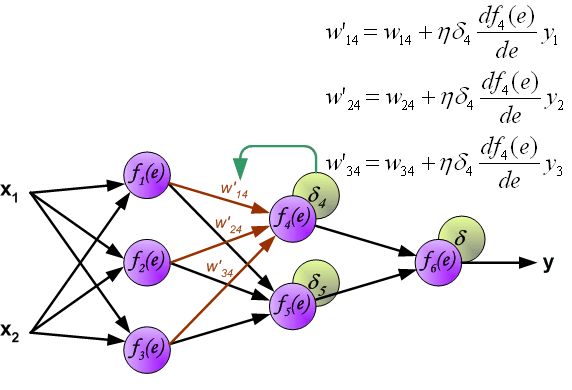
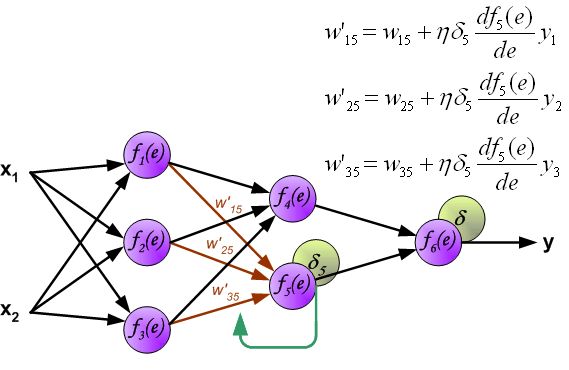
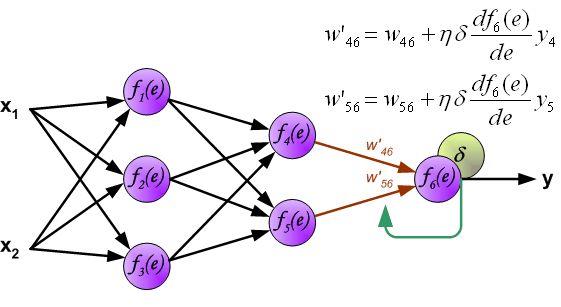
3.2 反向传播过程展示
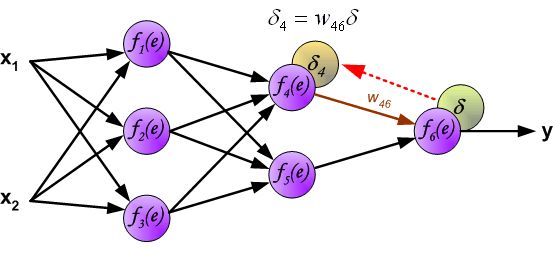
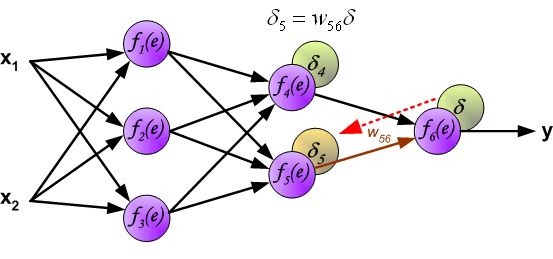
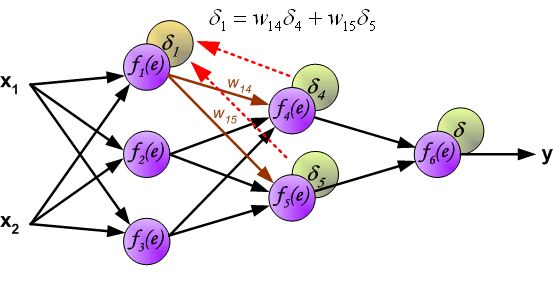
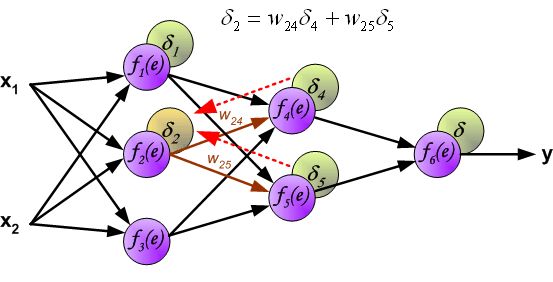
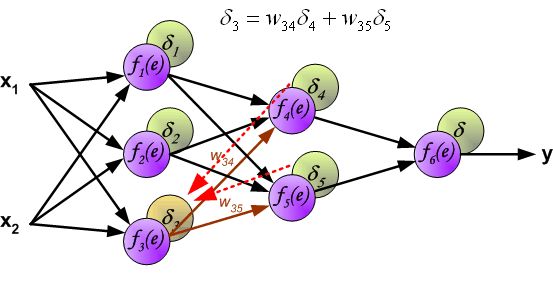
输出层神经元有其对应的真实标签,可以想象内部的隐藏层神经元也有其对应的真实标签,只是我们看不到也无法计算,但我们可以用反向传播误差的思想来计算内部神经元与其真实值之间的误差。
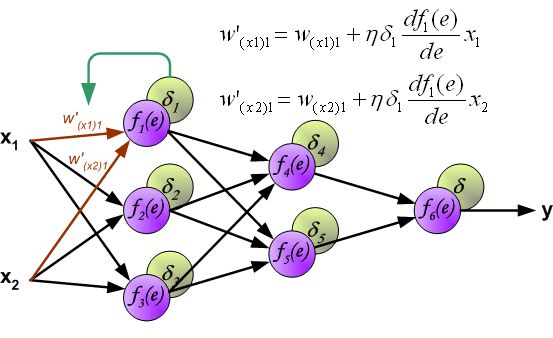
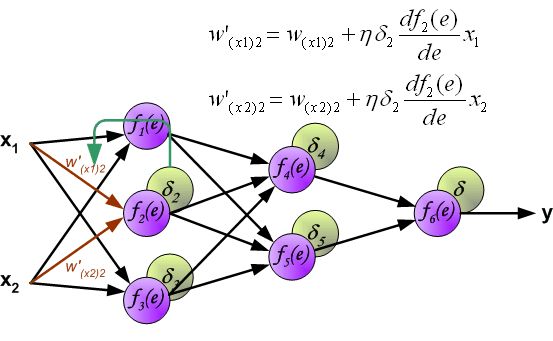
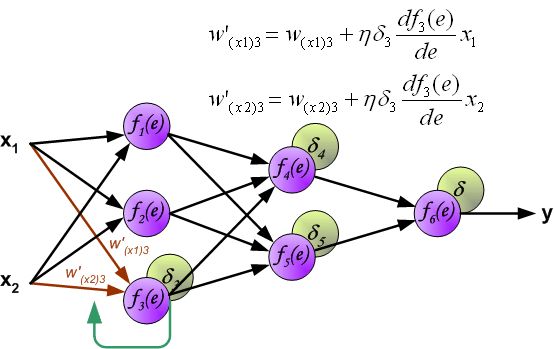
- 改变数据流的方向,通过层与层之间的权重,可以得到每个神经元的误差 δ i δ_i δi:
3.3 小结
由上述过程,我们可以明确两点:
- 正向传播——求损失,即代价函数
- 反向传播——回传误差,得到梯度,更新权重
4. 公式推导
在之前的逻辑回归和线性回归中,梯度下降法可以表示为:
θ : = θ − α ∂ J ( θ ) ∂ θ \theta:=\theta-\alpha\frac{\partial J(\theta)}{\partial \theta} θ:=θ−α∂θ∂J(θ)而在神经网络中,我们使用反向传播得到的误差 δ \delta δ 来获取梯度 ∂ J ( θ ) ∂ θ \frac{\partial J(\theta)}{\partial \theta} ∂θ∂J(θ)
4.1 误差计算 —— δ \delta δ
以下面4层神经网络为例:

定义 第 l l l 层第 j j j 个神经元的误差 为(其中 z z z是上图中的中间变量): δ j ( l ) = ∂ J ( θ ) ∂ z j ( l ) \delta_j^{(l)}=\frac{\partial J(\theta)}{\partial z_j^{(l)}} δj(l)=∂zj(l)∂J(θ)可以简化为 第 l l l 层神经元的误差 是: δ ( l ) = ∂ J ( θ ) ∂ z ( l ) , z ( l ) = θ ( l − 1 ) a ( l − 1 ) \delta^{(l)}=\frac{\partial J(\theta)}{\partial z^{(l)}}\ ,\ z^{(l)}=\theta^{(l-1)}a^{(l-1)} δ(l)=∂z(l)∂J(θ) , z(l)=θ(l−1)a(l−1)对误差公式的解释如下(参考: 如何理解反向传播的误差公式):
分析网络的内部,稍微把 z ( l ) z^{(l)} z(l) 改一下,就会影响到神经网络 h θ ( x ) h_θ(x) hθ(x) 的值,从而影响到 J ( θ ) J(θ) J(θ)。
因此 ∂ J ( θ ) ∂ z ( l ) \displaystyle \frac{\partial J(\theta)}{\partial z^{(l)}} ∂z(l)∂J(θ)表示神经元的加权输入 z ( l ) z^{(l)} z(l)的变化给损失函数 J ( θ ) J(\theta) J(θ)带来的变化梯度。
如果神经网络符合数据,根据最小值条件(函数取得最小值的必要条件,导数为0),变化率应该为0。那就是说,可以认为 δ ( l ) \delta^{(l)} δ(l)表示与神经网络符合数据的理想状态的偏差。这个偏差表示为“误差”。
下面我们就来算一下各层的误差 δ \delta δ:
- Layer4: δ ( 4 ) = a ( 4 ) − y \delta^{(4)}=a^{(4)}-y δ(4)=a(4)−y
- Layer3(链式求导): δ ( 3 ) = ∂ J ∂ z ( 3 ) = ∂ J ∂ a ( 4 ) ⋅ ∂ a ( 4 ) ∂ z ( 4 ) ⋅ ∂ z ( 4 ) ∂ a ( 3 ) ⋅ ∂ a ( 3 ) ∂ z ( 3 ) = ( − y a ( 4 ) + 1 − y 1 − a ( 4 ) ) ⋅ [ a ( 4 ) ( 1 − a ( 4 ) ) ] ⋅ θ ( 3 ) ⋅ [ a ( 3 ) ( 1 − a ( 3 ) ) ] = ( a ( 4 ) − y ) ⋅ θ ( 3 ) ⋅ g ′ ( z ( 3 ) ) = ( θ ( 3 ) ) T ⋅ δ ( 4 ) ⋅ g ′ ( z ( 3 ) ) ( 吴 恩 达 给 出 的 顺 序 , 具 体 应 用 以 实 际 维 度 为 准 ) \begin{aligned}\delta^{(3)}=\frac{\partial J}{\partial z^{(3)}} &=\frac{\partial J}{\partial a^{(4)}}\ ·\ \frac{\partial a^{(4)}}{\partial z^{(4)}}\ ·\ \frac{\partial z^{(4)}}{\partial a^{(3)}}\ ·\ \frac{\partial a^{(3)}}{\partial z^{(3)}}\\ \\ &=(\frac{-y}{a^{(4)}}+\frac{1-y}{1-a^{(4)}})\ ·\ [a^{(4)}(1-a^{(4)})]\ ·\ \theta^{(3)}\ ·\ [a^{(3)} (1-a^{(3)})]\\ \\ &=(a^{(4)}-y)\ ·\ \theta^{(3)}\ ·\ g'(z^{(3)})\\\\ &=(\theta^{(3)})^T\ ·\ \delta^{(4)}\ ·\ g'(z^{(3)}) \ \ \ (吴恩达给出的顺序,具体应用以实际维度为准) \end{aligned} δ(3)=∂z(3)∂J=∂a(4)∂J ⋅ ∂z(4)∂a(4) ⋅ ∂a(3)∂z(4) ⋅ ∂z(3)∂a(3)=(a(4)−y+1−a(4)1−y) ⋅ [a(4)(1−a(4))] ⋅ θ(3) ⋅ [a(3)(1−a(3))]=(a(4)−y) ⋅ θ(3) ⋅ g′(z(3))=(θ(3))T ⋅ δ(4) ⋅ g′(z(3)) (吴恩达给出的顺序,具体应用以实际维度为准)
将代价函数简化表示为: J ( θ ) = − y log h ( x ) − ( 1 − y ) log ( 1 − h ( x ) ) = − y log a ( 4 ) − ( 1 − y ) log ( 1 − a ( 4 ) ) J(\theta)=-y\log h(x)-(1-y)\log (1-h(x))=-y\log a^{(4)} -(1-y)\log (1-a^{(4)}) J(θ)=−ylogh(x)−(1−y)log(1−h(x))=−yloga(4)−(1−y)log(1−a(4)),所以:
∂ J ∂ a ( 4 ) = ( − y a ( 4 ) + 1 − y 1 − a ( 4 ) ) \frac{\partial J}{\partial a^{(4)}}=(\frac{-y}{a^{(4)}}+\frac{1-y}{1-a^{(4)}}) ∂a(4)∂J=(a(4)−y+1−a(4)1−y)Sigmoid函数的导数为: g ′ ( z ) = g ( z ) ( 1 − g ( z ) ) g'(z)=g(z)(1-g(z)) g′(z)=g(z)(1−g(z)),所以:
∂ a ( 4 ) ∂ z ( 4 ) = ∂ g ( z ( 4 ) ) ∂ z ( 4 ) = a ( 4 ) ( 1 − a ( 4 ) ) \frac{\partial a^{(4)}}{\partial z^{(4)}}=\frac{\partial g(z^{(4)})}{\partial z^{(4)}}=a^{(4)}(1-a^{(4)}) ∂z(4)∂a(4)=∂z(4)∂g(z(4))=a(4)(1−a(4)) ∂ a ( 3 ) ∂ z ( 3 ) = ∂ g ( z ( 3 ) ) ∂ z ( 3 ) = a ( 3 ) ( 1 − a ( 3 ) ) \frac{\partial a^{(3)}}{\partial z^{(3)}}=\frac{\partial g(z^{(3)})}{\partial z^{(3)}}=a^{(3)}(1-a^{(3)}) ∂z(3)∂a(3)=∂z(3)∂g(z(3))=a(3)(1−a(3))
- Layer2(推导同上): δ ( 2 ) = ∂ J ∂ z ( 2 ) = ( θ ( 2 ) ) T ⋅ δ ( 3 ) ⋅ g ′ ( z ( 2 ) ) \delta^{(2)}=\frac{\partial J}{\partial z^{(2)}}=(\theta^{(2)})^T\ ·\ \delta^{(3)}\ ·\ g'(z^{(2)}) δ(2)=∂z(2)∂J=(θ(2))T ⋅ δ(3) ⋅ g′(z(2))
4.2 梯度计算——误差矩阵 Δ Δ Δ
在上一步计算得到每一层神经元的误差后,就可以计算每层 θ \theta θ 的梯度,用误差矩阵 Δ Δ Δ 表示(注:以下的 J ( θ ) J(\theta) J(θ)无正则化): Δ ( 3 ) = ∂ J ∂ θ ( 3 ) = ∂ J ∂ z ( 4 ) ⋅ ∂ z ( 4 ) ∂ θ ( 3 ) = δ ( 4 ) ( a ( 3 ) ) T Δ^{(3)}=\frac{\partial J}{\partial \theta^{(3)}}= \frac{\partial J}{\partial z^{(4)}}\ ·\ \frac{\partial z^{(4)}}{\partial \theta^{(3)}} =\delta^{(4)} (a^{(3)})^T Δ(3)=∂θ(3)∂J=∂z(4)∂J ⋅ ∂θ(3)∂z(4)=δ(4)(a(3))T Δ ( 2 ) = ∂ J ∂ θ ( 2 ) = ∂ J ∂ z ( 3 ) ⋅ ∂ z ( 3 ) ∂ θ ( 2 ) = δ ( 3 ) ( a ( 2 ) ) T Δ^{(2)}=\frac{\partial J}{\partial \theta^{(2)}}= \frac{\partial J}{\partial z^{(3)}}\ ·\ \frac{\partial z^{(3)}}{\partial \theta^{(2)}} =\delta^{(3)} (a^{(2)})^T Δ(2)=∂θ(2)∂J=∂z(3)∂J ⋅ ∂θ(2)∂z(3)=δ(3)(a(2))T Δ ( 1 ) = ∂ J ∂ θ ( 1 ) = ∂ J ∂ z ( 2 ) ⋅ ∂ z ( 2 ) ∂ θ ( 1 ) = δ ( 2 ) ( a ( 1 ) ) T Δ^{(1)}=\frac{\partial J}{\partial \theta^{(1)}}= \frac{\partial J}{\partial z^{(2)}}\ ·\ \frac{\partial z^{(2)}}{\partial \theta^{(1)}} =\delta^{(2)} (a^{(1)})^T Δ(1)=∂θ(1)∂J=∂z(2)∂J ⋅ ∂θ(1)∂z(2)=δ(2)(a(1))T一般化为:
Δ ( l ) = ∂ J ∂ θ ( l ) = δ ( l + 1 ) ( a ( l ) ) T Δ^{(l)}=\frac{\partial J}{\partial \theta^{(l)}}=\delta^{(l+1)}(a^{(l)})^T Δ(l)=∂θ(l)∂J=δ(l+1)(a(l))T
加上下标:
Δ i j ( l ) = ∂ J ∂ θ i j ( l ) = a j ( l ) δ i ( l + 1 ) Δ_{ij}^{(l)}=\frac{\partial J}{\partial \theta_{ij}^{(l)}}=a_j^{(l)}\delta_i^{(l+1)} Δij(l)=∂θij(l)∂J=aj(l)δi(l+1)
- l l l :代表目前所计算的是第几层
- j j j :代表目前计算层中的激活单元的下标
- i i i :代表下一层中误差单元的下标
4.3 梯度矩阵—— D D D
加上正则化项和系数 1 m \frac{1}{m} m1,用 D ( l ) D^{(l)} D(l) 来表示每层权值 θ ( l ) \theta^{(l)} θ(l) 的更新过程: θ ( l ) : = θ ( l ) + α D ( l ) \theta^{(l)}:=\theta{(l)}+\alpha D^{(l)} θ(l):=θ(l)+αD(l)其中 D i j ( l ) = { 1 m Δ i j ( l ) + λ m θ i j ( l ) if j ≠ 0 1 m Δ i j ( l ) if j = 0 D_{ij}^{(l)}= \begin{cases} \displaystyle\frac{1}{m}Δ_{ij}^{(l)}+\frac{\lambda}{m}\theta_{ij}^{(l)}\ \ & \text{if $j≠0$} \\ \\ \displaystyle\frac{1}{m}Δ_{ij}^{(l)} & \text{if $j=0$ } \end{cases} Dij(l)=⎩⎪⎪⎪⎨⎪⎪⎪⎧m1Δij(l)+mλθij(l) m1Δij(l)if j=0if j=0
5. 反向传播计算过程总结
- 初始化所有神经元的误差,即对于所有的 l , i , j l,i,j l,i,j,初始化 Δ i j ( l ) = 0 Δ_{ij}^{(l)}=0 Δij(l)=0
- 对于 m m m 个样本中的每一个样本:
- 获取输入变量 a ( 1 ) = x ( k ) , k = 1 , 2 ⋅ ⋅ ⋅ , m a^{(1)}=x^{(k)},k=1,2···,m a(1)=x(k),k=1,2⋅⋅⋅,m
- 前向传播,计算各层激活向量 a ( l ) a^{(l)} a(l)
- 计算输出层误差 δ ( L ) \delta^{(L)} δ(L)
- 计算其他层误差 δ ( L − 1 ) , δ ( L − 2 ) , . . . , δ ( 2 ) \delta^{(L-1)}, \delta^{(L-2)},...,\delta^{(2)} δ(L−1),δ(L−2),...,δ(2)
- 计算误差矩阵 Δ i j ( l ) : = Δ i j ( l ) + a j ( l ) δ i ( l + 1 ) Δ_{ij}^{(l)}:=Δ_{ij}^{(l)}+a_j^{(l)}\delta_i^{(l+1)} Δij(l):=Δij(l)+aj(l)δi(l+1)
- 计算梯度矩阵: D i j ( l ) = { 1 m Δ i j ( l ) + λ m θ i j ( l ) if j ≠ 0 1 m Δ i j ( l ) if j = 0 D_{ij}^{(l)}= \begin{cases} \displaystyle\frac{1}{m}Δ_{ij}^{(l)}+\frac{\lambda}{m}\theta_{ij}^{(l)}\ \ & \text{if $j≠0$} \\ \\ \displaystyle\frac{1}{m}Δ_{ij}^{(l)} & \text{if $j=0$ } \end{cases} Dij(l)=⎩⎪⎪⎪⎨⎪⎪⎪⎧m1Δij(l)+mλθij(l) m1Δij(l)if j=0if j=0
- 更新权值: θ ( l ) : = θ ( l ) + α D ( l ) \theta^{(l)}:=\theta^{(l)}+\alpha D^{(l)} θ(l):=θ(l)+αD(l)
6. 补充:权值随机初始化
对于逻辑回归,通常将参数初始化为0。对于神经网络,初始化为0不可行。
如果我们令所有的初始参数都为0或者一个非0的数,这会导致每层的 激活单元 都相同,每一层都在计算相同特征,那么是无法进行非线性的拟合的。换句话说,本来我们希望不同的神经元学习到不同的特征,但是由于参数相同以及输出值都一样,不同的结点根本无法学到不同的特征!这样就失去了网络学习特征的意义了。
因此我们使用随机化的初始化方法,通常将参数初始化为 ( − ε , ε ) (−ε,ε) (−ε,ε)之间的随机值。
参考:
1.反向传播过程
2.带下标的公式推导
3.不带下标的公式推导
4.吴恩达机器学习笔记week5