算法5-初级算法数组-旋转数组-存在重复元素-只出现一次的数-两个数组的交集-加一-移动零-有效的数独
初级算法-旋转数据
需求
给你一个数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
示例2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
注意:
| 2022/4/27 |
|---|
| leecode此案例中不需要将数组输出,需要的是把nums数组替换成修改好的即可。 |
测试代码在:package offer2.Test426;
所有可运行代码都在leecode
方法1:使用额外字符串
public void rotate(int[] nums, int k) {
// 创建一个新的数组用于存放右旋后的数据
int[] array = new int[nums.length];
// 使用for循环 实现数据的右旋k位
for(int i = 0; i<nums.length ; i++){
// 新数组元素 与 旧数组元素 下标之间的关系是: newcode = (oldcode + k) % n
array[(i + k )%nums.length] = nums[i];
}
System.arrayCopy(array,0,nums,0,nums.length);
}
时间复杂度:O(n),因为使用了循环,其中n是数组的长度。
空间复杂度:O(n),因为新建了一个数组,n表示新建数组的长度。
图示分析:
![]()
知识准备
System类的方法
| 方法 | 说明 |
|---|---|
| static void arraycopy(Object src,int srcPos,Object dest,int destPos,int length) | 将指定源数组中的数组从指定位置复制到目标数组的指定位置 |
方法2:不使用额外数组(环状替换)
public void rotate(int[] nums, int k) {
// 获取数组长度
int n = nums.length;
// 对k进行取余操作,为了减少遍历时间,因为对于n个数来说,
// 如果右旋次数超过n次,相当于整个数组又进行了一次循环。
k = k % n;
// 统计循环次数,不太清楚到底是什么内容?
int count = method(k,n);
// 使用for循环
for(int start = 0; start < count ;start ++){
int prev = nums[start];
int current = start;
do{
int next = (current + k ) % n;
int temp = nums[next];
nums[next] = prev;
prev = temp;
current = next;
}while(start != current);
}
}
public int method(int x,int y){
return y>0?method(y,x%y):x;
}
时间复杂度:O(n),每个元素只会遍历一次,n为数组长度;
空间复杂度:O(1),只需要常量空间存放若干变量。
method方法理解图示:

n和k的最大公约数等于1,1次遍历就可以完成交换,比如:7-3,7-4,4-3
n和k的最大公约数不等于1,1次遍历是无法完成所有元素归位的,需要m(最大公约数)次,比如:4-2,最大公约数是2
问题:
当数组长度是nums.length 与 k 有公因子。
方法3:多次翻转数组
public void rotate(int[] nums,int k){
int len = nums.length;
k = k % n ;
method(0,len-1,nums);
method(0,k-1,nums);
method(k,len-1,nums);
}
// 数组的翻转
public void method(int x,int y,int[] nums){
for(int i = x,j = y ;i<= j ; i++,j--){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
分析:
多次翻转:原始是1,2,3,4,5,6,7
翻转一次: 7,6,5,4,3,2,1
翻转二次: 5,6,7,4,3,2,1
翻转三次: 5,6,,7,1,2,3,4
时间复杂度:O(n),数组元素被翻转了2次,一个有n个元素,因此是O(2n) = O(n)
空间复杂度:O(1),因为只是用了一个len常量保存数组长度。
方式4:数组复制
public void rotate(int[] nums,int k){
int n = nums.length;
k = k % n;
// 使用Arrays.copyOfRange、copyOf 方法
int[] start = Arrays.copyOfRange(nums,n-k,len);
int[] end = Arrays.copyOf(nums,n-k);
// 使用System.arraycopy 方法
System.arraycopy(start,0,nums,0,start.length);
System.arraycopy(end,0,nums,start.length,end.length);
}
知识准备
Arrays类的方法
| 方法 | 说明 |
|---|---|
| public static < T > T[] copyOfRange(T[] original,int from,int to) | 将指定数组的指定范围复制到新数组中 |
| public static boolean[] copyOf(boolean[] original,int newLength) | 复制指定的数组,截断或填充false |
初级算法-存在重复元素
需求
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
方法1:暴力解法
public boolean containsDuplicate(int[] nums) {
for(int i = 0 ; i < nums.length-1 ; i++){
for(int j = i+1; j < nums.length; j++){
if(nums[i] == nums[j]){
return true;
}
}
}
return false;
}
方法2:set集合
public boolean containsDuplicate(int[] nums) {
HashSet<Integer> set = new HashSet<Integer>();
for(int i = 0; i< nums.length; i++){
if(!set.add(nums[i])) {
return true;
}
}
return false;
}
方法3:数组排序Arrays.sort()
public boolean containsDuplicate(int[] nums) {
Arrays.sort(nums);
for(int i = 0; i< nums.length-1;i++){
if(nums[i] == nums[i+1]){
return true;
}
}
return false;
}
初级算法-只出现一次的数
需求
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
示例:
输入: [2,2,1],输出: 1
输入: [4,1,2,1,2],输出: 4
方式1:暴力解法(双重for循环)
思路:每一元素都和别的元素进行比较,包括它自己。
public int singleNumber(int[] nums) {
// 如果数组长度是1,说明只有一个元素。
if(nums.length == 1){
return nums[0];
}
// 定义变量用于做返回值。
int result = 0;
for(int i = 0; i< nums.length;i++){
// 定义变量,用于统计元素的个数
int count = 0 ;
for(int j = 0 ; j < nums.length;j++){
if(nums[i] == nums[j]){
count++;
}
}
// 判断count,如果为1,说明该元素只有一个
if(count == 1){
result = nums[i];
}
}
return result;
}
时间复杂度:O(n),两层for循环,经历时间应该是O(2n),当量级还是O(n)
空间复杂度:O(1),定义了两个变量,占用固定的空间,说明是是常数量级。
方式2:异或形式
思路:使用异或的形式,将所有的数字进行异或处理,只出现一次的数会被保留下来。
a ^ a = 0 任何数和自己本身异或 结果是0
a ^ 0 = a 任何数字和0异或等于它自己
a ^ b ^ c = a ^ c ^ b 异或满足交换律
// 增强for循环
public int singleNumber(int[] nums) {
int result = 0;
for(int a :nums){
result = result ^ a;
}
return result;
}
// 普通for循环
public int singleNumber(int[] nums) {
int result = 0;
for(int i = 0;i<nums.length;i++){
result ^= nums[i];
}
return result;
}
// 减少result变量
public int singleNumber(int[] nums) {
for(int i = 1 ; i < nums.length ; i++){
nums[0] ^= nums[i];
}
return nums[0];
}
方式3:使用Set集合 add remove toArray方法
所使用的方法:
| 方法名 | 说明 |
|---|---|
| boolean add(E e) | 确保此集合包含指定的元素 |
| boolean remove(Object o ) | 从该集合中删除指定元素的单个实例 |
| object[] toArray() | 返回一个包含此集合中所有元素的数组 |
public int singleNumber(int[] nums) {
HashSet<Integer> set = new HashSet<Integer>();
for(int a : nums){
if(!set.add(a)){
set.remove(a);
}
}
return (int)set.toArray()[0];
}
方式4:使用排序Arrays.sort()
public int singleNumber(int[] nums) {
Arrays.sort(nums);
for(int i = 0 ; i < nums.length ; i++){
// 因为涉及到两次i++操作,所以i最后需要停在nums.length-2的位置
if((i < nums.length-1) && (nums[i] == nums[i+1])){
i++;
}else return nums[i];
}
return nums[nums.length-1];
}
初级算法-两个数组的交集
需求
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
示例:
输入:nums1 = [1,2,2,1], nums2 = [2,2] 输出:[2,2]
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4] 输出:[4,9]
方法1:对数组进行排序 + 双指针 + 集合 + 数组
public int[] intersect(int[] nums1, int[] nums2) {
// 对数组进行排序
Arrays.sort(nums1);
Arrays.sort(nums2);
// 定义集合存储两个数组的交集,
// 使用集合的原因是 不知道两个数组中交集元素的个数,故不能直接使用数组存储,数组是定长的
List<Integer> list = new ArrayList<Integer>();
// 定义两个指针,用于遍历两个数组
int i = 0,j=0;
// 使用while循环,进入循环的条件是 索引没有超出任何一个数组的长度
while(i < nums1.length && j < nums2.length){
// 两个数组的元素相等 则存储到list集合中
if(nums1[i] == nums2[j]){
list.add(nums1[i]);
i++;
j++;
// 当元素 数组1 》 数组2 则将数组2的索引向后移动
}else if(nums1[i] > nums2[j]){
j++;
// 当元素 数组1 《 数组2 则将数组1的索引向后移动
}else if(nums1[i] < nums2[j]){
i++;
}
}
// 创建数组存储 给定数组的交集
int[] array = new int[list.size()];
i = 0;
// 增强for循环遍历集合存储到数组中。
for(Integer a : list){
array[i++] = a;
}
return array;
}
方法2:map集合(数组元素,个数) + 集合 + 数组
public int[] intersect(int[] nums1, int[] nums2) {
// 创建集合用于存储 两个数组的交集
List<Integer> list = new ArrayList<Integer>();
// 创建Map集合,存储元素元素及出现次数
Map<Integer,Integer> map = new HashMap<Integer,Integer>();
for(int i = 0; i < nums1.length ; i++){
Integer key = nums1[i];
Integer value = map.get(key);
// 如果key已经在集合中,则修改value的值,再将键值对存储到map中
if(map.containsKey(key)){
value ++;
map.put(key,value);
// key不在集合中,将键值堆(key,1)存入集合中
}else{
map.put(key,1);
}
}
// 遍历数组2
for(int i = 0 ; i< nums2.length ;i++){
Integer key = nums2[i];
Integer value = map.get(key);
// 判断数组2中的元素是否在集合中 并且对应的值是否大于0,
// 满足 = 将key添加到list集合中,修改value值,在将键值对放入map中
if(map.containsKey(key) && value > 0 ){
list.add(key);
value--;
map.put(key,value);
}
}
// 遍历list集合 将元素存储到数组中。
int[] array = new int[list.size()];
for(int i = 0; i< array.length ;i++){
array[i] = list.get(i);
}
return array;
}
方法3:Arrays的sort、copyofRange双指针数组
public int[] intersect(int[] nums1, int[] nums2) {
// 获得两个数组中的最小值,创建数组
int len1 = nums1.length;
int len2 = nums2.length;
int len = len1 > len2? len1:len2;
// 对两个数组进行排序
Arrays.sort(nums1);
Arrays.sort(nums2);
// 创建新数组 存放给定数组的交集
int[] array = new int[len];
int i= 0, j =0 , k =0;
// 使用双指针 比较
while(i < len1 && j < len2){
if(nums1[i] == nums2[j]){
array[k++] = nums1[i];
i++;
j++;
}else if(nums1[i] > nums2[j]){
j++;
}else{
i++;
}
}
return Arrays.copyOfRange(array,0,k);
}
方法4:Arrays的sort、copyofRange + 双指针
public int[] intersect(int[] nums1,int[] nums2){
int len1 = nums1.length;
int len2 = nums2.length;
// 指针k表示 数组交集组成数组的长度
int i = 0,j =0,k =0;
// 对数组进行排序
Arrays.sort(nums1);
Arrays.sort(nums2);
// 使用双指针
while( i < len1 && j < len2){
// 数组1 和 数组2 相同的时候,且 i != k的时候 num1[i] 和 num1[k] 交换
if(nums1[i] == nums2[j]){
if(i != k ){
int temp = nums1[k];
nums1[k] = nums1[i];
nums1[i] = temp;
}
k++;
i++;
j++;
}else if(nums1[i] > nums2[j]){
j++;
}else{
i++;
}
}
return Arrays.copyOfRange(nums1,0,k);
}
图示:
初级算法-加一
需求
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
案例:
输入:digits = [1,2,3] ;输出:[1,2,4]
输入:digits = [4,3,2,1] ;输出:[4,3,2,2]
输入:digits = [0] ;输出:[1]
方法1:数组遍历
public int[] plusOne(int[] digits) {
// 数组长度
int len = digits.length;
// 遍历数组,从后开始,因为加1操作线程个位开始
for(int i = len-1;i >= 0; i--){
// 不等于9 直接+1返回即可
if(digits[i] != 9){
digits[i]++;
return digits;
// 等于9的 加1涉及到进位问题,所以需要赋值为0,然后继续处理前一位
}else{
digits[i] = 0;
}
}
// 如果遍历所有元素都没有返回digits,
//说明数组中的内容全是9,则需要新建数组,长度是原来数组长度+1
int[] newarray = new int[len+1];
// 给新数组第一个元素赋值为1,其余元素是0,因为数组初始化时元素都是0
newarray[0] = 1;
return newarray;
}
图示:
![]()
方法2:数组遍历 + 覆盖数组
public int[] plusOne(int[] digits) {
for(int i = digits.length-1 ; i>= 0 ; i--){
if(digits[i] != 9){
digits[i]++;
return digits;
}else{
digits[i] = 0;
}
}
digits = new int[digits.length+1];
digits[0] = 1;
return digits;
}
对比方法1,减少了内存占用情况。
移动零
需求
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例:
输入: nums = [0,1,0,3,12] ;输出: [1,3,12,0,0]
输入: nums = [0] ;输出: [0]
方法1:双指针 (非零往前移,剩余补0)
遍历数组 非零数移动位置
public void moveZeroes(int[] nums) {
int i = 0 ,j = 0;
for(; i < nums.length;i++){
if(nums[i] != 0){
nums[j] = nums[i];
j++;
}
}
while(j<nums.length){
nums[j] = 0;
j++;
}
for(i = j; i <nums.length;i++){
nums[i] = 0;
}
}
最后的遍历采用while循环:内存占用是42.5M,时间是1ms
最后的遍历采用for循环:内存占用是42.9M,时间是1ms
图示:

方法2:双指针 (非零元素移动到0的位置)
关键点是:nums[j-i] = nums[j] 这个情况是怎么想到的。
指针i 表示0的个数;
指针j 用于遍历数组;
public void moveZeroes(int[] nums){
int i = 0;
for(int j = 0 ; j < nums.length ; j++){
if(nums[j] == 0){
i++;
}else if(i != 0){
nums[j-i] = nums[j];
nums[j] = 0;
}
}
}
方法3:双指针(非零元素与0元素交换)
public void moveZeroes(int[] nums) {
int leftZero = 0; // 存储的是最左侧的0元素的下标
int countZero = 0; // 存储的是0元素的个数
for(int i = 0 ; i< nums.length ; i++){
if(nums[i] == 0){
if(countZero == 0){
leftZero = i;
countZero = 1;
}else countZero++;
}else{
if(countZero != 0){
nums[leftZero++] = nums[i];
nums[i] = 0;
}
}
}
}
nums[leftZero] = nums[i];
leftZero++;
时间是:2ms,内存消耗是:42.5M。
nums[leftZero++] = nums[i];
时间是:1ms,内存消耗是:42.8M。
有效的数独
需求
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
示例图示:

方法1:两层循环遍历
思路:二维数组 存放行、列、3*3正方块元素;
多个二维数组分别存放 行 、 列 、以及每个九宫格的元素 是否存在的标识,存在就数组值=1;不存在数组值=0;
public boolean isValidSudoku(char board[][]) {
// 字符数组长度 char类型 但存储的是
int length = board.length;
//二维数组line表示的是对应的行中是否有对应的数字,比如line[0][3]
//表示的是第0行(实际上是第1行,因为数组的下标是从0开始的)是否有数字4
int line[][] = new int[length][length];
int column[][] = new int[length][length];
int cell[][] = new int[length][length];
for (int i = 0; i < length; ++i)
for (int j = 0; j < length; ++j) {
//如果还没有填数字,直接跳过
if (board[i][j] == '.')
continue;
// -'0' 将字符数组中的字符元素 变成 数字,
// - 1 操作的原因是:由于定义的数组长度是9 那么索引是0-8 但是数独中的数字是1-9
// 将 num = 9 放在数组索引的位置,那么会出现问题,所以将数独中的1-9 置换成 0-8
int num = board[i][j] - '0' - 1;
//k是第几个单元格,9宫格数独横着和竖着都是3个单元格
// i/ 3 表示该元素属于第几行的3*3九宫格,j/3 表示该元素是第几列的3*3的九宫格;
// 假设(i,j)=(4,5),则说明该单元格属于编号为4的九宫格,实际上就是第5个九宫格
int k = i / 3 * 3 + j / 3;
//如果当前数字对应的行和列以及九宫格,只要一个由数字,说明冲突了,直接返回false。
//举个例子,如果line[i][num]不等于0,说明第i(i从0开始,实际上就是i+1)行有 num+1 这个数字。
// 因为cell中的索引num存储的是 数独中的元素-1 的值
if (line[i][num] != 0 || column[j][num] != 0 || cell[k][num] != 0)
return false;
// 表示第i行有num这个数字,第j列有num这个数字,对应的单元格内也有num这个数字
// 二维数组的值置为1
line[i][num] = column[j][num] = cell[k][num] = 1;
}
return true;
}
用时:1ms;内存:41.4M
方法2:位运算解决
思路:采用int类型的数值 表示1-9之间的数字是否存在,存在位置=1,不存在位置是=0
public boolean isValidSudoku(char[][] board) {
// 定义三个int类型的数组,长度是9 存放行、列、九宫格 内容
// 举例行,则第一行的元素存储在 line[0] 中
int[] line = new int[9];
int[] column = new int[9];
int[] cell = new int[9];
//
int shift = 0;
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
//如果还没有填数字,直接跳过
if (board[i][j] == '.')
continue;
// board[i][j] - '0' 将字符类型 变成 数值类型
// 且整体数组的元素 中低10位表示 存储的1-9 数字是否存在。
// 存在就将1 向左移动几位。
shift = 1 << (board[i][j] - '0');
// 第k+1个九宫格
int k = (i / 3) * 3 + j / 3;
//如果对应的位置只要有一个大于0,说明有冲突,直接返回false
if ((column[i] & shift) > 0 || (line[j] & shift) > 0 || (cell[k] & shift) > 0)
return false;
// 将shift中的1 添加到三个数组中。
column[i] |= shift;
line[j] |= shift;
cell[k] |= shift;
}
}
return true;
}
方法3:使用集合
思路:使用Set集合不能存储相同元素的性质去 判断行、列、九宫格是否有重复元素。
public boolean isValidSudoku(char[][] board) {
for(int i = 0;i < 9;i++){
HashSet setLine = new HashSet();
HashSet setCol = new HashSet();
HashSet setBox = new HashSet();
for (int j = 0; j < 9; j++) {
// 利用set集合不能存储相同元素的性质判断行、列、九宫格是否有重复元素
if(board[i][j] != '.' &&!setLine.add(board[i][j])){
return false;
}
if(board[j][i] != '.' && !setCol.add(board[j][i])){
return false;
}
int a = i / 3 * 3 + j/3;
int b = i % 3 * 3 + j % 3 ;
if(board[a][b] != '.' && !setBox.add(board[a][b])){
return false;
}
}
}
return true;
}
时间:2ms;内存:41.4M。
旋转图像
需求
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
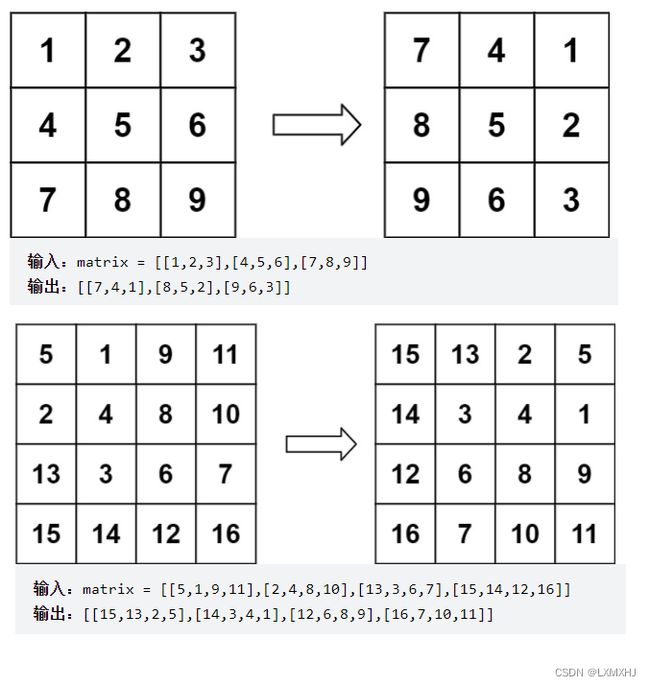
方法1:先上下换再对角线换
关键点:
public void rotate(int[][] matrix) {
// 二维数组的行数
int lenX = matrix.length;
// 二维数组的列数
int lenY = matrix.length;
// 定义变量用于数据交换
int temp = 0;
// 根据行对称进行交换
for(int i = 0 , j = lenX-1 ; i < j ; i ++,j--){
for(int k = 0 ; k < lenY ; k ++){
temp = matrix[i][k];
matrix[i][k] = matrix[j][k];
matrix[j][k] = temp;
}
}
// 按照对角线 交换元素
for(int i = 0 ; i < lenX ; i++){
for(int j = i+1 ; j < lenY ; j++){
temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
}
时间:0ms;内存40M;
方法2:直接进行旋转
-
案例代码过程:

-
代码:
public void rotate(int[][] matrix) {
//矩阵行、列数量
int len = matrix.length;
int m = 0;
int n = 0;
int temp = 0;
// 对于外层循环遍历一半就行 原因未知
for(int i = 0; i < len /2 ; i ++){
for(int j = i ; j < len -i-1; j++){
m = len - j - 1;
n = len - i - 1;
temp = matrix[i][j];
matrix[i][j] = matrix[m][i];
matrix[m][i] = matrix[n][m];
matrix[n][m] = matrix[j][n];
matrix[j][n] = temp;
}
}
}
方法3:矩阵转置(对角线交换) + 列首尾互换
代码:
public void rotate(int[][] matrix) {
int len = matrix.length;
int temp = 0;
for(int i = 0 ; i < len ; i++){
for(int j = i+1 ; j < len ; j++){
temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
for(int i = 0 , j = len-1 ; i < j ; i++,j--){
for(int k = 0; k < len; k++){
temp = matrix[k][i];
matrix[k][i] = matrix[k][j];
matrix[k][j] = temp;
}
}
}