插入排序-希尔排序-选择排序-冒泡排序-快速排序-基数排序-外部排序-归并排序[数据结构与算法]

    大三党，大数据专业，正在为面试准备，欢迎学习交流。
    文章详细总结了插入排序、希尔排序、选择排序、归并排序、交换排序（冒泡排序、快速排序）、基数排序、外部排序。从思想到代码实现。

往期文章
绪论-数据结构的基本概念
绪论-算法
线性表-顺序表和链式表概念及其代码实现
查找-顺序+折半+索引+哈希

1 排序的基本概念

1.1 何为排序

    将一组数据元素序列重新排列，使得数据元素序列按某个数据项（关键字）有序。

1.2 稳定排序和不稳定排序

    对于任意的数据元素序列，若排序前后所有相同关键字的相对位置都不变，则称该排序方法称为稳定的排序方法。
    若存在一组数据序列，在排序前后，相同关键字的相对位置
发生了变化，则称该排序方法称为不稳定的排序方法。

1.3 内部排序和外部排序

    若整个排序过程不需要访问外存便能完成，则称此类排序问题为内部排序；

    反之，若参加排序的记录数量很大，整个序列的排序过程不可能在内存中 完成，则称此类排序问题为外部排序。

2 插入排序

2.1 基本思想

2.2 插入排序三步曲

定位->挤空->插入

• 在R[1…i-1]中查找R[i]的插入位置，
  R[1…j].key  R[i].key < R[j+1…i-1].key；
• 将R[j+1…i-1]中的所有记录均后移 一个位置；
• 将R[i] 插入(复制)到R[j+1]的位置上

2.3 举例

排序过程：整个排序过程为n-1趟插入，即先将序列中第
1个记录看成是一个有序子序列，然后从第2个记录开始，
逐个进行插入，直至整个序列有序

2.4 算法的代码描述

• 两层循环外层控制无序序列的取值 内层控制岗哨在有序的排序 找到位置跳出插入
• r[0] 作为岗哨 每次从无序依次取出放入 用来和有序序列比较插入
• j控制有序序列 j=i-1 每次都从有序的最后一个开始
• i控制无序序列 从前往后取 和 j顺序相反
• 代码中从小到大排序
• 需要注意第二个循环如果岗哨比所有的值都要小最后会r[0] 和r[0]自己比较一样能够跳出循环

补充 重要 岗哨的目的也是为了防止覆盖 可以思考 如果先移动有序序列就会把无序序列的第一个值覆盖

typedef struct
{ int key;//关键字
  float info;//该成员的其他信息
}JD;

void straisort(JD r[],int n)//对长度为n的序列
{
 int i,j;
 for(i=2;i<=n;i++)
 {
  r[0]=r[i]//第一个需要排序的设为岗哨 不取因为1看做有序 其余n-1看做无序序列 
  j=i-1;//从后往前
  //需要注意第二个循环如果岗哨比所有的值都要小最后会r[0] 和r[0]自己比较一样能够跳出循环
  while(r[0].key<r[j].key)
  {
     r[j+1]=r[j]
     j--;
  }
  r[j+1]=r[0]
 }
}

2.5 时间复杂度

最好情况分析：如果n个值比较。开始1个为有序 n-1为无序。需要进行n-1趟的排序。当序列为初始就是顺序排列。那么每次取出放入岗哨的值都比有序的大，那么每趟只需要比较一次。比较次数为n-1。由于需要放入岗哨再移动到有序的最后所以每趟移动2次。
最坏情况分析：当序列为初始就是逆序排列。一样是n-1趟排序，第1趟比较次数为2（特别注意 岗哨除了跟第一个值比较 还要跟自己比较一次才能跳出循环 回头看代码 ）所以应该是 2,3,4…n 等差数列相加。第1趟移动为3次（1是移动到岗哨 2是有序值后移 3 是岗哨移到有序值之前的位置）所以应该是 3,3,4…n+1 等差数列相加

2.6 性能总结+改进直接插入的方法

简单插入排序的本质比较和交换
简单插入排序复杂度由逆序个数决定
如何改进简单插入排序复杂度?

• 分组，比如C(n,2)/2>2C((n/2),2)/2
• 3,2,1有3组逆序对(3,1)（3,2）(2,1)需要交换3次。但相隔较远的3,1交换一次后1,2,3就没有逆序对了。
• 基本有序的插入排序算法复杂度接近O(n)

3 希尔排序（插入排序的改进方法）

3.1 基本思想

    分割成若干个较小的子文件，对各个子文件分别进行直接插入排序，当文件达到基本有序时，再对整个文件进行一次直接插入排序。

对待排记录序列先作“宏观”调整，再作“微观”调整

3.2 排序过程

1. 首先将记录序列分成若干子序列，
2. 然后分别对每个子序列进行直接插入排序，
3. 最后待基本有序时，再进行一次直接插入排序

如下
其中，d 称为增量，它的值在排序过程中从大到小逐渐缩小，直至最后一趟排序减
为 1。

3.3 数值演示

记住思想，若干个部分有序最后达到整体有序，使得复杂度最低。

3.4 算法的代码描述

注意看注释，特别注意d[ ]是什么
1三个循环嵌套
2最外循环控制选择不同的d
3二层循环控制依次取出间隔为d的两个值，比较后后移一位
4最内层循环控制 2个值之间的比较换位置

//r[]表示待排序的序列 n表示个数 
//d[]表示增量序列 就是d的取值 7 6 5 ..这样
// T表示几种增量序列  d[]的元素个数   
void shellsort(JD r[],int
n,int d[]，int T)
 { 
   int i,j,k;
   JD x;
   k=0;
 //循环每一趟进行分组，组内进行简单插入排序
 }

while(k<T)
{
  for(i=d[k]+1;i<=n;i++)
 //i为未排序记录的位置
 {
  x=r[i];
  //每组两个数 位置为 i j j为本组i前面的记录位置
  j=i-d[k];
  while((j>0)&&(x.key<r[j].key))
 //组内简单插入排序
  { 
    r[j+d[k]]=r[j];
    j=j-d[k];
  }
 r[j+d[k]]=x;
 }
 k++;
}

3.5 希尔排序特点

• 子序列的构成不是简单的“逐段分割”，而是将相隔某个增量的记录组成一个子序列
• 希尔排序可提高排序速度，因为(分组后n值减小，n²更小，而T(n)=O(n²),所以T(n)从总体上看是减小了)(关键字较小的记录跳跃式前移，在进行最后一趟增量为1的插入排序时，序列已基本有序)
• 增量序列取法(无除1以外的公因子)(最后一个增量值必须为1)

3.6 最坏时间复杂度分析及总结

【定理】使用希尔增量的最坏时间复杂度为 o( N2 ).
如下例子

希尔排序算法本身很简单，但复杂度分析很复杂. 他适合于中等数据量大小的排序（成千上万的数据量）.

4 选择排序

4.1 基本思想

    从无序子序列中“选择”关键字最小或最大的记录，并将它加入到有序子序列中，以此方法增加记录的有序子序列的长度。

4.2 排序过程

1. 首先通过n-1次关键字比较，从n个记录中找出关键字最小的记录，将它与第一个记录交换
2. 再通过n-2次比较，从剩余的n-1个记录中找出关键字次小的记录，将它与第二个记录交换
3. 重复上述操作，共进行n-1趟排序后，排序结束

4.3 算法的代码描述

两层循环

外层循环控制每次比较的序列从n 到n-1 …2 每次减去1（也可以理解成初始坐标从 1 到n-1 逐渐后移）

内层循环找到最小值的坐标

然后交换每趟第一个值和最小值的位置（只变换两个）

void smp_selesort(JD r[], int n){
	int i, j, k;
	JD x;
	for (i = 1;i<n;i++){
		k = i;//初始把每趟第一个坐标设为最小关键字坐标
		//循环找到未排序的最小关键字下标
		for (j = i + 1;j <= n;j++)
		{
			if (r[j].key<r[k].key) 
				k = j;
		}
		//如果最小坐标不是原来的 交换
		if (i != k)
		{
			x = r[i];
			r[i] = r[k];
			r[k] = x;
		}
	}

4.4 算法性能分析（复杂度）

• 若n个记录，需要n-1趟。当2个值需要比较1次 3个值比较2次 n个值比较n-1次。等差数列求和得到总次数。
• 当序列顺序不需要移动
• 当序列逆序，每趟需要移动3次。如下代码
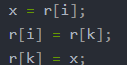
• 由于需要额外的一个空间所以复杂度为常数1，就是上面的x

总结如下

补充-稳定性分析

5 归并排序

5.1 基本思想

归并——将两个或两个以上的有序表组合成一个新的有序表，叫归并排序

5.2 二路归并排序流程

设初始序列含有n个记录，则可看成n个有序的子序列，每个子序列长度为1两两合并，得到【n/2】个长度为2或1的有序子序列再两两合并，……如此重复，直至得到一个长度为n的有序序列为止

5.3 算法描述

待补充

5.4 算法评价

6 交换排序

通过“交换”无序序列中的记录从而得到其中关键字
最小或最大的记录，并将它加入到有序子序列中，以此方法增加记录的有序子序列的长度。

• 冒泡排序（简单）
• 快速排序（复杂）

6.1 冒泡排序（简单）

6.1.21排序过程

1. 将第一个记录的关键字与第二个记录的关键字进行比 较，若为逆序r[1].key>r[2].key，则交换；然后比较第二个记录与第三个记录；依次类推，直至第n-1个 记录和第n个记录比较为止——第一趟冒泡排序，结果关键字最大的记录被安置在最后一个记录上
2. 对前n-1个记录进行第二趟冒泡排序，结果使关键字 次大的记录被安置在第n-1个记录位置
3. 重复上述过程，直到“在一趟排序过程中没有进行过 交换记录的操作”为止
   

6.1.2算法的实现

两层循环

外层循环控制排序的序列长度 从前n个 到 前n-1个 …前2个

内层循环控制前后两个数两两比较及交换位置。下标1 和 2 ；2 和 3；…

注意这边设置flat标志位 如果一层外层循环中没有交换 那么直接退出外层循环

void bubble_sort(JD r[], int n)
{
	int m, i, j, flag = 1;
	JD x;
	m = n ;
	while ((m>1) && (flag == 1))/*趟数*/
	{
		flag = 0;/*本趟是否有交换操作标识初始化*/
		for (j = 1;j < m;j++)//*本趟将最大元素放到为排序序列的最后*/
			if (r[j].key>r[j + 1].key)
			{
				flag = 1;
				x = r[j];
				r[j] = r[j + 1];
				r[j + 1] = x;
			}
			m--;
	}
}

6.1.3算法评价（复杂度）

最坏情况一样用等差序列的计算 n-1趟 每趟的值逐渐减小1
交换用到一个额外的空间 所以空间复杂度为1

6.1.4 冒泡排序的改进(关键)

• 冒泡排序的结束条件为，最后一趟没有进行“交换记录”。
• 一般情况下，每经过一趟“冒泡”，“m减1”，但并不是每趟都如此。

只需要一个变量指向最后一次交换的位置。作为下一次的m

6.2 快速排序（复杂）

6.2.1 基本思想

选择一个枢纽，把其他的元素分为两个不相交的两个集合A1 A2。A1中的元素全部都小于枢纽，A2中的元素全部都大于枢纽。 同样的对A1,A2也这样处理，如此反复。

结束条件,个数小于2。

6.2.2 枢纽的选择

6.2.3 排序过程

1. 对r[s……t]中记录进行一趟快速排序，附设两个指针i和j，设划分元记录rp=r[s]，x=rp.key
2. 初始时令i=s,j=t
3. 首先从j所指位置向前搜索第一个关键字小于x 的记录，并和rp交换
4. 再从i所指位置起向后搜索，找到第一个关键字大于x的记录，和rp交换
5. 重复上述两步，直至i==j为止
6. 再分别对两个子序列进行快速排序，直到每个子序列只含有一个记录为止

6.2.4 算法的实现

嵌套的两个while比较难理解，嵌套中其实并没有交换，只是把值覆盖枢纽位置的值，枢纽并没有更换过来。当外循环结束再把枢纽填入到中间位置。此时i=j。

例如初始值 如下 枢纽为10 亮的位置是枢纽的现在位置 代码中实际变化如下

10(i) 8 11 7(j) --》 10比7大 7覆盖10的位置（枢纽的位置） 并没有马上更换原本7为10（也就是没有马上更换枢纽的现在位置）

7 8(i) 11 7(j) --》i后移一个到8比10小 不变

7 8 11(i) 7(j) --》i后移一个到11比10大 11覆盖7的位置（枢纽的位置）

7 8 11(i j) 11 --》i=j结束
7 8 10 11 --》 退出外while循环 把枢纽填入

void qksort(JD r[], int t, int w)
{//t=low,w=high
	int i, j, k;//i j表示两个移动的坐标（指针）（头和尾）
	JD x;
	if (t >= w) return;//结束条件
	i = t; j = w; x = r[i]; //赋值操作 同时把第一个值作为枢纽x
	while (i<j)
	{
		while ((i<j) && (r[j].key >= x.key)) j--;//枢轴后面的值大于枢轴
			if (i<j) { r[i] = r[j]; i++; }//当不满足时，与枢轴交换
			while ((i<j) && (r[i].key <= x.key)) i++;//枢轴前面的值小于枢轴
				if (i<j) { r[j] = r[i]; j--; }//不满足，与枢轴交换
	}
	r[i] = x;
	qksort(r, t, j - 1);
	qksort(r, j + 1, w);
}

6.2.5 性能评价（复杂度）

待补充这部分（空间的不是很明白）

6.2.6 快速排序算法特点

• 快速排序算法是不稳定的–对待排序序列 49 49’ 38 65，快速排序结果为: 38 49’ 49
  65
• 快速排序的性能跟初始序列中关键字的排列和选取的枢纽有关
• 当初始序列按关键字有序(正序或逆序)时，性能最差，蜕化为冒泡排序，时间复杂度为O(n2）
• 常用“三者取中”法来选取划分记录，即取首记录r[s].key.尾记录r[t].key和中间记录r[(s+t)/2].key三者的中间值为划分记录。
• 快速排序算法的平均时间复杂度为O(nlogn)

7 基数排序

7.1 基数排序定义

7.2 高位优先多关键字排序

先对K0进行排序，并按 K0 的不同值将记录序列分成若干子序列之后，分别对 K1 进行排序，……， 依次类推，直至对最次位关键字Kd-1排序完成为止。

7.3 低位优先多关键字排序

首先按关键字 Kd-1进行排序，然后按关键字Kd-2进行排序，……，依次类推，直最后对最主位关键字K0排序完成为止。

7.4 链式基数排序操作

        例如三位整数，百位优先级>十位优先级>个位优先级。取值0~9。我们可以给出10个桶如下，每个桶都有头指针节点和尾指针节点，当我们采用低位优先可以将数据根据个位数放入到对应的桶子中，相同桶子数据依次穿成链表。当数据全部放入我们从第一个桶子开始，每一个尾指针指向下一个非空桶的头指针节点。最后拉直，完成。
        由于有三个关键字需要进行3趟，具体实现如下图。

7.5 顺序存储结构实现链式基数排序

类似的原理，我们可以设置头指针和尾指针，但是需要注意的是 f[] e[] 分别记录的是第一个数据的坐标和最后一个数据的坐标。而不是指针。

8 外部排序

8.1 外部排序的基本概念

大多数内排序算法都是利用了内存是直接访问的事实,读写一个数据是常量的时间。如果输入是在磁带上，磁带上的元素只能顺序访问。甚至数据是在磁盘上，效率还是下降，因为转动磁盘和移动磁头会产生延迟。

8.2 外排序模型

• 外排序具有设备依赖性。这里考虑的算法工作在磁带上
• 完成有效的排序至少需要两个磁带机
• 三个磁带机可以简化问题
• 外排序由两个阶段组成：预处理阶段 归并阶段

8.3 预处理阶段

概述：根据内存的大小将一个有n个记录的文件分批读入内存，用各种内排序算法排序，形成一个个有序片段。

• 最简单的方法是按照内存的容量尽可能多地读入数据记录，然后在内存进行排序，排序的结果写入文件，形成一个已排序片段。
• 每次读入的记录数越小，形成的初始的已排序片段越多。而已排序片段越多，归并的次数也越多。
• 如果能够让每个初始的已排序片段包含更多的记录，就能减少排序时间。置换选择可以让我们在只能容纳p个记录的内存中生成平均长度为2p的初始的已排序片段。

置换选择

• 如何更有效地构造已排序片段
• 事实上，只要第一个元素被写到输出磁带上，它所用的内存空间就可以给别的元素使用。如果输入磁带上的下一个元素比刚刚输出的元素大，它能被放入这个已排序片段。

置换选择流程(看下图很容易理解)

• 初始时，将M个元素读入内存，用一个优先队列存储这M个元素。
• 执行一次取最小元素操作，把最小的元素写入输出磁带。
• 从输入磁带读入下一个元素。
  • 1如果它比刚才写出去的元素大，则把它加入到优先级队列；
  • 2.否则，它不可能进入当前的已排序片段。因为优先级队列比以前少了一个元素，该元素就被放于优先级队列的空余位置，
• 继续这个过程，直到优先级队列的大小为0，此时该已排序片段结束。我们重新构建一个优先级队列，开始了一个新的已排序片段，此时用了所有存放在空余位置中的元素。
  置换选择实例演示流程
  

8.4 归并阶段之两路归并

文字描述可能比较复杂配合看图的实例演示比较容易

• 假设我们有四条磁带A1,A2,B1和B2，两个用于输入，两个用于输出。开始时数据在A1上

• 内存一次能排序M个记录

• 工作流程

  • 1 从输入磁带上一次读入M个记录，对它们进行内排序，然后把已排序片段轮流写到B1和B2。回绕所有的磁带 。–预处理

  • 2 取每条磁带上的第一个已排序片段，把它们归并起来，并把结果写到A1。然后，从每条磁带上取下一个已排序片段，把它们归并起来，结果写到A2。继续这个过程，轮流把结果写到A1和A2，

  • 3 回绕四条磁带，重复同样的步骤，这次使用A磁带作为输入，而B磁带作为输出。

  • 4 重复步骤二和三，直到剩下一个长度为N的已排序片断

实例演示如下

1. 每次读入3个到内存，排序后全部输出到B1。第二次再读入3个到内存排序输出到B2，第三次输出到B1如此反复。

2. 每次B1三个值和B2三个值归并输入到A1，下一次输入到A2如此反复和上面一样。

3. 同理，A1 A2作为输出，每次各取6个归并输入到B1，下一次输入到B2，如此反复

4. 最后B1 B2作为输入 ，B1取12个 B2取出仅剩的一个归并输出到A1,结束。
   
   
   
   
   
   时间分析
   

8.5 归并阶段之多路归并

如果还有额外的磁带，则可以用多路归并（multiwaymerge）或K路归并（K-way merge）来减少排序输入数据所需要的归并处理次数。 与两路归并原理一致



时间效益

内容较多，如果有遗漏和错误的地方，欢迎指出。