2022深圳杯C题思路模型
自动驾驶电动物料车换电站选址及调度方案
为了实现我国在2030年前“碳达峰”、在2060年前“碳中和”的目标,在物料运输中使用环保的自动驾驶电动车是发展趋势。点击获取更多完整思路代码
在制订电动车调度方案时,必须考虑充、换电池的时间成本,从而提出了新的车辆运输选址及调度问题。
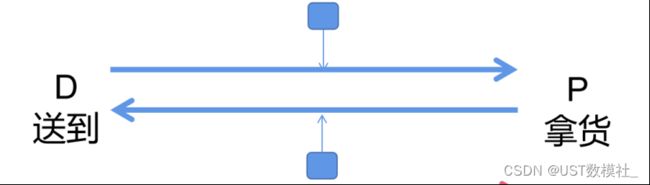
问题1 一批自动驾驶电动物料车将物料从P点运送到D点,然后空载返回,如此循环往复运送物料。要求建立数学规划模型,在P点与D点之间确定一个双向同址(像高速的休息站一样)的换电站位置,以及对应的车辆和电池组调度方案,极大化指定时间段内运送物料量,满足资源约束与电池运行方式约束。根据附录所给的数据,求解规划模型,给出换电站位置,并给出在1000小时中运送的物料量,所使用车辆、电池组数量和车辆及其各电池组的具体调度方案。
问题一思路:
问题需要我们求出具体的选址以及调度方案,所以学习过数学建模模型的同学应该可以很快地反应,我们需要用到规划模型,从文中所给我们可以得到决策变量:换电站的位置,根据到P点以及D点的距离,来得出我们的规划模型;
目标函数: 运输的趟数最多或者可以说,到达D点的次数最多 。接下来的约束条件, 只需要根据调度方案选择合适的出发点就可以了。看起来, 出发点的选择可以靠近点P, 又恰好让车跑到90%时更换电池。
我们给出第一问的部分代码供大家参考,后续持续更新!
import numpy as np
from itertools import product
class Lorry:
def __init__(self, station1, station2):
# station1: P->D 换电站位置, station2:D->P 换电站位置
self.bet = 100 # 当前电池电量
self.p = 20 - station2 # 当前位置
self.t = 0 # 当前时间
self.station1 = station1
self.station2 = station2
self.n_charge = 0 # 充电次数
def __str__(self):
return "Lorry is at position {}, with battery {}, at time {}".format(self.p, self.bet, self.t)
def move(self, dt):
# 0(P)___10(D)___20(P')
# dt时间后的演化结果
if 0 <= self.p < 10 or np.isclose(self.p, 0):
# P->D
self.bet -= 1/2 * dt # 电池消耗
elif 10 <= self.p < 20 or np.isclose(self.p, 10):
# D->P
self.bet -= 1/3 * dt # 电池消耗
if self.bet < 0 or np.isclose(self.bet, 0):
raise Exception("Lorry is out of battery")
self.t = self.t + dt # 时间变化
self.p = (self.p + dt * 1) % 20 # 位置变化
if np.isclose(self.p, 10) or np.isclose(self.p, 0):
# 装卸货时间
self.t += 1
self.recharge()
def recharge(self):
if (np.isclose(self.p, self.station1) or np.isclose(self.p, 20 - self.station2)) and 10 <= self.bet <= 12.6:
# 逐渐降低阈值,测试是否存在可行解
self.bet = 100
# print("Lorry is recharged at time {}".format(self.t))
# gap.append(self.t)
# print(self)
self.t += 2
self.n_charge += 1
# for (sta1, sta2) in product(np.arange(0, 10, 1), np.arange(0, 10, 1)):
for sta1 in np.arange(0.1, 10, 0.1):
sta2 = sta1
lorry = Lorry(sta1, sta2)
try:
for T in range(1000*60*10):
lorry.move(dt=0.1)
print('({:.1f}, {:.1f}) worked with charge {:d} times'.format(sta1, sta2, lorry.n_charge))
except Exception as e:
print((sta1, sta2), e, end='\r')
# # gap = []
# (sta1, sta2) = (5, 5)
# lorry = Lorry(sta1, sta2)
# for T in range(1000*60*10):
# lorry.move(dt=0.1)
# # print(lorry.n_charge)
# # gap = [gap[i] - gap[i-1] for i in range(1, len(gap))]
# # gap = np.array(gap)
# # print(gap.min())
# n_lorry = 75
具体换车换电流程为:
初始时, 有75辆车运行, 50辆满电的车备用.
将所有车按1-75进行编号, 初始时, 以0.2km间隔发车, 则最后一辆车与第一辆车有约为5km的间隔.
在满载的状态下, 若如果路过换电站时, 电量在10%至12.6%, 只选择换电, 不选择换车.
在空载的状态下, 若如果路过换电站时, 电量在10%至12.6%, 按照如下状态进行换车换电:
第一轮位于空载状态下路过换电站, 对1-50车进行换车操作, 50-75号车进行换电操作, 则75号与1号车间隔缩小(但仍远大于0.2km), 50号与51号车间隔变大.
第二轮位于空载状态下路过换电站, 对51-75, 1-25车进行换车操作, 25-75号车进行换电操作
第三轮位于空载状态下路过换电站, 对25,-75车进行换车操作, 1-25号车进行换电操作
三轮操作为一个循环, 间距回到原来的状态.
持续更新!关注UST数模社