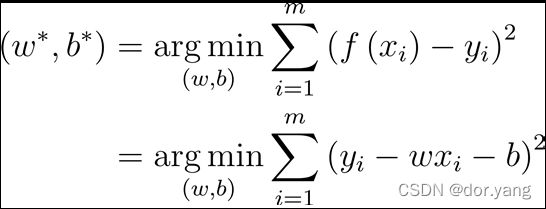机器学习实验报告1——线性模型,决策树,神经网络部分
机器学习前三次实验报告
1.线性模型
实验内容和部分实验结果:
- 实验1一元线性预测kaggle房价
- 实验2多元线性预测kaggle房价,选择多种特征进行组合,完成多元线性回归,并对比不同的特征组合,它们训练出的模型在十折交叉验证上MAE与RMSE的差别,至少完成3组。
- 实验3对数几率回归完成垃圾邮件分类问题和Dota2结果预测,通过精度(accuracy),查准率(precision),查全率(recall),F1值对预测结果进行评估。
- 实验4线性判别分析完成垃圾邮件分类问题和Dota2结果预测,尝试对特征进行变换、筛选、组合后,训练模型并计算十折交叉验证后的四项指标:
由结果可以发现,线性回归模型中多元线性回归和对数线性回归精度类似并优于一元线性回归,对数线性回归精度优于线性判别分析。
实验中结果评价标准:
精度(accuracy),查准率(precision),查全率(recall),F1值,MAE,RMSE
标准说明:
(1).查准率(Precision),又叫准确率,缩写表示用P。查准率是针对我们预测结果而言的,它表示的是预测为正的样例中有多少是真正的正样例。
(2).精确度(Accuracy),缩写表示用A。精确度则是分类正确的样本数占样本总数的比例。Accuracy反应了分类器对整个样本的判定能力(即能将正的判定为正的,负的判定为负的)。
(3).查全率(Recall),又叫召回率,缩写表示用R。查全率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确。
(4).F1分数(F1 Score),是统计学中用来衡量二分类(或多任务二分类)模型精确度的一种指标。它同时兼顾了分类模型的准确率和召回率。F1分数可以看作是模型准确率和召回率的一种加权平均,它的最大值是1,最小值是0,值越大意味着模型越好。
(5).RMSE是均方根误差,它表示预测值和观测值之间差异(称为残差)的样本标准差。均方根误差为了说明样本的离散程度。做非线性拟合时,RMSE越小越好。
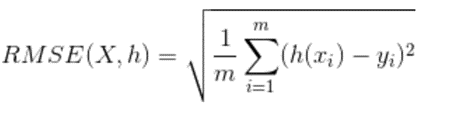
(6).MAE是是平均绝对值误差,它表示预测值和观测值之间绝对误差的平均值。是一种线性分数,所有个体差异在平均值上的权重都相等。

实验分析:
实验说明:
对十折交叉验证的理解:十折交叉验证就是将数据集分为十份,然后轮流使用其中的九份作为训练集,剩下的一份作为测试集。最终将10份预测值拼接后返回。利用这种方法,可以充分的使用数据集中的所有数据,从而在一定程度上可以减少过拟合的状况的发生。
2.决策树
实验内容和部分实验结果:
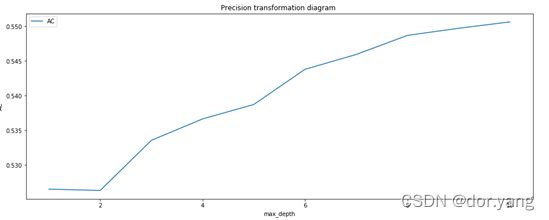
考虑到代码的运行时间(基本每种参数组合建树需要大概两三分钟),在代码中对于各个参数设置步长较大的list列表,通过不同参数建树后分析性能并输出最佳结果。

根据MAE图,我们选择最大深度为15,因为当最大深度小于15时,MAE快速下降,当最大深度大于10后,MAE基本不再变化,所以我们综合考虑模型精度和计算量的情况下选择最大深度为15
-
实验3使用信息增益,信息增益率,基尼指数完成决策树,并计算最大深度为6时决策时在训练集和测试集上的精度,查准率,查全率, F1值。

-
实验4实现使用信息增益率划分的预剪枝,计算出带有预剪枝和不带预剪枝的决策树的精度,查准率,查全率和 F1 值。
预剪枝的过程就是在每次选取一个最优的特征之后,根据所选择的划分标准,判断划分之后会不会比不划分的精度更高。只有在划分后精度更高的情况下才会继续往下递归,否则就把当前节点设为叶子节点并以当前节点样本数最多的类作为结果。
也就是说,实现预剪枝的过程,就是在创建决策树的过程中添加了一个预剪枝的判定条件作为递归程序的终止条件:如果当前结点划分后,模型的泛化能力没有提升,则不进行划分。

-
实验5实现带有后剪枝的决策树,在任意数据集中对比剪枝和不剪枝的差别。
实现后剪枝实际上首先要和实验三一样,构建一颗普通的决策树。然后对整个决策树自底向上的,考虑每一个节点直接作为叶子会不会有更好的精度,如果有更好的精度就将该节点直接变成叶子进行剪枝。

根据我们测试出的模型结果,我们可以看出有剪枝的模型在各个指标上均有提升,只是因为我们树的深度为6提升不是很明显
实验相关概念说明:
信息增益就是当前节点的信息熵和全部子节点信息熵综合的差。而全部子节点的信息熵的总和是对每一个子节点信息熵的加权平均。
其中:
![]()
IV(a)可以视为以子节点集合大小占当前节点集合大小的比例作为信息求了一个信息熵,并作为惩罚项,当子节点也分散,这个惩罚项的值就越大。
基尼指数用来衡量数据D的纯度,基尼指数的值越小表示数据的纯度越高。属性a的基尼值是以属性a划分,子节点基尼值根据集合大小的加权平均。
实验分析与总结:
“剪枝”是决策树学习算法对付“过拟合”的主要手段,预剪枝可通过“剪枝”来一定程度避免因决策分支过多,以致于把训练集自身的一些特点当做所有数据都具有的一般性质而导致的过拟合,同时显著减少训练时间和测试时间开销
但是预剪枝也会带来欠拟合风险,有些分支的当前划分虽然不能提升泛化性能,但在其基础上进行的后续划分却有可能导致性能显著提高。预剪枝基于“贪心”本质禁止这些分支展开,带来了欠拟合风险。
而后剪枝技术因为是在决训练策树完成后才进行自底向上的考察和剪枝,因此在获得更大的泛化性能的同时也付出了更大的开销时间的代价。
3.神经网络
实验内容和部分实验结果:
- 实验1使用 sklearn 自带的手写数字数据集完成手写数字分类任务,绘制学习率为 3,1,0.1,0.01 训练集损失函数的变化曲线
由图像可知,当参数learning_rate_init设置较大时,其训练效果会产生较大的起伏;而从整体来看,学习率越小,loss达到收敛时所需要的epoch就越多,即训练时间越长,以至于在learning_rate_init=0.01,max_iter = 250的参数设置条件下,loss没有达到收敛,因此其准确度相比于其他模型也要更低。
- 实验2使用梯度下降求解线性回归,了解标准化处理的效果
在按照提示完成代码开始运行之后,通过打印损失的信息我们可以看到损失值持续上升,这是因为我们的原始数据 X没有经过适当的处理,直接扔到了神经网络中进行训练,导致在计算梯度时,由于 X的数量级过大,导致梯度的数量级变大,在参数更新时使得参数的数量级不断上升,导致参数无法收敛。

对参数进行归一化处理,将其标准化,使均值为0,缩放到 [−1,1]附近后重新训练模型:

计算测试集上的MSE为:3636795867.3535
- 实验3完成对数几率回归,使用梯度下降求解模型参数,绘制模型损失值的变化曲线,调整学习率和迭代轮数,观察损失值曲线的变化,按照给定的学习率和迭代轮数,初始化新的参数,绘制新模型在训练集和测试集上损失值的变化曲线,完成表格内精度的填写


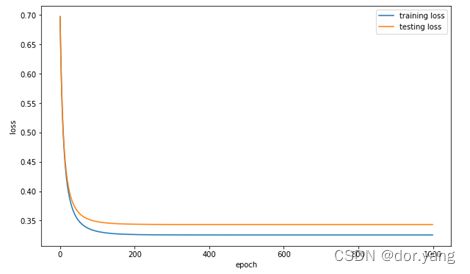
通过观察可以发现由于0.0001学习率太小,导致收敛速度过慢,loss的曲线甚至局部放大成了线性变化。而0.1的学习率就比较好,当训练到200轮左右的时候就已经开始收敛。因此在训练的时候如果选取了较大的学习率可以适当的将训练轮次减小,而当学习率较小的时候,需要适当的将训练轮次变大。
-
实验4实现一个三层感知机,对手写数字数据集进行分类,绘制损失值变化曲线,完成 kaggle MNIST手写数字分类任务,根据给定的超参数训练模型,完成表格的填写
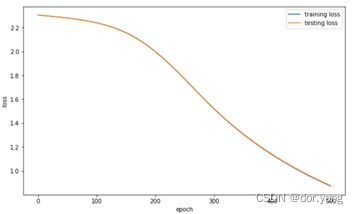
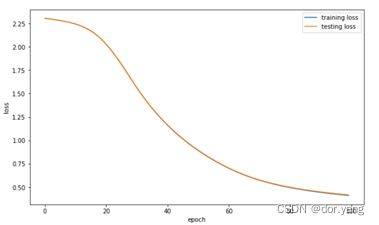
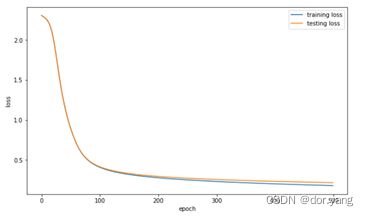
表中的前四行的数据仅在迭代轮数不同,因此通过观察学习率为0.1,迭代轮次为500的曲线图可以发现,模型在训练的过程中,loss从100轮次左右开始逐步收敛,在测试集和训练集的loss在200轮左右发生分离,也就是出现了一定的过拟合的情况。因此在表中的前四行数据中,可以看到随着迭代轮次的增加,精度是不断上升的。
而当学习率设为0.01后,因为更新的步长太小,所以可以发现尽管迭代轮次设为了500,训练的loss依然没有收敛,因此没有达到很好的精度。


实验分析与总结:
对比实验1不同的曲线可以看出,在训练的时候需要选取一个合适的学习率,学习率控制着算法迭代过程中的更新步长,如果学习率过大,则不容易收敛,如果过小,收敛速度容易过慢。
由实验3可以发现,当学习率较低时,模型准确率较低,并且损失值随着迭代轮数增加而线性减少。当学习率较高时,模型准确率较高,并且损失值会在很短的一段迭代轮数范围内迅速减少,后面随着迭代轮数增加减少不是很明显。比较二者,我们可知,在模型训练时,我们可以适当提高学习率,降低迭代轮数来实现高速高准确率的模型训练。同样的道理在实验4的实验过程中也有显示,因为学习率较低,导致收敛过慢,在500论迭代后依旧没有收敛,导致精度较低。