LCA-Tarjan算法

一开始从watashi的那本书中看了二分查找法跟RMQ法，也明白了思路，RMQ法是在线LCA算法，但我记得还有一种tarjan的离线算法。于是花了两个小时在网上查了一下，大致做了几道题。

下面以HDU2586为例简单说一下。

【题意】给定一棵树，每条边都有一定的权值(40000个点)，q次询问(500次)，每次询问某两点间的距离。

 

这道题基本上就是模板题了，网上随便一搜很多类似的题解。但很多都不是很详细。

 

首先明确几点，

1、  Tarjan算法是离线算法，需要预先读入所有的询问。

2、  Tarjan是基于并查集的。

3、  这个Tarjan算法跟求桥求连通块那个tarjan算法不一样（事实上tarjan发明过很多算法，貌似都叫tarjan算法）

 

这道题求路径长度，就是先求到根结点的距离dist[u]，询问点的最近公共祖先ans[u]

对于询问的u到v的路径，求出u，v的最近公共祖先x，然后答案就是dist[u]+dis[v]-2*dis[x]

 

这个是网上随便搜就能搜到的伪代码：

//parent为并查集，FIND为并查集的查找操作

//QUERY为询问结点对集合

//TREE为基图有根树

 Tarjan(u)

      visit[u] = true

      for each (u, v) in QUERY    //循环1

          if visit[v]

              ans(u, v) = FIND(v)

      for each (u, v) in TREE  //循环2，枚举与u相连的结点

          if !visit[v]

              Tarjan(v)

              parent[v] = u

 

基图有根树是什么我查了很久没查出来，最后翻了例题的代码发现，就是u为根结点的子树，第二个循环就是枚举与u相连的结点。

 

以watashi的书上的例子为例：

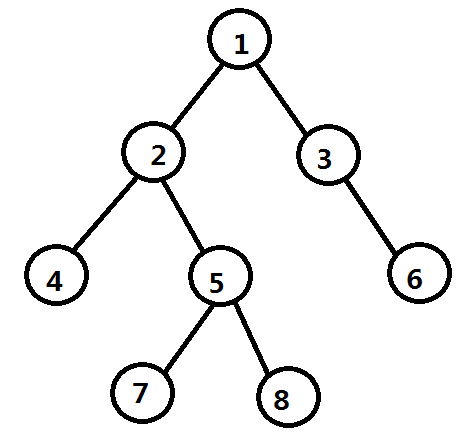
我们假设询问是(4,7),(6,8)

首先处理结点1，vis[1]设为true，因为其他都没有标记过，所以直接进入第二个for循环，处理它的子节点2和3

处理结点2，标记一下，然后找到询问(2,6)中有点2，但是6没有被标记过，所以跳过。接着枚举子节点。

处理结点4，跳过第一个循环，因为没有子节点，回溯到结点2，并将2与4合并到同一个并查集中（即4指向2）

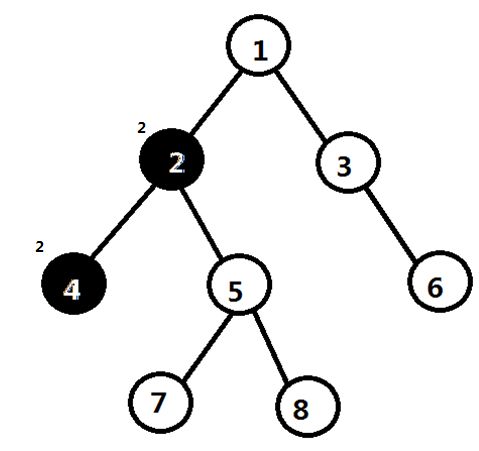
（左上角小数字的是结点在并查集中的根结点）

 

处理结点5，直接枚举其子节点

处理结点7，发现询问(4,7)中4之前标记过，所以输出并查集中的根结点2。(4,7的最近公共祖先是2)

处理结点8，回溯到5，将5,7,8均加入一个新的并查集中。

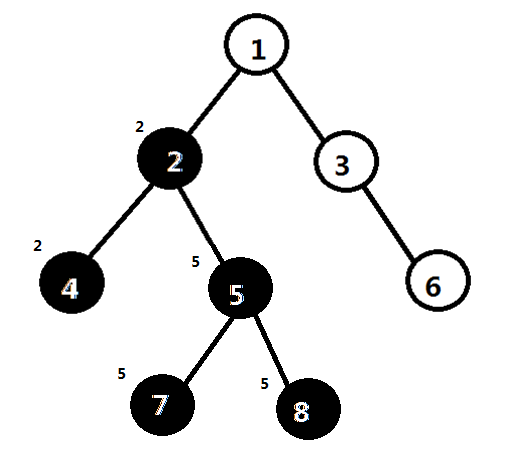
回溯到2时，再将2,4与5,7,8合并成一个新的并查集。

回溯到1时，在并查集中结点2指向结点1。

现在结点1的左子树已经全部处理完毕了。

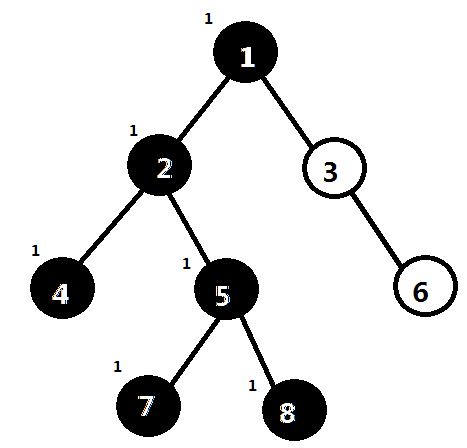
接下来DFS到6时，注意到结点8已经标记过了，直接找到结点8在并查集中的根结点（结点1），即6跟8的最近公共祖先。

 

为什么呢，如果对于结点X，我们已经扫描完了左子树，那么它的左子树连同结点X一定在同一个并查集中，且根为结点X，如果存在询问(u,v)，其中u在左子树中，v在右子树中，当DFS到v结点时，显然u所在并查集的根X是它们的最近公共祖先。

 

具体到这道题，我们用dist[i]表示结点i到根结点的距离，在DFS中就可以计算出来：dist[v]=dist[u]+w其中w为(u,v)的权值。

 

然后对于每个询问u,v，找到最近公共祖先x，计算dist[u]+dis[v]-2*dis[x]即可。

 

代码：

/*From http://cnblogs.com/zhyfzy */ 

#include<cstdio>

#include<cstring>

#include<cmath>

#include<iostream>

#include<algorithm>

#include<set>

#include<map>

#include<stack>

#include<vector>

#include<queue>

#include<string>

#include<sstream>

#define eps 1e-9

#define ALL(x) x.begin(),x.end()

#define INS(x) inserter(x,x.begin())

#define FOR(i,j,k) for(int i=j;i<=k;i++)

#define MAXN 40005

#define MAXM 80005

#define INF 0x3fffffff

using namespace std;

typedef long long LL;

int i,j,k,n,m,x,y,T,ans,big,cas,num,len;

bool flag;

int u,v,w,d;

int edge,head[MAXN];



int fa[MAXN],query[MAXN][3],dist[MAXN];

bool vis[MAXN];



struct node

{

    int v,id;

    node (int _v,int _id):v(_v),id(_id){}

};



int find(int x)

{

    if (x==fa[x]) return fa[x];

    return fa[x]=find(fa[x]);

}



vector <vector<node> > mp;



struct edgenode

{

    int to,next,w;

} G[MAXM];



void add_edge(int x,int y,int w)

{

    G[edge].to=y;

    G[edge].w=w;

    G[edge].next=head[x];

    head[x]=edge++;

}





void tarjan(int u)

{

    vis[u]=true;

    for (int i=0;i<mp[u].size();i++)

    {

        int v=mp[u][i].v,id=mp[u][i].id;

        if (vis[v]) query[id][2]=find(v);

    }

    

    for (int i=head[u];i!=-1;i=G[i].next)

    {

        int v=G[i].to,w=G[i].w;

        if (!vis[v])

        {

            dist[v]=dist[u]+w;

            tarjan(v);

            fa[v]=u;

        }

    }

}





int main()

{

    scanf("%d",&T);

    while (T--)

    {    

        memset(head,-1,sizeof(head));

        edge=0;

        

        scanf("%d%d",&n,&m);

        for (i=0;i<n-1;i++)

        {

            scanf("%d%d%d",&u,&v,&w);

            add_edge(u,v,w);

            add_edge(v,u,w);

        }

        

        mp.clear();

        mp.resize(n+4); 

        

        for (i=0;i<m;i++)

        {

            scanf("%d%d",&u,&v);

            query[i][0]=u;

            query[i][1]=v;

            mp[u].push_back(node(v,i));

            mp[v].push_back(node(u,i));

        }

        for (i=1;i<=n;i++) fa[i]=i;

        memset(vis,0,sizeof(vis));

        dist[1]=0;

        tarjan(1);

        

        for (i=0;i<m;i++)

        {

            u=query[i][0];

            v=query[i][1];

            d=query[i][2];

            printf("%d\n",dist[u]+dist[v]-2*dist[d]);

        }

    }

    return 0;

}