MySql进阶索引篇01——深度讲解索引的数据结构:B+树
深度讲解索引的数据结构:B+树
-
-
-
- 1.索引介绍
-
- 1.1 为什么使用索引
- 1.2 索引的优缺点
- 2.从零开始设计索引
-
- 2.1没有索引时怎么查询数据
- 2.2 基于页的目录项的简单索引
- 2.3 InnoDB索引设计方案
-
- 2.3.1 迭代1:目录项的数据页(目录页)
- 2.3.2 迭代2:多个目录页
- 2.3.3 迭代3:目录页的目录页
- 3.索引类型
-
- 3.1.聚簇索引
- 3.2 二级索引
- 3.3 联合索引
- 3.4.InnoDB的B+树注意事项
-
- 3.4.1 根页面位置万年不动
- 3.4.2 内节点中目录项记录具有唯一性
- 3.4.3 一个页面最少要存储两条记录
- 4.MyISam的索引方案
-
- 4.1 不同存储引擎索引的区别
- 4.2 MyISam索引的原理
- 4.3 MyISam与InnoDB索引方案的对比
- 4.4 索引方案与索引优化的关系
- 5.索引的代价
- 6.B+树与常见的查找数据结构对比
-
- 6.1 Hash结构
- 6.2 二叉搜索树
- 6.3 AVL树
- 6.4 B树
- 6.6 B+树
- 6.7 R树
-
-
1.索引介绍
1.1 为什么使用索引
索引是存储引擎中一种用于快速找到数据的存储结构,他就像《新华字典》的目录,可以使我们查每个字的速度大大提升。
下面将
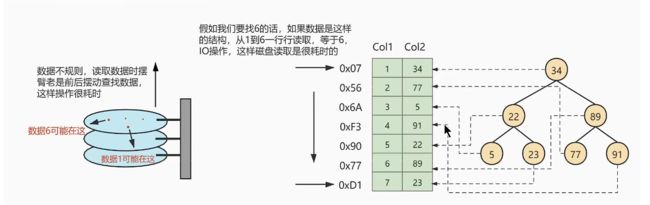
结合计算机的存储带大家深入理解索引的优点。下图左边使一个磁盘,在这个磁盘中存放数据是随机的,如果要查找某条数据,需要在整个磁盘空间进行扫描,十分耗时。下图右边(表格部分)改进了这一做法,在磁盘中开辟了一块连续的存储空间,数据也是连续存储,如果我们需要找第六条数据,只需要进行顺序访问,时间复杂度是O(n).
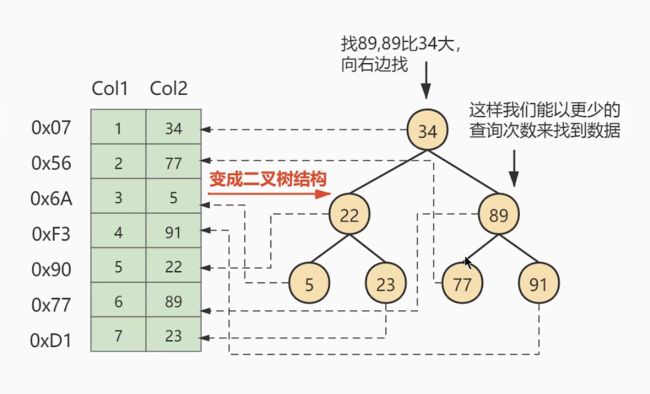
还可以改进吗?当然可以,结合我们熟悉的二分查找算法,我们可以使用二叉搜索树来优化。如下图,只要构造一颗二叉树,让左子树的值比右子树的小即可。同样是要查找之前的第六条数据,也就是89,只需要查找2次就可以了。其时间复杂度为 O ( l o g 2 n ) O(log_2n) O(log2n)
实际上,MySQL数据库的索引就是建立了一棵B+树(其它存储引擎不一定),比上面的二叉搜索树更加复杂一点。左图转为右图就与索引的创建过程类似,它的创建有利于减少查找数据时的磁盘I/O次数,提高查找速度。注意,这里提到的磁盘I/O其实是很耗时的。因此它的减少会大大提升我们的时间性能。
1.2 索引的优缺点
(1)优点
- 减少磁盘I/O,提升数据查找速度(主要原因)
- 创建数据的唯一约束,会自动创建该数据的唯一索引,保证数据库中每一行数据的唯一性
- 对有依赖关系的子表与父表进行联合查找时,可以加快表与表连接(通过主键关联),提升查找速度(后面将讲解)
- 在建立分组(group by)与排序(order by)时,可以减少减少查询中分组与排序的时间,降低cpu的消耗
(2)缺点
- 创建与维护索引需要时间,并且随着索引中数据字段的增减,所耗费时间也会增加
- 索引需要占用磁盘空间进行存储
- 降低了更新数据表的速度(增、删、改都需要动态的维护索引)
注:在实际的生产中,如果需要批量的删除、增加、修改数据,可以先把索引删除,完成操作后再重新的建立索引。
2.从零开始设计索引
从Mysql5.5之后使用的存储引擎默认为InnoDB,因此我们以InnoDB为例,从0开始设计、迭代索引。
2.1没有索引时怎么查询数据
如果查询一条数据,我们可以使用如下查询语句:
select [列名] from [表名] where [过滤条件]
(1)在同一个页进行查询
如果数据量不是很多,可以在一个页存储完(16kb),查询有两种情况:
-
按照主键查找,因为主键是有序的,可以使用二分法查找,时间复杂度为 O ( l o g 2 n ) O(log_2n) O(log2n)
-
按照其它列查找,需要遍历单链表(数据库的元素实际上是单链表形式实现逻辑上连续的),时间复杂度为O(n)
(2)在多个页存储
如果数据多到一个页存储不下了,需要在多个页中进行查询,需要
- 定位到数据所在的页
- 从所在的页中查找记录
因为数据页之间数据没有关联(并不是数据页2的数据的主键就比数据1中存储的数据主键大,数据页之间是相对对立的),因此需要遍历数据页,然后在每个数据页再对数据进行查找。除了遍历数据页外,我们还需要把这些数据页从物理磁盘加载到内存中,这个过程也是十分消耗时间的。成百上千的页加载、遍历消耗的时间无法忍受,于是索引运势而生。
2.2 基于页的目录项的简单索引
建立一张表
CREATE TABLE index_demo(
c1 INT,
c2 INT,
c3 CHAR(1),
PRIMARY KEY(c1)
) ROW_FORMAT= Compact;
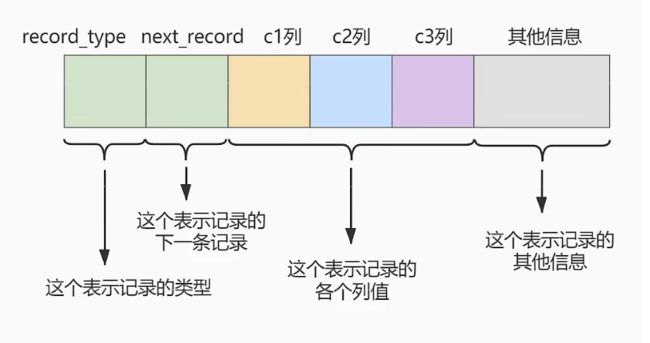
compact是一种记录的存储格式,后面将详细介绍,这里简单介绍如下。
其中record_type表示 记录类型,0表示普通记录,2表示最小记录,3表示最大记录,1暂未使用。
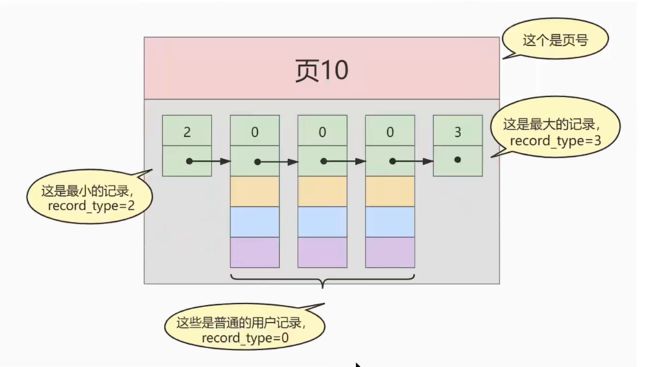
一个基本的数据页模型就长这样。
假设每页可以存储三条记录(实际上远远不止)。在表中插入三条记录。
INSERT INTO index_demo VALUES (1,4,'u'),(3,9,'d'),(5,3,'y');
这样他们就串联成为如下图所示的单链表了。
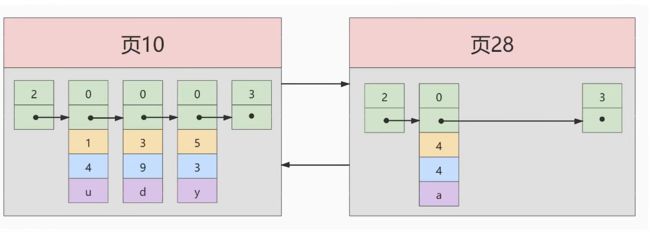
此时我们再插入一条记录。
INSERT INTO index_demo VALUES (4,4,'a');
由于一个页只能存放三条数据,我们必须分配一个新的页(页28的28是随便写的,实际上应该是页地址)。
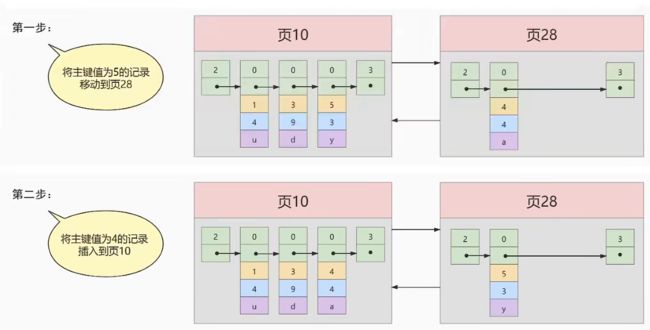
上图是不是合理的呢?似乎主键值为不是顺序递增了,我们下面将给主键建立索引。先把主键为5的记录与主键为4的记录交换下位置,这个过程称为记录移动。
在数据记录进行增删改时,我们必须通过记录移动保证记录的主键值始终保持递增排列,这个过程我们称之为页分裂。
在插入许多数据以后,数据存储可能是这样的。
由于数据页的编号并不是连续的,我们如果需要查询一个数据,我们需要依次在各个数据页中进行查找,这样老费劲了。因此,我们可以考虑开辟一个连续存储空间,用于存放一个给所有数据页建立的目录项。如下图,目录项中key为页的首个记录主键值,page_no为页号。
比如我们需要查找一个主键值为20的记录,目录项1的key为1,目录项的key为2,由此可知目录项1所在的page10肯定没有我们的目标记录。同样的道理,目录项2的页28,目录项4的page20都没有我们的记录,我们只需要在目录项3所在的page9使用二分法去查找就可以了。实际上,在对于目录项过滤时同样页可以用二分法,而不用逐个目录项进行比较、判断。
2.3 InnoDB索引设计方案
下面对于2.2中所提到的索引设计方案进行迭代,一步步解密InnoDB索引设计方案。
2.3.1 迭代1:目录项的数据页(目录页)
上面提到,如果目录项在存储空间是顺序存储的,我们可以可以使用二分法来判断目录项是否有我们需要查询的数据。实际上,这个方案存在许多问题,我们不妨思考以下几个问题。
- 如果目录项的数量特别多,我们还可以在物理存储空间中为它开辟这么一大块连续的存储空间来存储目录项吗?
- 如果需要删除中间某一个目录项的数据,其它目录项的位置都需要依次向前移动。
- 如果我们在中间插入了3个主键连续数据(与之前假定的每页记录数一样),相当于在目录项中间新增了一个目录项,后面的目录项都需要移动位置。
我们于是考虑,不能使用顺序存储的方式来存储目录项,而应该使用单项链表形式来存储目录项,使他们在逻辑上连续。
因此我们就可以把目录项也放到一个数据页中,其record_type中为1,如下图所示。
目录项的数据页与普通数据页都会建立一个页目录,这样在查找记录时就可以使用二分法加快查询速度,这也解决了链表不能够二分查找的问题,后面我们将详细的介绍页目录的知识。
2.3.2 迭代2:多个目录页
试想下,如果数据页的数量较多,一个目录页不够用了,那怎么办呢?我们其实可以如法炮制:增加目录页。
这时候如果我们需要查询一个数据,就首先需要判断数据是在页30中还是在页32中了。是不是熟悉的配方,熟悉的味道。
2.3.3 迭代3:目录页的目录页
为了解决多个目录页需要遍历查找的问题,我们可以再套一层娃:给目录页增加一个目录页。
![]()
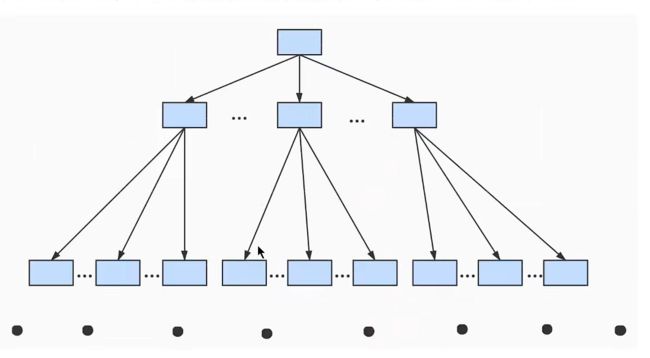
随着表中记录数的增加,层数可能还会增加。我们将上图简化如下。这其实就是传说中的B+树了。
实际上,一般实际开发中,B+树几乎不会出现超过四层的情况,因为我们知道,一个数据页有16KB,即使假设每个记录需要160字节,一个数据页页可以存放100条数据,而目录页需要存放的数据大小更小,假设一个目录页可以存放1000个数据。那么四层B+数可以存放的记录数就是:100 * 1000 * 1000 * 1000 = 1000,0000,0000 。1000亿条记录!!!这就意味着,我们查找一次数据,最多需要4次磁盘I/O操作(加载4个数据页)。
3.索引类型
3.1.聚簇索引
聚簇索引:基于主键构建的索引称之为聚簇索引。非聚簇索引:基于非主键构建的索引称之为非聚簇索引。
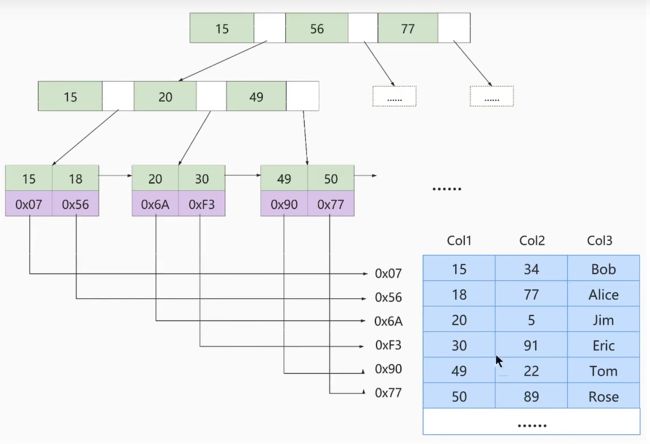
实际上,聚簇索引并不是一种单独的索引类型,而是一种数据的底层存储方式,它的叶子节点会存储完整的数据记录。数据即索引,索引即数据。前面我们创建的实际上就是聚簇索引(如下图)。而非聚簇索引的叶子节点中并不会存储我们完整的数据记录。
![]()
聚簇索引并不需要我们显示的用index去创建,mysql的InnoDB引擎会自动的帮我们创建聚簇索引。
它的优点有:
- 查询速度更快。聚簇索引把索引和数据保存在同一个B+树中,相比非聚簇索引查询速度更快。
- 聚簇索引对于主键的排序查找和范围查找很快。
- 降低了磁盘I/O操作的次数,提升了查找效率(索引的优点)
缺点有:
- 插入性能依赖于插入顺序,如果我们按照主键进行升序插入,那么插入数据的效率肯定是最高的,否则可能会出现页分裂,严重影响性能。因此,对于InnoDB引擎,我们一般会定义一个自增的列为主键。
- 更新主键的代价很高。更新主键将导致被更新的行移动,我们一般定义,在InnoDB引擎中,主键不可更新。
- 二级索引(后面介绍)要经过两次索引查找,一次找到主键值,第二次根据主键值找到行数据。
聚簇索引有以下几点需要注意:
- 对于Mysql数据库,MyISAM搜索引擎一般没有聚簇索引,InnoDB支持聚簇索引。
- 由于数据的物理存储方式只能有一种,一个表只能有一个聚簇索引,一般就是使用主键;如果没有指定主键,InnoDB会自动选择一个非空唯一索引构建聚簇索引;如果没有合适的字段,InnoDB会隐式的创建主键构建聚簇索引。
3.2 二级索引
二级索引又称为非聚簇索引,辅助索引。一个表中只允许有一个聚簇索引,但是允许有多个二级索引。如果我们需要依赖非主键进行查找,就需要二级索引了。
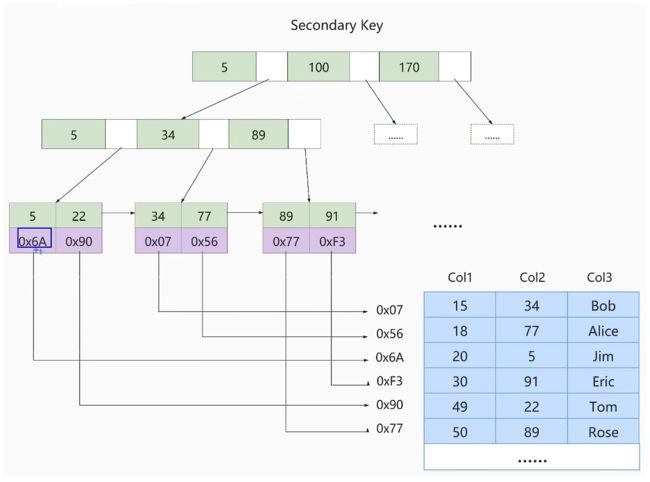
如下图,二级索引的叶子节点并不会存储完整的数据,只是存储了建立索引的列的值与主键值。
我们如果需要进行如下查找:
select * form index_demo where c2 = 4
需要先在二级索引中查找到对应的数据项,也就是主键为1,4,10的记录,再到聚簇索引中去查找对应主键值的数据,这个过程我们称之为回表。
对于聚簇索引,数据的查询效率更高(不用回表)。但是对于非聚簇索引,更新数据的效率更高,比如我们更新一个记录的c3列的值,对应的聚簇索引的值也需要进行更新,但是c2的二级索引并没有存储c3的数据,因此不用更新。
3.3 联合索引
严格来说,联合索引属于非聚簇索引。设想如下场景。
(1)对于数据基于c2排序
(2)如果c2数据相同则基于c3排序
这种场景就可以建立联合索引。
3.4.InnoDB的B+树注意事项
3.4.1 根页面位置万年不动
前面我们在介绍时,为了方便大家的理解,先把叶子节点构建了出来,然后往上增加层次。实际上,B+树的形成过程是这样的。
- 当我们创建一个新的索引时(或者主键自动生成新的索引时),初始时将会创建一个节点作为根节点,此时根节点中没有用户记录,也没有数据项记录。
- 当插入记录时,记录会被插入到根节点。
- 当根节点的记录满了,会分配一个新的数据页,比如数据页A,将根节点的数据全部拷贝到数据页A中,然后数据页进行页分裂操作得到页B,此时插入数据时再根据键值大小(主键值大小或者索引列值大小)决定插入到数据页B中还是数据页A中。
- 根节点会晋升为目录页。
根节点万年不动的原则保证InnoDB数据需要使用某个索引时可以在固定位置取出根节点的页号,从而来访问这个索引。
3.4.2 内节点中目录项记录具有唯一性
我们知道B+树的目录页中存储的记录为页号+索引列数据,这样的描述其实并不严谨。
假设index_demo表中的数据如下表。
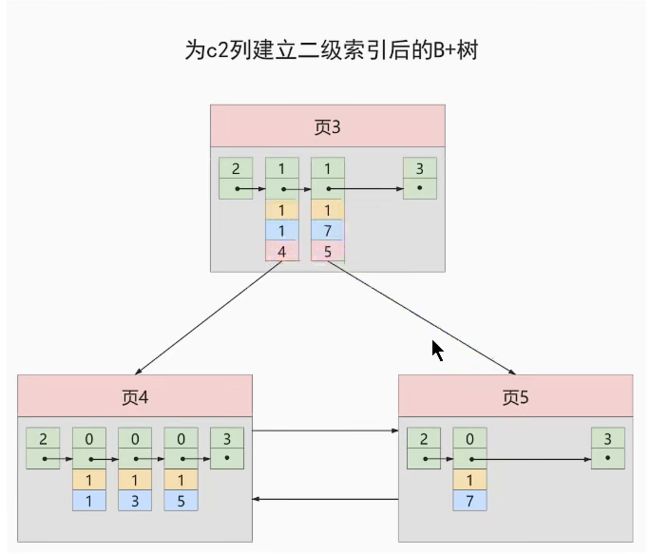
此时建立的二级索引B+树如下图。
如果我们需要增加一个记录(9,1,‘c’),我们是应该把这个记录添加到页4还是页5呢?
因此我们必须要求内节点(非叶子节点)的记录(除页号)是唯一的。如何能够实现呢?我们可以自然联想到主键是唯一的。因此下图才是我们实际上真正构建的二级索引的B+树。
此时添加记录(9,1,‘c’)就不迷惑了。我们先判断c2一样,再判断主键值,可以确定应该在页5中添加数据。
3.4.3 一个页面最少要存储两条记录
如果一个页面的记录数少于两条,甚至都无法分为二叉树,只是简单的单向连接。
4.MyISam的索引方案
4.1 不同存储引擎索引的区别
B+树适用的存储引擎如下所示。
注:MySql官方中写的B-Tree就是我们所理解的B+树。
InnoDBheMyISAM默认索引都是B-Tree,不过MyISAM中叶子节点data域中存放的是数据记录的地址。而Memory支持的默认索引是Hash索引。
4.2 MyISam索引的原理
下面我们将介绍MyISam的索引原理。MyISam使用myd文件存储数据,用myi文件存储索引,MyISam的存储原理与InnoDB的聚簇索引的存储原理显然不同(索引即数据,数据即索引)。实际上,MyISam中根本不存在聚集索引的概念,它的索引都相当于二级索引。
其索引存储示例如下。
上图的col1是主键,一般我们都是按照主键递增来增加数据的 ,但如果我们增加一条主键为3的数据,还需要进行重新排序吗?答案是否,它会被直接添加到表格后,不进行排序。
实际上如果针对col2建立索引,与基于主键构建索引在结构上并没有什么不同。
4.3 MyISam与InnoDB索引方案的对比
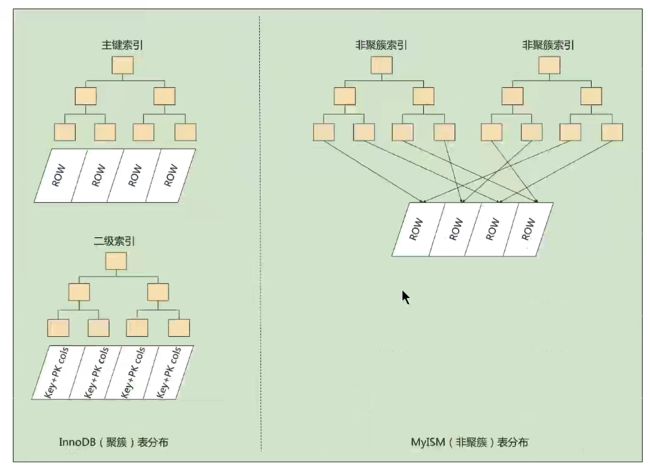
- MyISam的索引不存储记录的数据值(或主键值),只存储数据地址,一定需要进行回表操作。
- InnoDB的数据文件与索引文件是同一个,MyISam的数据文件与索引文件是分离的。
- MyISam回表操作十分快速,因为是拿着地址的偏移量直接到文件中取数据。
- InnoDB必须要有主键(如果没有会隐式指定),MyISam没有聚簇索引与二级索引的说法,不需要在二级索引中查找到主键值后再去聚簇索引中查询回表,因此并不是必须需要有主键。当然,我们为了查询方便,也会对该存储引擎的表设置索引。
4.4 索引方案与索引优化的关系
了解不同存储引擎的存储方案有利于我们进行索引优化。
例1:
InnoDB搜索引擎的主键值就不宜设置的过长,因为在所有二级索引中都需要对主键值进行存储。
例2:
用非单调(递增、减)字段在InnoDB存储引擎的表中做主键不合适。因为InnoDB的数据文件本身就是一棵B+树,会基于主键建立聚簇索引。导致我们在插入数据时频繁的发生页分裂。
5.索引的代价
索引的代价主要是空间与时间代价。
- 空间上:创建索引需要存储空间。一个数据页的存储空间是16kb,如果一棵B+树有很多数据页,将会消耗较大的存储空间。
- 时间上:进行数据的增删改操作,同时需要对索引进行维护。主要是页面移动、页面回收、页分裂等代价。
后面的博客中,我们也将一起学习在哪些字段上适合创建索引。
6.B+树与常见的查找数据结构对比
Mysql索引的作用就是减少I/O次数,从而实现数据查找速度的提升。因此我们将以这个作为目标深入对比Hash索引,ALV树,B树和B+树,从而剖析为什么要选择B+树作为Mysql的索引底层数据结构。
6.1 Hash结构
一般提到要加快查找的速度,我们都会考虑两种数据结构:树和哈希。哈希算法的查找效率很高,可以很快的定位到数据的具体位置,通常1次检索,时间复杂度平均为 O ( l o g 2 n ) O(log_2n) O(log2n)
而B+树还需要多次I/O,时间复杂度为 O ( n ) O(n) O(n)
HashMap就是典型的Hash算法应用实例,下图展示了HashMap的数据结构。
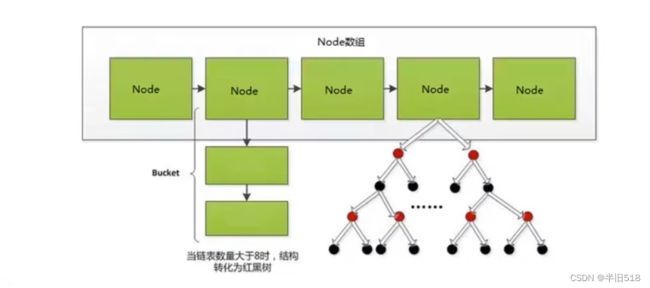 哈希算法可以通过计算使一个
哈希算法可以通过计算使一个key对应唯一value。这样我们就可以通过哈希算法计算数据应该存储的地址,把一个数据映射到一个地址。
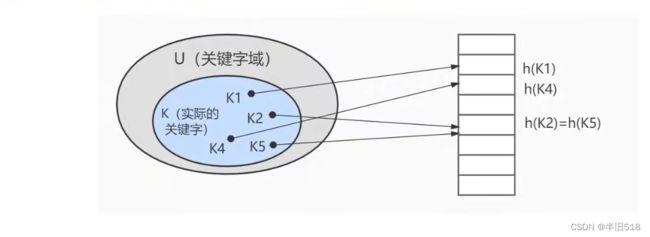 但有时候,可能会出现两个
但有时候,可能会出现两个key计算得到的地址相同的情况,我们称之为碰撞。这时我们
可以通过链接法解决。
 如下Demo01是采用普通算法进行搜索,输出时间是
如下Demo01是采用普通算法进行搜索,输出时间是1604ms.
public class Demo01 {
public static void main(String[] args) {
int [] arr = new int [100000];
for (int i = 0; i < 100000; i++) {
arr[i] = i ;
}
long start = System.currentTimeMillis();
for (int i = 0; i < 100000; i++) { // search 10000 times
int temp = i;
for (int j = 0; j < arr.length; j++) {
if(temp == arr[j]) {
break;
}
}
}
long end = System.currentTimeMillis();
System.out.println("cost " +(end - start) + " ms.");
}
}
下面算法则花费时间9ms,显然hash算法的查找效率比全表扫描快很多。
public class Demo02 {
public static void main(String[] args) {
HashSet set = new HashSet(100000);
int [] arr = new int [100000];
for (int i = 0; i < 100000; i++) {
set.add(i);
}
long start = System.currentTimeMillis();
for (int i = 0; i < 100000; i++) { // search 10000 times
int temp = i;
set.contains(temp);
}
long end = System.currentTimeMillis();
System.out.println("cost " +(end - start) + " ms.");
}
}
既然hash算法的查询效率这么高,为什么InnoDB、MyISam的索引结构要设计成为树型解构呢?
- hash算法主要适用于等值判断(==,In查询),对于范围查询,还是只能通过全表扫描来完成,时间复杂度将会退化为
O(n). - Hash算法存储元素是无序的,如果需要进行
OrderBy等操作无法完成。 - Hash算法不适合进行联合索引的查询。
- 当索引列重复元素较多时(比如性别),会造成大量的哈希冲突,解决哈希冲突将导致效率较低,查找效率也会变低。
总结来说,索引操作并不是只进行等值判断,或者重复元素较多的列,不适合使用hash索引。
索引引擎对于hash索引的支持情况如下图。
 hash结构的索引适用于
hash结构的索引适用于key-value型的数据库,Redis是现在很火的非关系型数据库,它的底层核心就是hash索引。Mysql中如果需要频繁的对索引进行等值判断,可以考虑使用Memory引擎。
另外,InnoDB虽然不支持Hash结构的索引,但是它提供了自适应哈希索引(Adapter Hash Index).如果某个数据页经常被访问,其地址就会被存储到哈希表中,这样下次访问时就可以直接找到这个页面的位置,这也使B+树具备了hash索引的优点。其过程可以参考下图理解。
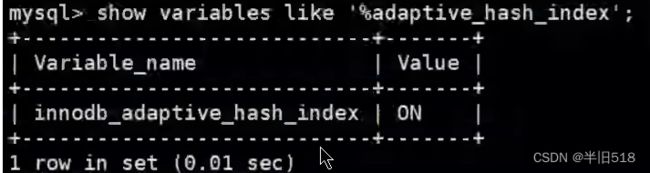
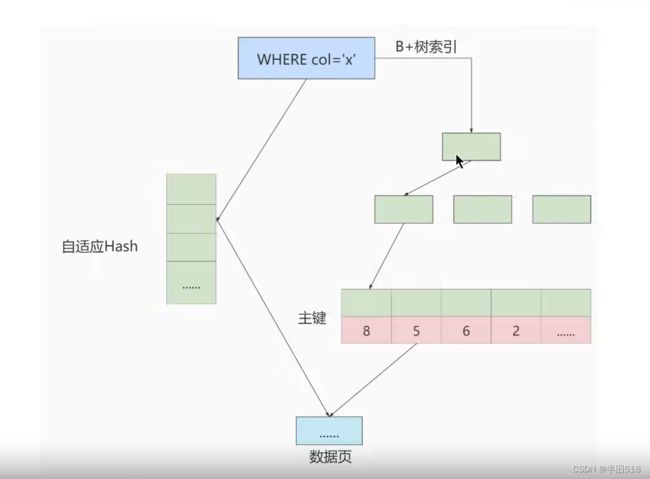 可以通过如下命令查看数据库中是否开启了自适应hash索引。
可以通过如下命令查看数据库中是否开启了自适应hash索引。
6.2 二叉搜索树
二叉搜索树具有如下特点:
- 一个节点最多有两个子节点,也就是节点的度不能超过2
- 每个节点左子结点<本节点<右子节点。
其结构可以参考下图。
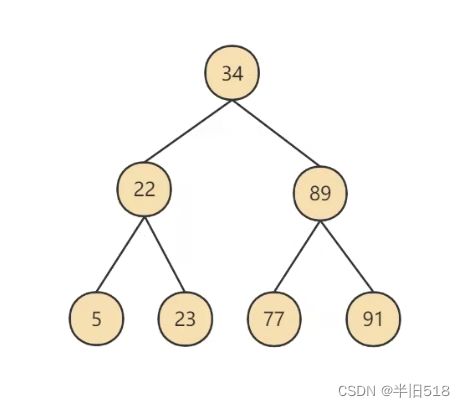
二叉搜索树的查找很简单,从根节点开始查找,如果查找元素比当前节点小,则在左子树中查找,如果查找元素比当前节点大,则去右子树中找。如果相等,则返回当前节点。二分查找就是利用二叉搜索树实现的。其平均时间复杂度也是 O ( l o g 2 n ) O(log_2n) O(log2n)
但是二叉搜索树的最大时间复杂度也是 O ( n ) O(n) O(n)
因为当数据是有序时,构建的二叉搜索树会退化为线型结构哦。
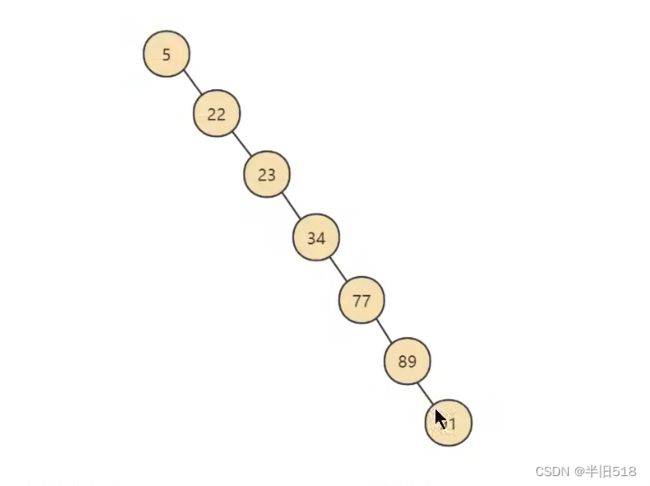 为了避免出现上面的情况,我们需要对二叉搜索树的深度进行限制,AVL树就做到了这一点。
为了避免出现上面的情况,我们需要对二叉搜索树的深度进行限制,AVL树就做到了这一点。
6.3 AVL树
AVL树即平衡二叉搜索树。AVL树可以是空树,除了这种特殊情况外,它要求:
- 左、右子树的高度差不能超过1
- 左、右子树也都是一棵平衡二叉树
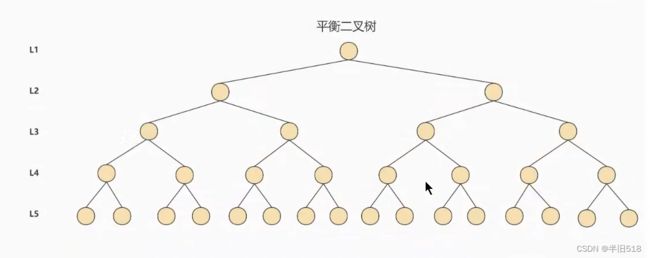 上面的平衡二叉树查找一个元素最多需要五次I/O操作,有没有办法让其查找效率更高呢?
上面的平衡二叉树查找一个元素最多需要五次I/O操作,有没有办法让其查找效率更高呢?
我们可以把二叉树变成m叉树,比如同样多数量的节点,在下图的三叉树中只需要四次I/O操作就可以查找到一个元素了。
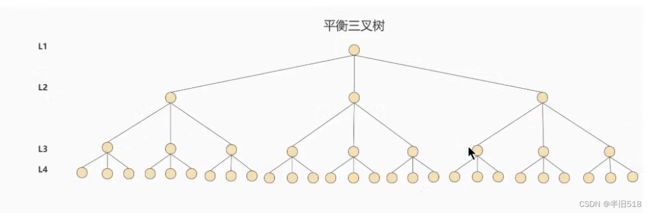 基于这种把树变矮胖,从而减少树的层数的思想,我们设计了B树。
基于这种把树变矮胖,从而减少树的层数的思想,我们设计了B树。
6.4 B树
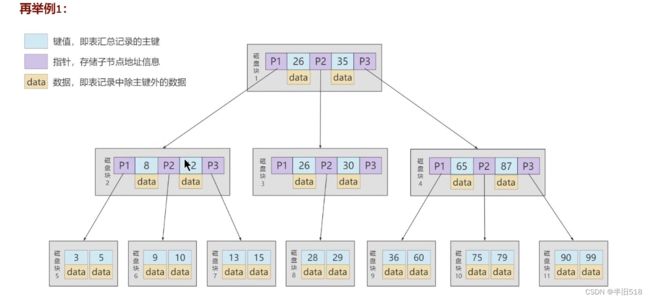
B树的英文是Blance Tree,又称为多路平衡查找树。B树的结构如下图。
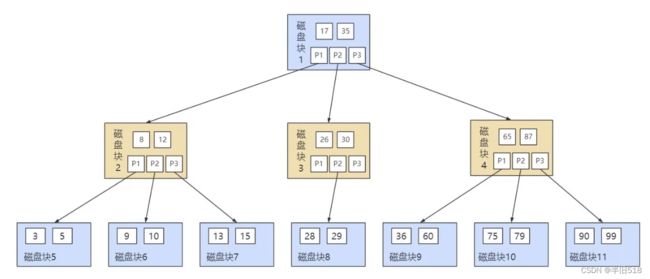
我们可以观察下它的特点。上面磁盘块1中有两个元素,分别是17和35,磁盘块2的元素都小于17,磁盘块3的元素位于17与35之间,磁盘块4的元素都大于35.
在一棵B树中,子结点数量的最大值称为阶,上图中B树的阶为3.
我们不妨回顾下B+树,然后看看B树与B+树有何不同。
![]() 我们看到,页30的节点中存储了index和page_no,而它的子结点页10则存储了具体的记录数据。但B树的叶子节点与非叶子节点存储的信息都完全独立。换句话说,B树的节点不存在上下级关系。如果使用B树作为索引的数据结构,我们需要在每个节点中存储完整的记录信息。
我们看到,页30的节点中存储了index和page_no,而它的子结点页10则存储了具体的记录数据。但B树的叶子节点与非叶子节点存储的信息都完全独立。换句话说,B树的节点不存在上下级关系。如果使用B树作为索引的数据结构,我们需要在每个节点中存储完整的记录信息。
B树具有如下特性。
- 如果插入数据、删除数据导致树不平衡,会自动调整至平衡。
- 关键字集合在整个树中,即叶子节点与非叶子节点都存放数据,搜索可能在叶子节点中结束。
6.6 B+树
B+树其实是在B树的基础上进行的改进。B+树更加适合文件索引的系统。现在总结下B树与B+树的区别。
![]()
- 在B+树中,一个节点有k个孩子(子结点)就有k个关键字(data),而在B树中,一个节点的孩子树=关键字数+1。
- B+树非叶子节点只用于索引,不存储数据.而B树中各个节点存储的都独立存储数据。
- B+树所有关键字都在叶子节点出现,并且叶子节点之间通过双向链表来彼此链接,叶子节点内的数据按照顺序使用单链表连接。
上面我们提到了B+树的中间节点只用于索引,不存储数据,这有什么好处呢?
- B+树的查询效率更加稳定。每次查找的
I/O次数更少。 - B+树的查询时I/O次数更少,查询效率更快。因为B+树的非叶子节点只用于索引,不存储数据的信息,就可以有更多的子树,这会使其更加矮胖,也就是阶数更低,查询时I/O次数更少。
- B+树的范围查询效率更高,由于B+树的叶子节点存储了所有的记录信息,并且是按照顺序排列,我们在查找时通过链表指针就可以快速进行范围查询了。
6.7 R树
另外对于地图等高维搜索空间问题一般使用R树作为索引的数据结构,MySQL不支持使用R树作为索引。