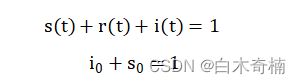数学建模基于传染病SIR模型MATLAB源码
初始条件:
(2)
我们可以得到人数变化机制,也即:
健康人群的下降率:-λNs(t)i(t);
患病个体的增长率:λNs(t)i(t)-Ni(t);
解除患病个体的增长率:Ni(t);
由此,我们可以建立模型:
对两边化简,并对t求导可得:
此式的微分方程组即为高校模型核心方程。
1. clc
2. clear
3. close all;
4. A = 0.4;%密接的健康者数目与此环境内健康者总数成正比
5. B = 1/14;%移出的人数与正在患病数量成正比
6. I = 0.04;%患病人比例
7. S = 1-I;%健康人比例
1. %ode
2. tspan = [0 100];
3. y0 = [I S];
4. [t, y] = ode45(@(t,y)odefun(t,y,A,B), tspan, y0);
5. r = 1-y(:,1)-y(:,2);
1. %euler
2. n = size(r,1);
3. h = 50 / (n-1);
4. t_0 = [0:h:50]';
5. y_i = zeros(n,1);
6. y_s = zeros(n,1);
7. y_i(1) = I;
8. y_s(1) = S;
9. for i = 1:n-1
10. y_i(i+1) = h*[A*y_i(i)*y_s(i) - B*y_i(i)]+y_i(i);
11. y_s(i+1) = h*[-A*y_i(i)*y_s(i)]+y_s(i);
12. end
13. r_0 = 1 - y_i(:,1) - y_s(:,1);
1. %画图
2. subplot(2,2,1);
3. plot(t,y(:,1),'-o',t,y(:,2),'-.',t,r,'g');
5. hold on;
6. legend('患病人数:i(t)','健康人数:s(t)','移除人数:r(t)','Location','Best');
7. ylabel('占人口比例%');
8. xlabel('时间t');
9. str = ['接触健康者概率λ/μ:',num2str(A/B),' 初始患病人数:',num2str(I),',初始健康人10数:',num2str(S)];
10. text(15,0.4,str,'FontSize',10);
11. title('SIR模型(ode)');
1. subplot(2,2,2);
2. plot(t_0,y_i,'-o',t_0,y_s,'-.',t_0,r_0,'g');
3. hold on;
4. legend('患病人数:i(t)','健康人数:s(t)','移除人数:r(t)','Location','Best');
5. ylabel('占人口比例%');
6. xlabel('时间t');
7. str = ['接触数λ/μ:',num2str(A/B),' 初始患病人数:',num2str(I),',初始健康人数:',num2str(S)];
8. text(15,0.4,str,'FontSize',10);
9. title('SIR模型(euler)');
1. subplot(2,2,3);
2. plot(t_0,y_i,'r-',t,y(:,1),'-.');
3. diff = sum(abs(y_i - y(:,1)));
4. str1 = ['患病人数对比图i(t), 误差:',num2str(diff)];
5. title(str1);
6. legend('euler','ode','Location','Best');
7. ylabel('占人口比例%');
8. xlabel('时间t');
1. subplot(2,2,4);
2. plot(t_0,y_s,'r-',t,y(:,2),'-.');
3. diff = sum(abs(y_s - y(:,2)));
4. str1 = ['健康人数对比图s(t), 误差:',num2str(diff)];
5. title(str1);
6. legend('euler','ode','Location','Best');
7. ylabel('占人口比例%');
8. xlabel('时间t');
1.%解微分方程子程序(odefun函数方法)
2. function dydt = odefun(t,y,A,B)
3. dydt = zeros(2,1);
4. dydt(1) = A*y(1)*y(2) - B*y(1);
5. dydt(2) = -A*y(1)*y(2);
6. end