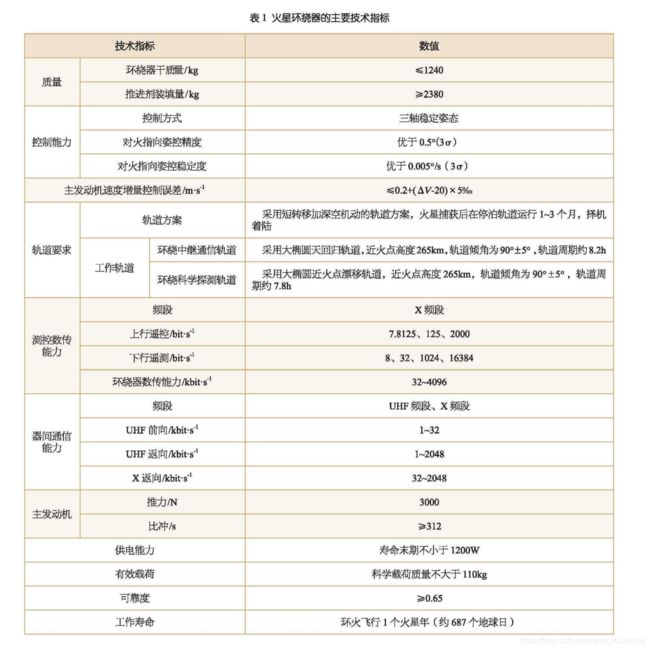
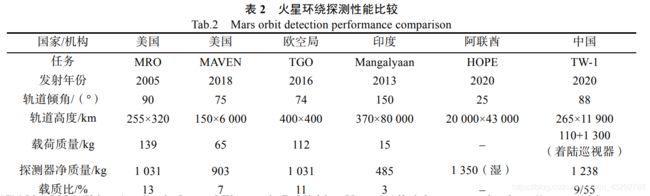
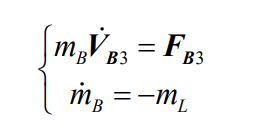2021深圳杯东三省建模

火星探测器着陆控制方案

本题聚焦于探测器从火星同步轨道出发到探测器在火星地表上
方悬停的过程（以下简称着陆过程），要求参赛队收集有关天问一号
探测器的音像和文字等公开资料，建立数学模型，研究如下问题：

1. 确定探测器着陆过程时间最短的操控方案（包括环绕器与着
   陆巡视器分离、阻尼伞打开、发动机系统点火等时间，以及
   发动机系统运行方案）；
2. 对给定的着陆过程时间，确定消耗能量最少的操控方案；
3. 如果希望探测器着陆过程与公开的音像和文字资料尽量一致，
   如何设计操控方案

相关数据及数据分析

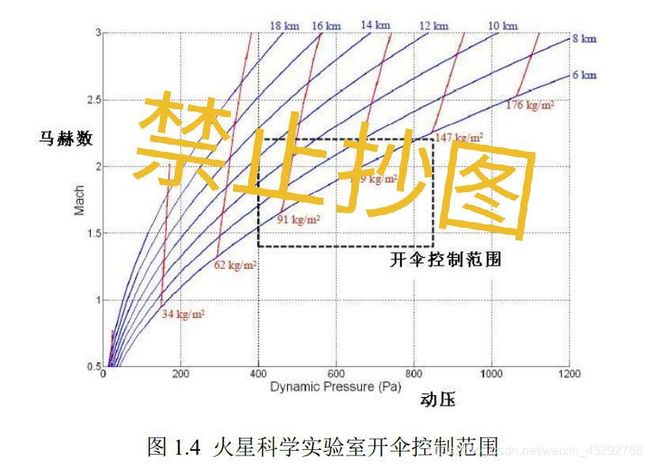
火星着陆器开伞条件均为超声速开伞，但为了确保降落伞的开伞可靠，
一般都控制开伞马赫数不大于 2.2；
 由于大气密度小，开伞动压较小，一般采用弹伞筒直接弹伞和一次开伞
技术；
 大部分火星着陆器均使用了盘缝带伞。其中在着陆前没有姿态控制的着
陆器均采用了火星探路者类型及其改进型的盘缝带伞（降落伞的稳定性高），在着陆前进行姿态控制的着陆器均采用海盗号类型的盘缝带伞（降落伞的阻力系数大）；

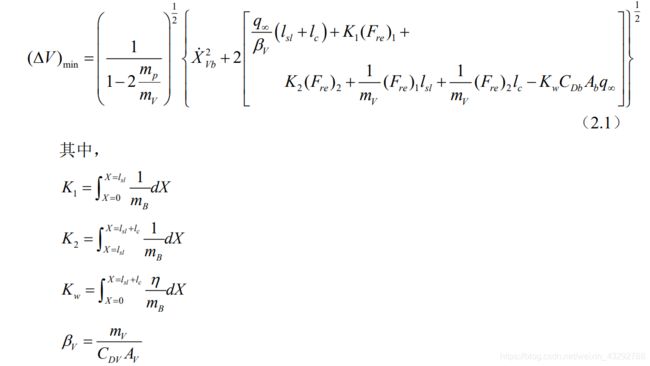
最小弹射分离速度的确定方法
对于降落伞系统而言，确定弹射分离速度非常关键。该弹射分离速度取得过小，将可能导致降落伞无法越过回收物的尾流或无法正常拉直；该弹射分离速度取得过大，由于弹射分离推力一般与该速度的二次方成正比，过大的弹射分离推力将导致弹伞载荷偏大，并对回收物的结构设计、降落伞连接分离机构的结构设计带来影响，从而导致更大的结构重量。选取合适的弹射分离速度，首先需要得到所需的最小弹射分离速度。

受力分析




过程一matlab程序：

clc,clear;
q=pi*22.62/180;
b=pi*150/180;
c=pi*25/180;
x=0;
y=0;
z=1752013;
r0=15000;
A=[1,0,0;0,0,1;0,-1,0];
B=[cos(q),sin(q),0;-sin(q),cos(q),0;0,0,1];
C=[1,0,0;0,cos(b),-sin(b);0,sin(b),cos(b)];
D=[-cos(c),-sin(c),0;sin(c),-cos(c),0;0,0,1];
E=A*B*C*D;
F=E';
X=F*[x,y,z]'; 
Q=X(1,1)/X(2,1);
if X(1,1)>0
 if X(2,1)>0
 a=atan(Q)*57.2957795131
 else 
 a=atan(Q)*57.2957795131+360
 end
else
 a=atan(Q)*57.2957795131+180
 end
r=r0+1737013; 
W=X(3,1)/r;
p=acos(W)*57.2957795131
q=pi*22.62/180;
b=pi*30/180;
c=pi*25/180;
x=1209430;
y=0;
z=1246800;
r0=0;
A=[1,0,0;0,0,1;0,-1,0];
B=[cos(q),sin(q),0;-sin(q),cos(q),0;0,0,1];
C=[1,0,0;0,cos(b),-sin(b);0,sin(b),cos(b)];
D=[-cos(c),-sin(c),0;sin(c),-cos(c),0;0,0,1];
E=A*B*C*D;
F=E';
X=F*[x,y,z]'; 
Q=X(1,1)/X(2,1);
if X(1,1)>0
 if X(2,1)>0
 a1=atan(Q)*57.2957795131
 else 
24
 a1=atan(Q)*57.2957795131+360
 end
else
 a1=atan(Q)*57.2957795131+180
 end
r=r0+1737013; 
W=X(3,1)/r;
p1=acos(W)*57.2957795131
i=a1-a;
j=p1-p;
I=19.51-i
J=44.12+j

过程二matlab代码：

%% 快速调整阶段的数值迭代求解。
clc;clear;close all;
Ve=2940;%比冲
g=3.72;  %火星重力加速度
h=600;%该阶段的下落距离
t=0; %初始时间
T=0.1;   %时间步长
M_temp=[];
V_temp=[];
shijian=[];
X_temp=[];
lisan=1500:100：7500;
%lisan=5000:5100;
for i = lisan
F=i;  %推力
%主减速阶段的末状态量作为快速调整阶段的初状态量
theta=55.6708*pi/180;%初速度与水平面的夹角
Vx0=32.23327;%水平初速度
Vy0=47.2005;  %竖直初速度
m0=1325.255;%初始质量
Ay0=g-F*sin(theta)/(m0-F/Ve*t);%竖直初加速度
Ax0=-F*cos(theta)/(m0-F/Ve*t);%水平初加速度
count=0; %计数器
X_res=Vx0*t+0.5*Ax0*t^2;
Y_res=Vy0*t+0.5*Ax0*t^2;
Result=[];

%% 迭代求 分解速度和分解位移
while (Y_res<h )
count=count+1;
Vx=Vx0+Ax0*T;
Vy=Vy0+Ay0*T;
Vx0=Vx;
Vy0=Vy;
X=Vx0*T+0.5*Ax0*T^2;
Y=Vy0*T+0.5*Ay0*T^2;
X_res=X_res+X;
Y_res=Y_res+Y;
 Time=count*T;
SIN=Vy/sqrt(Vy^2+Vx^2);
COS=Vx/sqrt(Vy^2+Vx^2);
Ay=g-F*SIN/(m0-F/Ve*Time);
Ax=-F*COS/(m0-F/Ve*Time);
Ax0=Ax;
Ay0=Ay;
end
M=m0-F/Ve*Time;%该阶段的末质量。
X_res; %水平位移
 Time=count*T;  %运动时间
 V_res=sqrt(Vx^2+Vy^2);%合速度
 jiaodu=atan(Vy/Vx)*180/pi; %末速度角度
 %Vx  %水平速度
M_temp=[M_temp;F/Ve*Time];
V_temp=[V_temp;V_res,Vx];
shijian=[shijian;Time];%记录运行时间
X_temp=[X_temp;X_res];
end
Answer=[lisan',M_temp,V_temp,shijian,X_temp];%结果总结在这里
subplot(221);
plot(lisan,M_temp,'LineWidth',2);
title('燃料消耗量关于推力变化图','FontSize',14);
xlabel('F_推（N）','FontSize',12);
ylabel('燃料消耗质量(千克)');

subplot(222);
plot(lisan,X_temp,'LineWidth',2);
title('水平位移关于推力变化图','FontSize',14);
xlabel('F_推（N）','FontSize',12);
ylabel('位移(米)');

subplot(223);
plot(lisan,V_temp(:,2),'LineWidth',2);
title('水平末速度关于推力变化图','FontSize',14);
xlabel('F_推（N）','FontSize',12);
ylabel('速度(米/秒)');

subplot(224);
plot(lisan,shijian,'LineWidth',2);
title('下落时间关于推力变化图','FontSize',14);
xlabel('F_推（N）','FontSize',12);
ylabel('时间(秒)');


%% 数据表格的写入。
M_temp=[];
V_temp=[];
shijian=[];
X_temp=[];
lisan=1500:7500;
for i = lisan
F=i;  %推力
%主减速阶段的末状态量作为快速调整阶段的初状态量
theta=55.6708*pi/180;%初速度与水平面的夹角
Vx0=32.23327;%水平初速度
Vy0=47.2005;  %竖直初速度
m0=1325.255;%初始质量
Ay0=g-F*sin(theta)/(m0-F/Ve*t);%竖直初加速度
Ax0=-F*cos(theta)/(m0-F/Ve*t);%水平初加速度
count=0; %计数器
X_res=Vx0*t+0.5*Ax0*t^2;
Y_res=Vy0*t+0.5*Ax0*t^2;
Result=[];

%% 迭代求 分解速度和分解位移
while (Y_res<h )
count=count+1;
Vx=Vx0+Ax0*T;
Vy=Vy0+Ay0*T;
Vx0=Vx;
Vy0=Vy;
X=Vx0*T+0.5*Ax0*T^2;
Y=Vy0*T+0.5*Ay0*T^2;
X_res=X_res+X;
Y_res=Y_res+Y;
 Time=count*T;
SIN=Vy/sqrt(Vy^2+Vx^2);
COS=Vx/sqrt(Vy^2+Vx^2);
Ay=g-F*SIN/(m0-F/Ve*Time);
Ax=-F*COS/(m0-F/Ve*Time);
Ax0=Ax;
Ay0=Ay;
end
M=m0-F/Ve*Time;%该阶段的末质量。
X_res; %水平位移
 Time=count*T;  %运动时间
 V_res=sqrt(Vx^2+Vy^2);%合速度
 jiaodu=atan(Vy/Vx)*180/pi; %末速度角度
 %Vx  %水平速度
M_temp=[M_temp;F/Ve*Time];
V_temp=[V_temp;V_res,Vx];
shijian=[shijian;Time];%记录运行时间
X_temp=[X_temp;X_res];
end
Answer=[lisan',M_temp,V_temp,shijian,X_temp];
%xlswrite('快速调整阶段各参数数据.xls',Answer);
%第一列是推力值
%第二列是燃料消耗量
%第三列是快速调整段末速度
%第四列是快速调整段的水平末速度
%第五列是运行时间
%第六列是水平位移

%%  最优轨迹图的绘制
figure;
M_temp=[];
V_temp=[];
shijian=[];
F=5085;  %推力
%主减速阶段的末状态量作为快速调整阶段的初状态量
theta=55.6708*pi/180;%初速度与水平面的夹角
Vx0=32.23327;%水平初速度
Vy0=47.2005;  %竖直初速度
m0=1325.255; %初始质量
Ay0=g-F*sin(theta)/(m0-F/Ve*t);%竖直初加速度
Ax0=-F*cos(theta)/(m0-F/Ve*t); %水平初加速度
count=0; %计数器
X_res=Vx0*t+0.5*Ax0*t^2;
Y_res=Vy0*t+0.5*Ax0*t^2;
Result=[];
G=[];
%% 迭代求 分解速度和分解位移
while (Y_res<h )
count=count+1;
Vx=Vx0+Ax0*T;
Vy=Vy0+Ay0*T;
Vx0=Vx;
Vy0=Vy;
X=Vx0*T+0.5*Ax0*T^2;
Y=Vy0*T+0.5*Ay0*T^2;
X_res=X_res+X;
Y_res=Y_res+Y;
 Time=count*T;
G=[G;X_res,Y_res,V_res,Time];
SIN=Vy/sqrt(Vy^2+Vx^2);
COS=Vx/sqrt(Vy^2+Vx^2);
Ay=g-F*SIN/(m0-F/Ve*Time);
Ax=-F*COS/(m0-F/Ve*Time);
Ax0=Ax;
Ay0=Ay;
end
plot(G(:,1),3000-G(:,2),'k','LineWidth',2);
title('快速调整段运动轨迹','FontSize',15);
xlabel('X轴/(m)');
ylabel('Y轴/(m)');

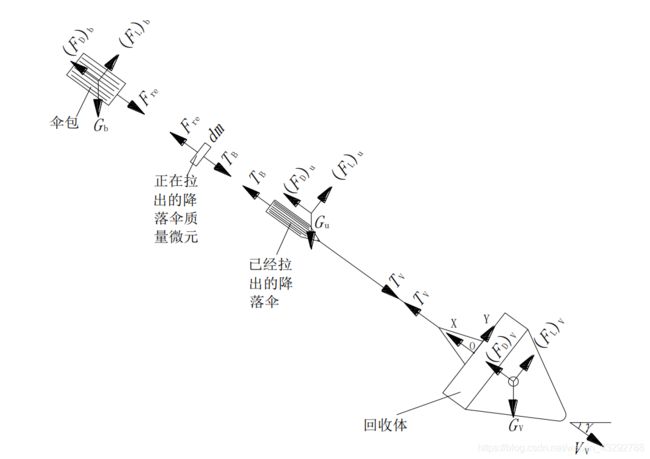
阻尼伞打开的数学模型为：
对阻尼伞进行受力分析，及阻尼伞打开需要考虑的因素
matlab部分程序

%% 计算粗避障阶段最大的下落时间。
clc;clear;
syms V0 g t1;
V0=0.24183;  %竖直初速度
%t1=53;%无推力落体下落时间t1
g=3.72;
%无推力落体下落最大时间T_max
T_max=double(solve(V0*t1+0.5*g*t1^2-2300))