PyTorch-05神经网络与全连接（Logistic Regression、交叉熵、交叉熵来优化一个多分类的问题、全连接层（MLP网络层）、激活函数与GPU加速、测试、Visdom可视化）

PyTorch-05神经网络与全连接（Logistic Regression逻辑回归、交叉熵、交叉熵来优化一个多分类的问题、全连接层（MLP网络层）、激活函数与GPU加速、测试（validation performance）、Visdom可视化）

一、Logistic Regression逻辑回归

Logistic Regression现在完全被classification分类的相关概念给代替掉了。

这里先回顾一下linear regression

linear regression是一个非常简单的线性模型 y = xw + b 。其中输入是x，网络参数w和b，输出值是一个连续的y值。因为输出y是连续型的，所以称其为regression。

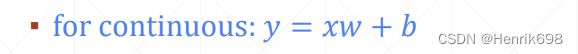
如何将这个regression转为classification呢？
这里我们添加一个激活函数σ，即 y = σ(xw + b)。其中σ：sigmoid or logistic。

通过sigmoid函数后会将连续型的y值，压缩至[0,1]这个区间，即概率值（如果这个概率P越接近0，则输出为0表示不是；如果这个概率P越接近1，则输出为1表示是）。因此这样就可以理解为是一个classification的问题。

二分类 Binary Classification

就是通过sigmoid函数将输出值y压缩至0到1这个区间范围内再输出。输出结果越接近0，则分类为0；如果输入结果越接近1，则分类为1。

经过σ处理的过程就是logistic function。

分类与回归的区别：目标Goal v.s. 方法Approach

对于回归类型：
目标：预测值 = 真实值
方法：minimize dist 最小距离，即预测值Pred与真实值y的差距。这个差距是用范数来表示，可以使用2范数的平方 || pred - y ||₂ ² 来表示。 2范数为：|| pred - y ||₂ 2范数是要开根号的，所以mse就是对2范数增加一个平方以抵消开的根号。

对于分类类型：
目标：使得准确性accuracy很高，最大化的基准maximize benchmark。
分类型并不直接优化accuracy。(accuracy可以理解为有五个数字，预测对了3个，accuracy=3\5)
方法1：minimize dist 最小距离，只不过这里的预测值是(|)和真实值r(|)的最小距离，使得=r，这里的x是相同的。
方法2： minimize divergence 最小分歧，预测值是(|)和真实值r(|)的差别最小。

Q1. why not maximize accuracy? 为什么不是求得最大准确度？为什么不能使用accuracy做训练？

accuracy = ∑ (==) / () = 预测对的数量 / 总的数量
比如：二分问题，有5个数字，预测对了3个，accuracy = 3 / 5 = 60%

这里要讨论两种情况：
由于accuracy会存在以下两种情况，所以accuracy不用做训练比较好。

**情况1、**比如预测第三个数字时，预测错了，本来预测的是0.4，这样由于2分类情况，0.4没有大于0.5，所有预测为0；但是实际情况是1。通过调节w权值，使得预测的0.4变成了0.45，这个概率probability增加了0.05，更加靠近真实值1了。但是，因为没有大于0.5这个二分类阈值，使得没有发生本质变化，所以accuracy没有变化。因此这就会产生一种情况，w权值在改变，但是我们的accuracy没有变化，所以∂acc / ∂w为0，即梯度gradient = 0。

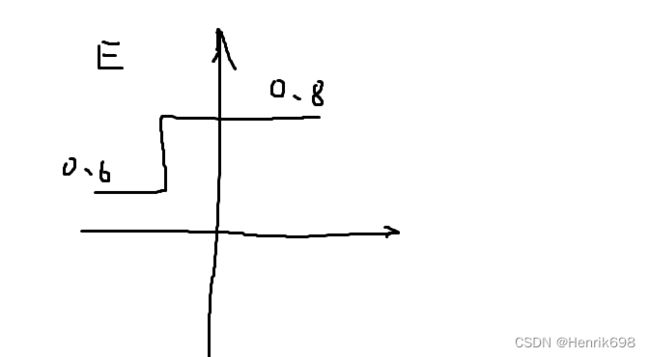
**情况2、**比如预测第三个数字时，预测的概率为0.499，当w权值改变一点点时，预测由0.499变为了0.501。这使得概率大于了0.5二分类的阈值。所以原本是预测错的0，因为w的变化非常小，从而就使得预测正确了1。使得我们的accuracy从之前的预测对了3个，变成了预测对了4个。使得accuracy = 4 / 5 = 80%。由于w权值只增加了很小的数，比如0.001，但是accuracy从60%变到80%，增加了20%。这样0.2 / 0.001 会得到一个非常大的值，使得梯度gradient不在连续或者梯度很大，使得梯度爆炸的情况产生。如下图

Q2. why call logistic regression？为什么叫逻辑回归

logistic 是因为使用sigmoid函数作为激活函数。

regression 这个是有一定争议的：（这里我们不必过多浪费时间考虑这个，因为logistic regression目前基本用不到了）
▪ MSE => regression
如果MSE作为loss的时候，(预测值-真实值)^2我们希望预测值越接近真实值越好，probability概率是一个连续的，所以会有regression的情况。
▪ Cross Entropy => classification
如果使用cross entropy交叉熵损失函数这种作为loss，我们可以理解为是一个classification的问题。

Binary Classification 二分类

概率大于0.5预测为1，小于0.5预测为0。

如果损失函数是minimize MSE均方误差，我们可以理解为是regression问题。

Multi-class classification 多分类

对于多分类有一个约束条件，就是所有分类概率之和为1。
对于这个约束我们应该如何生成呢？

使用Softmax函数：这个函数可以满足上面多分类的约束条件。

这个函数输出的所有概率之和为1，这个softmax函数还有一个重要特点，就是会将原来输入较大的通过函数输出后会放的更大，而原来较小的则会压缩到较为密集的空间，这样会使得原来最大与最小值之间的差价通过该函数而扩大（输入中2/1=1,输出概率中0.7/0.2=3.5，这个明显扩大了）。

二、交叉熵

损失函数 Loss for classification

▪ MSE
▪ Cross Entropy Loss
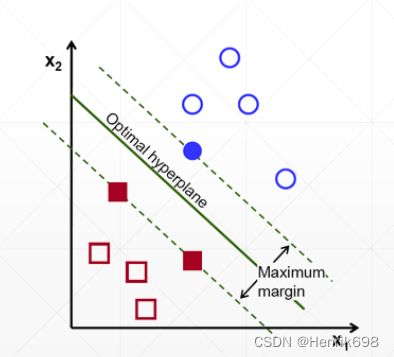
▪ Hinge Loss 在svm中使用比较多，会惩罚margin，margin小于1就会惩罚margin。

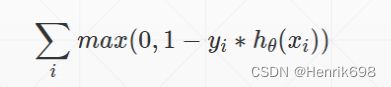
熵 Entropy

▪ Uncertainty 不确定性，不稳定性
熵越大越稳定。
▪ measure of surprise 惊喜的度量

▪ higher entropy = less info.

Entropy是衡量p一个分布的其本身的稳定度：

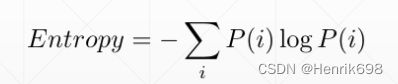
例子：中彩票 Lottery

import torch
from torch.nn import functional as F

#中奖概率是相等的
a = torch.full([4],1/4)
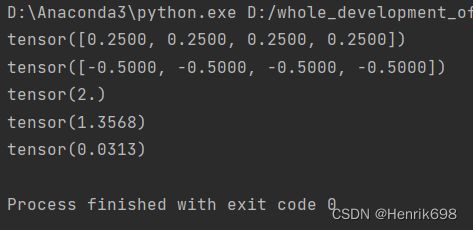
print(a)

#分布的entropy
#p乘以以2为底的log的1/p
print(a*torch.log2(a))
#获得熵，熵越大越稳定，说明没有惊喜度
print(-(a*torch.log2(a)).sum())

#另一组中奖概率,有一个概率比其他的高
b = torch.tensor([0.1,0.1,0.1,0.7])
#获得熵，熵有所下降，说明有惊喜
print(-(b*torch.log2(b)).sum())

#另一组极端中奖情况，有一个概率比其他高的多
c = torch.tensor([0.001,0.001,0.001,0.999])
#熵非常低，意味着会非常惊喜
print(-(c*torch.log2(c)).sum())

交叉熵 Cross Entropy

交叉熵Cross Entropy是衡量两个分布p和q的不稳定度：

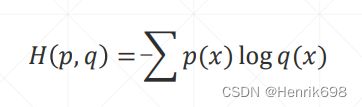
上面的式子展开：
H§ + KL Divergence散度 （Kullback-Leibler divergence越小p和q重合区域越多，p和q越接近。）

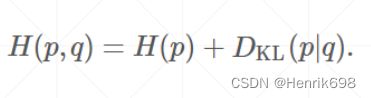
关于散度，下图两个Gaussian distribution的曲线，左图曲线重合区域比较小（阴影部分），假设Dkl = 2。右图两个高斯分布曲线相互重合，则Dkl ≈ 0。

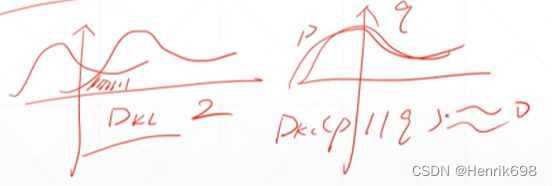
p分布非常不稳定，则熵接近于0，熵接近0说明是不稳定的情况；
p分布与q分布相互重合，则Dkl接近于0，Dkl接近0说明两个分布接近于0。

特殊情况：
当P = Q的时候
交叉熵公式：
H(p,q) = H§ + Dkl(p|q)
Dkl(p|q) ≈ 0
所以 H(p,q) = H§
即 交叉熵 = 熵

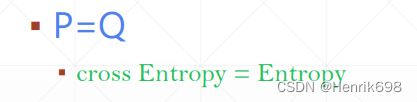
当对于one-hot encoding独热编码的时候
[0, 0, 0, 1, 0]
将1带入熵的公式中，-1log1
log1 = 0
所以H§的Entropy = 0
所以H(p,q) = Dkl(p|q)
cross entropy 对于0和1分布独热编码进行衡量的指标就是KL divergence。
KL divergence就说明：如果 cross entropy接近0，KL divergence就接近于0。间接的Dkl为0，按照上面的那种情况，则H(p,q) = H§。就说明p和q的分布就越来越接近。
q(y|x) 预测 与 p(y|x)真实 的Dkl接近于0，p与q就越接近。

Binary Classification对于二分类的问题，cross entropy应该如何运算：

H(P,Q) = - ∑ P(i)logQ(i) i=(cat,dog)
H(P,Q) = - P(cat)logQ(cat) - P(dog)logQ(dog)
由于是二分类，P(dog) = (1 - P(cat))
H(P,Q) = - P(cat)logQ(cat) - (1 - P(cat))log(1 - Q(cat))
P(cat)为真实值y，Q(cat)为神经网络预测概率p
H(P,Q) = - (ylog§ + (1 - y)log(1 - p))

当y = 1时，H(P,Q) = -ylog§，需要最小值-ylog§，即最大化log§，最大化p = p(y=1|x)；
当y = 0时，H(P,Q) = -log(1 - p)，需要最小值-log(1 - p)，即最大化log(1 - p)，最小化p = p(y=0|x)

for example例子：

P1 = [ 1, 0, 0, 0, 0 ]为真实概率分布情况；
Q1 = [ 0.4, 0.3, 0.05, 0.05, 0.2]为神经网络输出的概率分布情况。
cross entropy为：H(P1,Q1) = -(1log0.4 + 0log0.3 + 0log0.05 + 0log0.05 + 0log0.2) = -log0.4 ≈ 0.916

我们想要的预测情况：Q1 = [ 0.98, 0.01, 0, 0, 0.01 ]
cross entropy为：H(P1,Q1) = -∑ P1(i)logQ1(i) = -(1log0.98 + 0log0.01 + 0log0 + 0log0 + 0log0.01) = -log0.98 ≈ 0.02

可以发现cross entropy从原来的0.916下降到0.02，说明预测值Q1越来越接近真实值P1。

why not use MSE? 对于分类问题，为什么不使用MSE，而是用cross entropy

▪ sigmoid和MSE搭配使用很容易出现sigmoid饱和的情况，即梯度离散（gradient vanish梯度消失），这样串联起来会非常困难。
▪ cross entropy的梯度信息更大，收敛的更快，MSE相对收敛要慢一些converge slower
▪ 但是有些时候并不绝对，在做一些前沿算法的东西时（比如：meta-learning），cross entropy如果不行，最好试一下MSE，因为MSE的导数非常简单，即(p-y)^2’ = 2(p-y)。

数值稳定性Numerical Stability(cross entropy小案例)

import torch
from torch.nn import functional as F

x = torch.randn(1,784)
w = torch.randn(10,784)

logits = x@w.t()
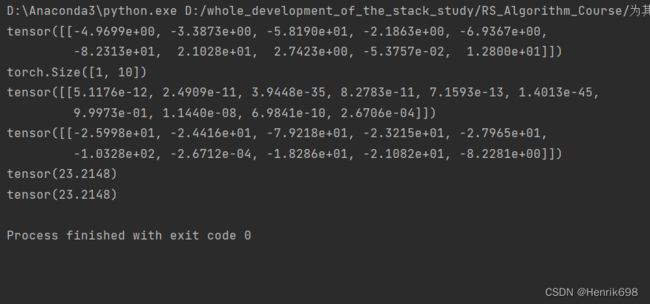
print(logits)
print(logits.shape)

pred = F.softmax(logits,dim=1)
print(pred)

pred_log = torch.log(pred)
print(pred_log)

#pytorch中cross entropy是将log与softmax打包到一起了，所以如果使用cross_entropy参数就必须使用logits。
#如果传入了predic的话，predict已经经过softmax了，出入cross_entropy中又会经过一遍softmax，会使得结果非常小。
#cross_entropy这个函数 = softmax这个操作 + log操作 + nll_loss操作
a=F.cross_entropy(logits,torch.tensor([3]))
print(a)

#如果一定要自己计算,就需要传入pred经过log处理过后的
b=F.nll_loss(pred_log,torch.tensor([3]))
print(b)

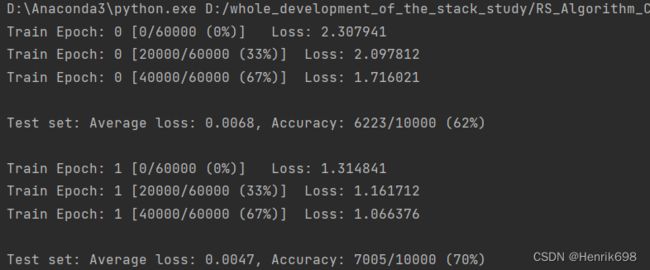
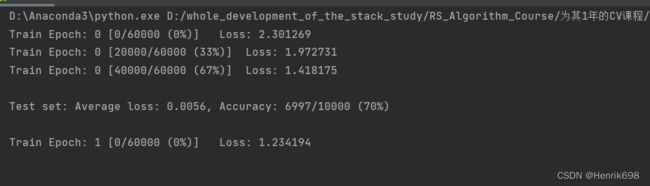
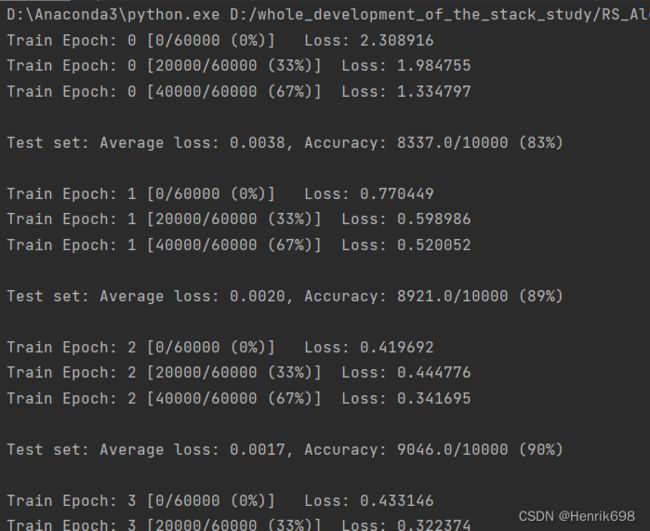
三、交叉熵来优化一个多分类的问题

有10层，代表有10分类：

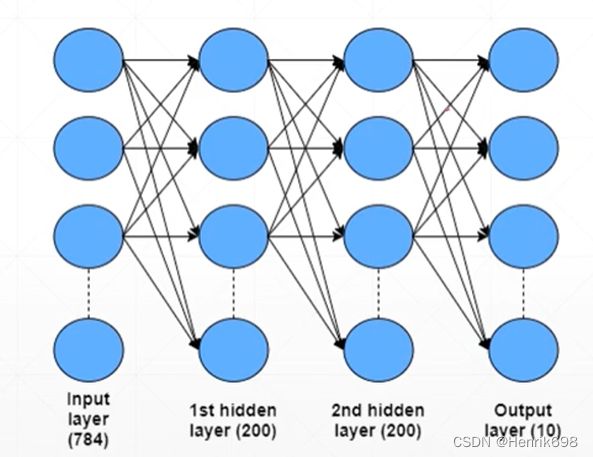
由于还没有讲解线性层，所以这里使用一些底层的操作，方便大家对pytorch梯度计算的过程有一个非常深刻的认识。

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms

#3、定义一个优化器
#这个优化器优化的目标是三组全连接层的变量[w1, b1, w2, b2, w3, b3]
batch_size=200
learning_rate=0.01
epochs=10

#加载数据
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)


#1、完成网络tensor的定义：
#新建立三个线性层，每个线性层都有w(tensor)和b(tensor):
#首先参数1为输出维度200。
#参数2为输入维度784=28*28，可以理解为从784降维到200的过程。
#参数3必须要指定requires_grad否则会报错。
w1, b1 = torch.randn(200, 784, requires_grad=True),\
         torch.zeros(200, requires_grad=True)
w2, b2 = torch.randn(200, 200, requires_grad=True),\
         torch.zeros(200, requires_grad=True)
w3, b3 = torch.randn(10, 200, requires_grad=True),\
         torch.zeros(10, requires_grad=True)

#何同学的初始化点
#初始化很重要，如果没有这个初始化，则该运算结果会程序梯度离散的问题，loss会一致保持不变
torch.nn.init.kaiming_normal_(w1)
torch.nn.init.kaiming_normal_(w2)
torch.nn.init.kaiming_normal_(w3)

#2、完成网络forward的过程：
def forward(x):
    x = x@w1.t() + b1 #这里b1会完成一个boardcasting的操作
    x = F.relu(x) #激活函数使用relu()
    x = x@w2.t() + b2
    x = F.relu(x)
    x = x@w3.t() + b3
    x = F.relu(x)
    # 这里的x就是logits，即没有经过sigmoid，也没有经过softmax的东西叫做logits。
    # 一般来说，这里最后一层的relu()应该是不许用的，只要不使用softmax和sigmoid函数就行。
    return x

optimizer = optim.SGD([w1, b1, w2, b2, w3, b3], lr=learning_rate)
criteon = nn.CrossEntropyLoss()

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)

        logits = forward(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        logits = forward(data)
        test_loss += criteon(logits, target).item()

        pred = logits.data.max(1)[1]
        correct += pred.eq(target.data).sum()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

可以发现loss下降了。

四、全连接层（MLP网络层）

实践Be practical:

直接写一个三层的全连接层：
这里的layer三层是分开写的：

import torch
import torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms

x = torch.rand(1,784)
# print(x)
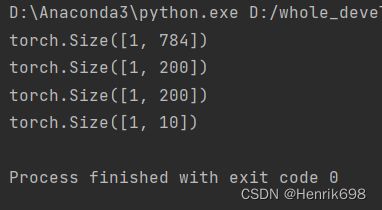
print(x.shape)

layer1 = nn.Linear(784,200)
layer2 = nn.Linear(200,200)
layer3 = nn.Linear(200,10)

x = layer1(x) #降维过程[1,784]->[1,200]
x = F.relu(x,inplace=True) #激活函数relu
print(x.shape)

x = layer2(x) #特征提取过程[1.200]->[1,200],没有降维过程所以维度不变。
x = F.relu(x,inplace=True) #激活函数relu
print(x.shape)

x = layer3(x) #输出层，会从[1,200]->降维到[1,10]
x = F.relu(x,inplace=True) #激活函数relu
print(x.shape)

pytorch中的两种接口的API（nn.ReLU v.s. F.relu()）

▪ class-style API
类风格的API，都存在nn中，即nn.ReLU；风格是名字大写。

x1=torch.rand([1,10])
print(x1.shape)

x2 = x1

layer = nn.ReLU() #实例化
y2 = layer(x2)
print(y2)

▪ function-style API
函数型API，可以很好管理中间运算过程，只是使用了GPU加速的这个功能。F.relu F.cross-entropy

x1=torch.rand([1,10])
print(x1.shape)

y1 = F.relu(x1, inplace=True)
print(y1)

创建一个模型类

实际上我们自己能够实现一个nn.Module的话，将三层创建到一起，会使得类的封装性变得更强。这个类就代表着网络结构，可以其一个对应的名字。

如果要创建自己的网络结构的话：
▪ inherit from nn.Module这个网络结构要继承自nn.Module；nn.Module会带来许多方便性。
▪ init layer in init 实现初始化函数，并带上必要的参数。
▪ implement forward() 需要实现forward，不需要实现backward，backward是nn.Module会自动提供的，向后求导的过程也不需要额外去写公式告诉pytorch如何向后求导，pytorch autograd的包会自动完成向后求导的功能，写好向前的功能之后，会自动记录向前传播的过程，然后使用自动求导的工具，要自动完成当前继承图的向后传播的过程。

如果要新建一个自己的层：
这里的layer三层是组合在class类中的

#类名(继承nn.Module)
class MLP(nn.Module):
    #初始化方法，需要带一些自己的参数就可以，不需要给nn.Module传参数，不需要带参数也是可以的。
    def __init__(self):
        super(MLP,self).__init__()
        #这里不需要带参数，因为已经给好维度了[784,200]。
        #如果要给参数，注意一定要上下相互能配合的上。
        self.model = nn.Sequential(
            nn.Linear(784,200),
            nn.ReLU(inplace=True),
            nn.Linear(200,200),
            nn.ReLU(inplace=True),
            nn.Linear(200,10),
            nn.ReLU(inplace=True),
        )

    def forward(self,x):
        x = self.model(x) #这句话使用了module.forward函数。
        return x

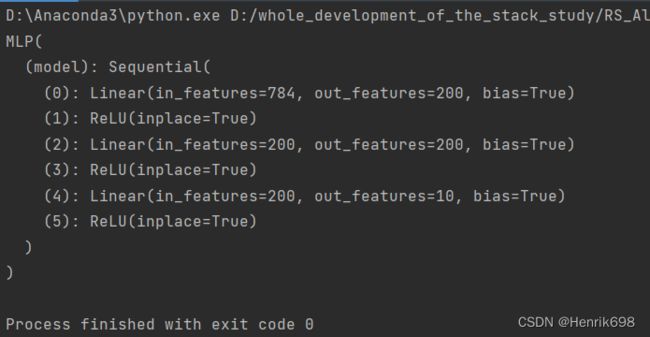
a = MLP()
print(a)

完整的引用自己创建class类模型的实例：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms

batch_size=200
learning_rate=0.01
epochs=10

#加载数据
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)


#类名(继承nn.Module)
#使用nn接口会有一套它自己的初始化方法。
class MLP(nn.Module):
    #初始化方法，需要带一些自己的参数就可以，不需要给nn.Module传参数，不需要带参数也是可以的。
    def __init__(self):
        super(MLP, self).__init__()
        # 这里不需要带参数，因为已经给好维度了[784,200]。
        # 如果要给参数，注意一定要上下相互能配合的上。
        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.ReLU(inplace=True),
            nn.Linear(200, 200),
            nn.ReLU(inplace=True),
            nn.Linear(200, 10),
            nn.ReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x) #这句话使用了module.forward函数。

        return x

net = MLP()
#优化器
#参数net.parameters()，直接继承nn,可以方便管理[w1, b1, w2, b2, w3, b3...]，不需要自己来管理了。
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss()

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)

        logits = net(data)
        loss = criteon(logits, target)
		
		#这三个函数的作用是先将梯度归零（optimizer.zero_grad()），然后反向传播计算得到每个参数的梯度值（loss.backward()），最后通过梯度下降执行一步参数更新（optimizer.step()）
        optimizer.zero_grad() #先将梯度归零
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        logits = net(data)
        test_loss += criteon(logits, target).item()

        pred = logits.data.max(1)[1]
        correct += pred.eq(target.data).sum()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

五、激活函数与GPU加速

激活函数：

sigmoid函数 和 Tanh函数

蓝色的是sigmoid函数，范围是0到1，sigmoid存在一个问题，就是梯度离散，当w在左侧的时候梯度接近于0，当w在右侧的时候梯度接近于0，因此现在不适用sigmoid函数。

Tanh函数是经过sigmoid函数缩放平移后的函数，区间是-1到1。Tanh函数也会存在梯度离散，但是Tanh函数在RNN循环神经网络中会用的多一些。

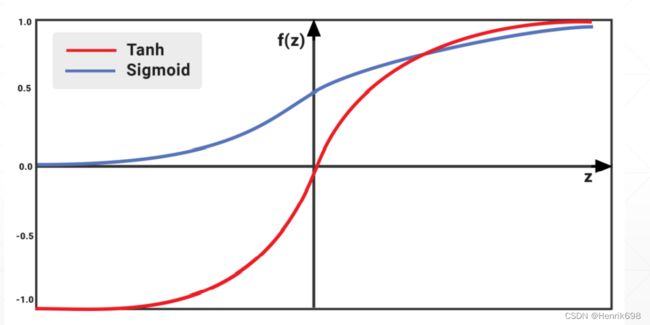
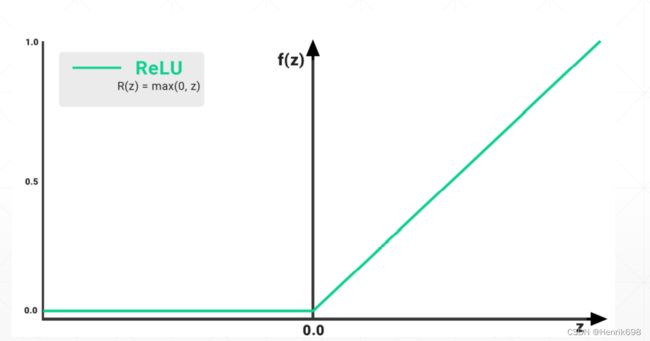
ReLU函数

ReLU函数更简单，当阈值小于某一个值的时候，这里阈值时0，就不响应，当x>0的时候，输出值就是y=x。从数学上来说ReLU函数在x=0处不连续，但不影响，一般来说我们对于x=0这个点的梯度理解为0或者理解为1。
ReLU函数解决了sigmoid函数梯度离散的现象。ReLU函数对于x>1的时候，∂y/∂x = 1，这个是非常有利于串型的传播，即没有对原来的梯度进行放大或减小，就不会出现梯度离散或者梯度爆炸的情况。

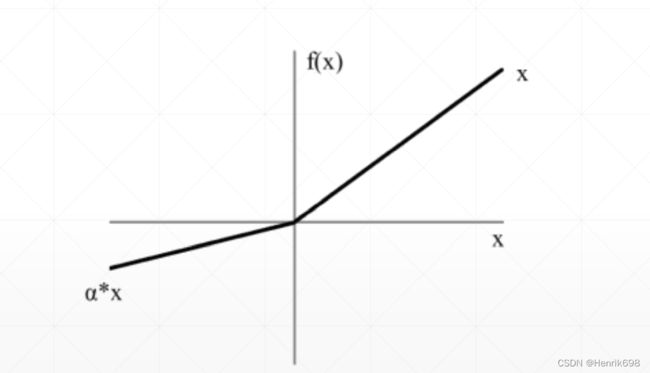
Leaky ReLU函数

Leaky ReLU函数，x<0，y = αx 这个α斜率在pytorch可以设置。避免当x<0，梯度信息全部为0了，让其在x<0这个区间能够得到较小的梯度，也能返回到搜索的最优解，避免x<0的梯度信息全部为0，使得搜索卡在原地不动了。

Leaky ReLU函数pytorch中的使用：

import torch
import torch.nn as nn

a = torch.rand(1,10)
print(a.shape)

layer = nn.LeakyReLU()
res = layer(a)
print(res)

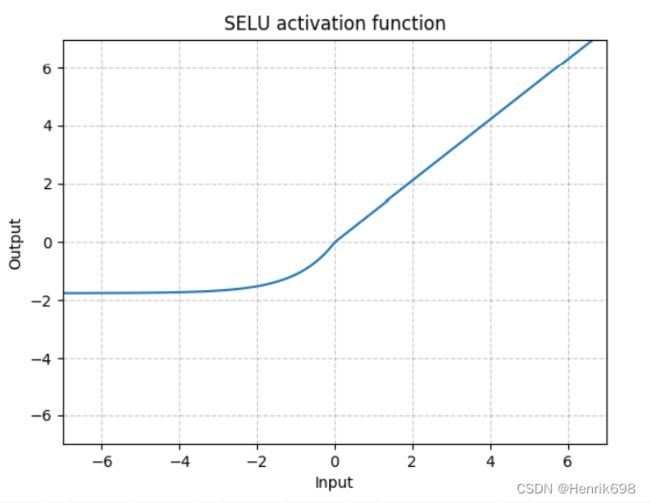
SELU函数

ReLU函数在x = 0处数学上是不连续的。一种更加光滑的曲线SELU函数。
SELU函数是两个函数的concat组合，x>0的部分是ReLU函数，x<0的部分是指数函数。

目前SELU函数用到的比较少，Leaky ReLU还是有些需要用到的：

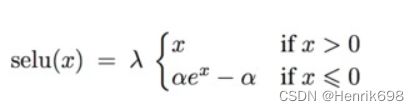
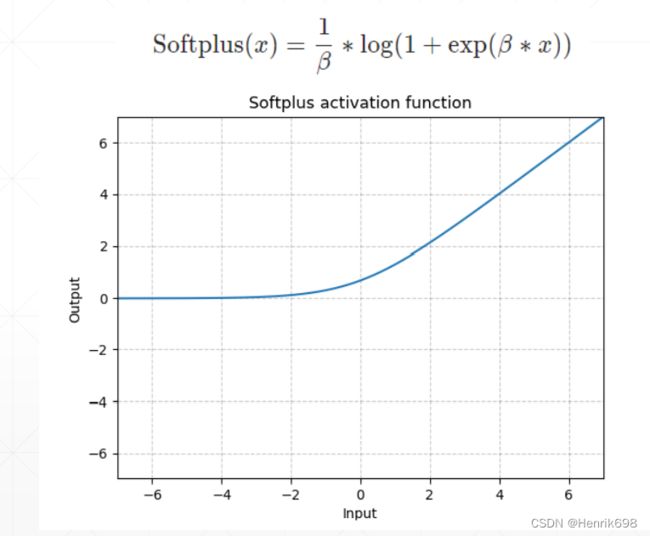
softplus 函数

使得x=0处梯度也能均匀变化的过程，是ReLU函数平滑的一个版本，x=0附加不在是不连续的了。softplus函数使用比较少。

GPU加速

下面代码只是简单告诉如何设置GPU加速：

device = torch.device('cuda:0') #这里的0表示cuda的编号，如果有8张显卡，就可以是0~7这样的编号。
net = MLP().to(device) #.to(device)就可以将模块搬到GPU或CPU上面去。
optimizer = optim.SGD(net.parameters(), lr = learning_rate)
criteon = nn.CrossEntropyLoss().to(device) #loss层也是可以搬上去的

for epoch in range(epochs):
	for batch_idx, (data, target) in enumerate(train_loader):
		data = data.view(-1,28*28)
		data, target = data.to(device), target.cuda() #注意data也要搬运，.to(device)是0.4或1.0版本推荐的方法，而.cuda()是以前0.3版本的方法不推荐，不好控制。

#这里需要注意：对于模块的net = MLP().to(device)，当device改变时，该模块也会原地更新到新的device上，原来的会消失。而对于tensor，data.to(device)，这里当device改变时，会在新的device上产生一个tensor，并且原来的tensor不消失，即CPU和GPU上都有该tensor。

实例代码：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms


batch_size=200
learning_rate=0.01
epochs=10

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)






class MLP(nn.Module):

    def __init__(self):
        super(MLP, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 10),
            nn.LeakyReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x)

        return x

device = torch.device('cuda:0')
net = MLP().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss().to(device)

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)
        data, target = data.to(device), target.cuda()

        logits = net(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        data, target = data.to(device), target.cuda()
        logits = net(data)
        test_loss += criteon(logits, target).item()

        pred = logits.data.max(1)[1]
        correct += pred.eq(target.data).sum()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

当代码运行时：

GPU利用率明显提高了：

六、测试（validation performance）

deep learning并不是越train训练越好，会存在over fitting过拟合的情况。数据量以及架构是训练的核心问题。
下图中的test是通过validation test来做的。黄色线的accuracy在后面不在上升，而且在loss中黄色线后面波动的很厉害。

比较预测结果与真实值的准确性accuracy（即预测正确的数量占比）

这里使用argmax方法，argmax返回的是最大数的索引.argmax有一个参数axis,默认是0,表示第几维的最大值。

import torch
from torch.nn import functional as F

logits = torch.rand(4,10)
# print(logits)

pred = F.softmax(logits,dim=1) #对每一行进行softmax
# print(pred)
print(pred.shape)

# pred2 = F.softmax(logits,dim=0) #对每一列进行softmax
# print(pred2)

pred_label = pred.argmax(dim = 1) #argmax()取出a中元素最大值所对应的索引
print(pred_label)

logits_label = logits.argmax(dim=1)
print(logits_label)

#真实的label
true_label = torch.tensor([9,3,2,4])

correct = torch.eq(pred_label,true_label)
print(correct)

print(correct.sum().float())
print(correct.sum().float().item()/4) #.item()是取出数值

when to test 什么时候应该计算test performance（或称为validation performance）

首先不能每做完一个batch就做一次test performance，会花费大量时间做test，这样时不太合理的，尤其是一些大型数据集，会花费大量时间。
基本上，每完成一些batch后做一次test performance。
或则，每完成一些epoch后做一次test performace。

一个计算accuracy的代码示例：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms


batch_size=200
learning_rate=0.01
epochs=10

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)



class MLP(nn.Module):

    def __init__(self):
        super(MLP, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 10),
            nn.LeakyReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x)

        return x

device = torch.device('cuda:0')
net = MLP().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss().to(device)

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)
        data, target = data.to(device), target.cuda()

        logits = net(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        data, target = data.to(device), target.cuda()
        logits = net(data)
        test_loss += criteon(logits, target).item()

        pred = logits.argmax(dim=1)
        correct += pred.eq(target).float().sum().item()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

七、Visdom可视化，检测数据动态变化

有利于调试，找到问题所在的可视化工具：Visdom可视化

TensorBoardX

实时变量的曲线，查看模型的架构，查看二维照片，降维可视化的过程。

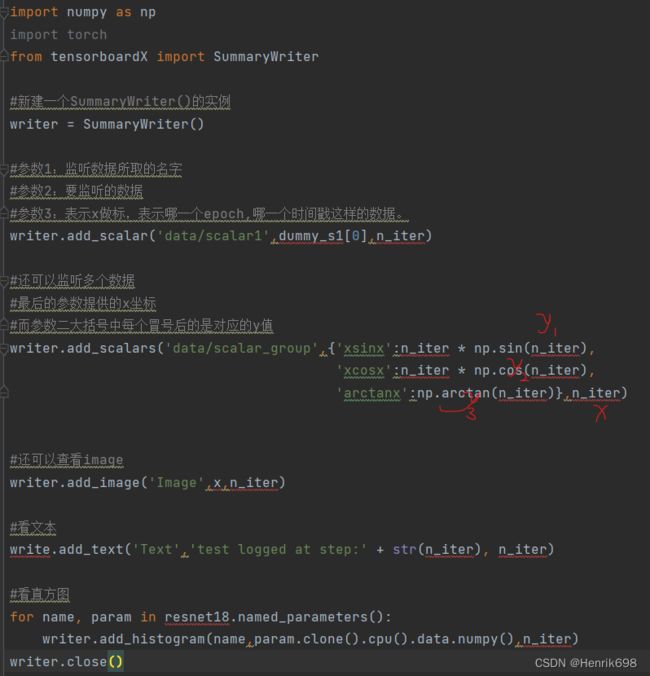
TensorboardX在pytorch中的使用：
注意：tensorboard抽取的是一个numpy的数据，如果跟tensor直接进行match的话，必须将tensor转换到cpu()上面，然后.numpy()转成numpy数据，才能赋值给tensorboard进行可视化。

import numpy as np
import torch
from tensorboardX import SummaryWriter

#新建一个SummaryWriter()的实例
writer = SummaryWriter()

#参数1：监听数据所取的名字
#参数2：要监听的数据
#参数3：表示x做标，表示哪一个epoch,哪一个时间戳这样的数据。
writer.add_scalar('data/scalar1',dummy_s1[0],n_iter)

#还可以监听多个数据
#最后的参数提供的x坐标
#而参数二大括号中每个冒号后的是对应的y值
writer.add_scalars('data/scalar_group',{'xsinx':n_iter * np.sin(n_iter),
                                        'xcosx':n_iter * np.cos(n_iter),
                                        'arctanx':np.arctan(n_iter)},n_iter)

#还可以查看image
writer.add_image('Image',x,n_iter)

#看文本
write.add_text('Text','test logged at step:' + str(n_iter), n_iter)

#看直方图
for name, param in resnet18.named_parameters():
    #注意：tensorboard抽取的是一个numpy的数据，如果跟tensor直接进行match的话，必须将tensor转换到cpu()上面，然后.numpy()转成numpy数据，才能赋值给tensorboard进行可视化。
    writer.add_histogram(name,param.clone().cpu().data.numpy(),n_iter)
writer.close()

Visdom from Facebook

Visdom与tensorboard完成的风格是不同的，Visdom可以原生的接受tensor。

Step 1. install
pip install visdom -i http://pypi.douban.com/simple/ --trusted-host pypi.douban.com

Step 2. run server damon
开启监听功能，Visdom实际上是一个web服务器， 开启web服务器以后，向这个服务器丢数据，之后就会 将这些数据渲染出来到网页上面。确保在运行程序之前开启了Visdom的服务器。

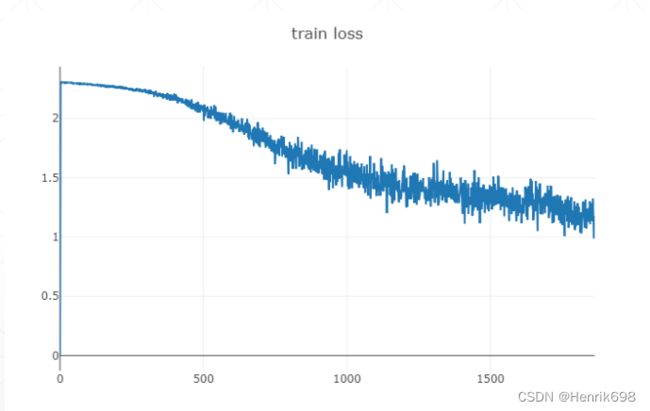
visdom提供绘制线 lines：single trace 单一追踪

from visdom import Visdom

#绘制一条曲线
viz = Visdom() #创建一个实例

#创建一条直线，再把最新数据添加到这条直线上面。
#第一步：先创建一条直线
#参数1：y
#参数2：x
#参数3：win表示这个直线的唯一标识符，即id
#在visdom中还有一个是工程的id,每个工程包含许多win,这个参数叫做environment，如果environment不指定，则env='main',即默认的大环境。
#参数4：是这个窗体的额外信息，比如title命名为‘train loss’
viz.line([0.],[0.],win = 'train_loss', opts=dict(title = 'train loss'))

#第二步：将数据逐步的添加进来。
#参数1：对于非image数据的话，传入的还是numpy类型。
#参数update：这里一定要指定为‘append’，是逐步添加到图上并且不覆盖原先添加的，如果不写这个参数，则会覆盖原来的数据。
viz.line([loss.item()],[global_step],win = 'train_loss',update='append')

这个刷新率是非常快的，每1秒返回一次。不像Tensorboard每30秒刷新一次。

visdom提供绘制线 lines: multi-traces 多追踪
我们可能会同时查看train loss 和 test loss 就需要multi-traces。

from visdom import Visdom

#绘制多条曲线
viz = Visdom() #创建一个实例

#参数1：[y1,y2]需要同时传入两个数值。
#参数2：x
#参数3：win窗体的唯一标识符
#参数4：是这个窗体的额外信息，legend是list，表示y1和y2的图标。
viz.line([[0.0,0.0]],[0.],win = 'test',
         opts = dict(title='test loss&acc.',legend = ['loss','acc.']))

#参数1：[test loss, accuracy]
#参数update：这里一定要指定为‘append’。
viz.line([[test_loss, correct/len(test_loader.dataset)]],
         [global_step],win = 'test',update='append')

visdom提供的可视化功能 visual X

from visdom import Visdom

#可视化功能
viz = Visdom() #创建一个实例

#data是一个image,其shape是[b,1,28,28]这样一个tensor,不需要转成numpy数据
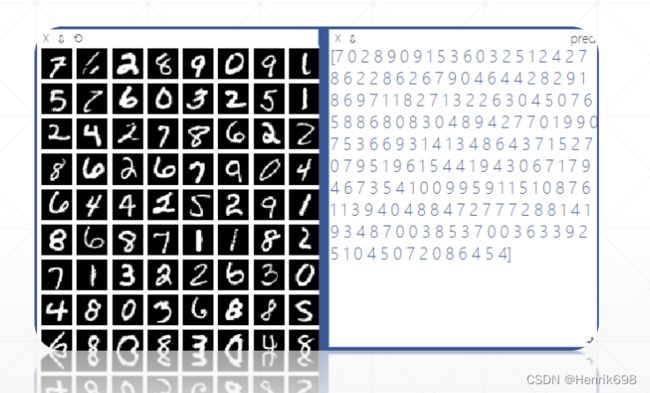
viz.images(data.view(-1,1,28,28),win = 'x')

viz.text(str(pred.detach().cpu().numpy()),win='pred',opts=dict(title = 'pred'))

实例程序：

import  torch
import  torch.nn as nn
import  torch.nn.functional as F
import  torch.optim as optim
from    torchvision import datasets, transforms

from visdom import Visdom

batch_size=200
learning_rate=0.01
epochs=10

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       # transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, transform=transforms.Compose([
        transforms.ToTensor(),
        # transforms.Normalize((0.1307,), (0.3081,))
    ])),
    batch_size=batch_size, shuffle=True)



class MLP(nn.Module):

    def __init__(self):
        super(MLP, self).__init__()

        self.model = nn.Sequential(
            nn.Linear(784, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 200),
            nn.LeakyReLU(inplace=True),
            nn.Linear(200, 10),
            nn.LeakyReLU(inplace=True),
        )

    def forward(self, x):
        x = self.model(x)

        return x

device = torch.device('cuda:0')
net = MLP().to(device)
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
criteon = nn.CrossEntropyLoss().to(device)

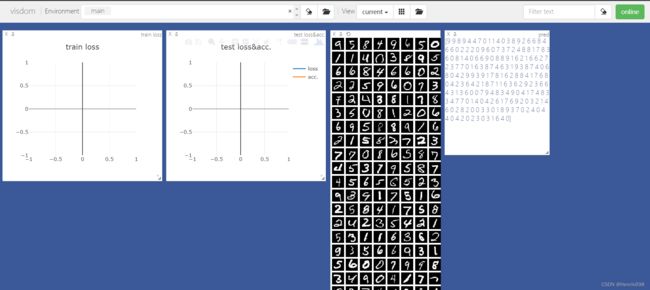
viz = Visdom()

viz.line([0.], [0.], win='train_loss', opts=dict(title='train loss'))
viz.line([[0.0, 0.0]], [0.], win='test', opts=dict(title='test loss&acc.',
                                                   legend=['loss', 'acc.']))
global_step = 0

for epoch in range(epochs):

    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.view(-1, 28*28)
        data, target = data.to(device), target.cuda()

        logits = net(data)
        loss = criteon(logits, target)

        optimizer.zero_grad()
        loss.backward()
        # print(w1.grad.norm(), w2.grad.norm())
        optimizer.step()

        global_step += 1
        viz.line([loss.item()], [global_step], win='train_loss', update='append')

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))


    test_loss = 0
    correct = 0
    for data, target in test_loader:
        data = data.view(-1, 28 * 28)
        data, target = data.to(device), target.cuda()
        logits = net(data)
        test_loss += criteon(logits, target).item()

        pred = logits.argmax(dim=1)
        correct += pred.eq(target).float().sum().item()

    viz.line([[test_loss, correct / len(test_loader.dataset)]],
             [global_step], win='test', update='append')
    viz.images(data.view(-1, 1, 28, 28), win='x')
    viz.text(str(pred.detach().cpu().numpy()), win='pred',
             opts=dict(title='pred'))

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))