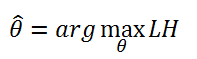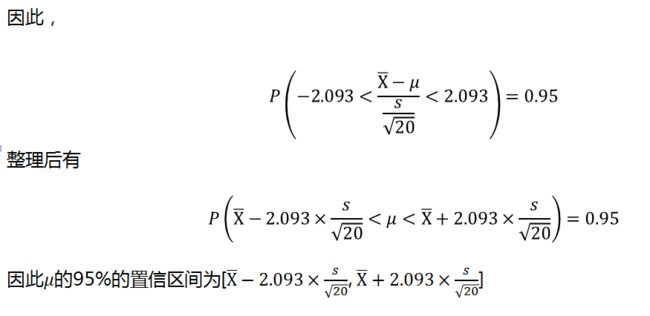金融业信贷风控算法2-初等统计理论
文章目录
- 一. 假设检验
-
- 1.1 什么是假设检验
- 1.2 定义
- 1.3 原假设与备择假设
- 1.4 统计量与显著性水平
- 1.5 单侧检验和双侧检验
- 1.6 常用的假设检验
- 二.参数估计
-
- 2.1 参数估计的方法
- 2.2 矩估计
- 2.3 极大似然估计
- 2.4 两种方法的对比
- 三. 置信区间
-
- 3.1 置信区间概述
- 3.2 置信区间的构造案例
- 四. 线性回归模型
-
- 4.1 线性回归模型
- 4.2 一元线性回归模型
- 4.3 线性回归模型的参数估计
-
- 4.3.1 最小二乘法
- 4.4 极大似然估算法
- 4.5 线性回归中的假设检验
- 五. 案例-性别对违约概率的影响
- 参考:
一. 假设检验
1.1 什么是假设检验
在信贷风控中一个很常见的场景:有一批信贷客户,一部分的受教育年限在12年以上(记为客群A),另一部分在12年以下( 记为客群B)。统计发现,客群A中有5%的人群发生违约,而客群B中有20%的人群发生违约。我们不禁怀疑,受教育年限与信贷违约之间存在某种联系:受教育年限越长则信贷违约概率越小。
由于这个现象只是一部分样本的情形,在全部信贷客群未知的情况下,如何检验论断的可靠性?即上述论断受随机因素影响的可能性有多大?“假设检验”可以帮助我们给出答案。
1.2 定义
假设检验(Hypothesis Testing)是数理统计学中根据一定假设条件由样本推断总体的一种方法。通常会提出一个假设,使得样本的某种统计量在该假设成立时,其分布是已知的(包括分布的类型和参数)。如果该统计量基于已知样本计算出的值,在分布中是“不太可能”发生的,则该假设不成立。这样的假设称之为原假设,通常是简单、易获取的、并且也是不希望成立的。

1.3 原假设与备择假设
在假设检验中,原假设 0 _0 H0需要满足:
- 在 0 _0 H0成立的时候,样本的某个统计量S的分布是已知的
- 0 _0 H0往往是我们想要排除的结论
与原假设互斥的事件则构成了备择假设。
例如,在“受教育年限”与“违约”的例子中,原假设 0 _0 H0就是“受教育年限与违约不相关”。在原假设之下,违约事件是独立同分布的伯努利事件,即每个个体发生违约的概率是一样的。假设客群A和B中分别有100和200个样本,其中有5和40个违约。概率的估计为p=(5+40)/(100+200)=0.15。此时A和B中的违约人群的期望值应当是100×0.15=15, 200×0.15=30, 与实际的人群不符合。不要紧,这样的不符合也许是由于随机因素引起的。那么,这种随机因素究竟能多大程度上引起上述的不符合呢?
1.4 统计量与显著性水平
构造统计量的时候需要遵循的原则是,该统计量在原假设成立的时候其分布是已知的(当然统计量的分布跟样本的分布一般情况下是不同的)。由于样本是总体中随机抽取的一部分,因而也带有随机性。因此需要检验该统计量在服从的分布下的显著性水平。所谓显著性水平,是指统计量等于此观测值甚至更极端的情形下的概率。
例如,对于一个新的信贷产品,前期评估会有5%的客群发生违约。实际放贷后发现一批大小为200人的样本中有50人发生了违约。令原假设 0 _0 H0为“违约率等于5%”,则备择假设 1 _1 H1为“违约率大于5%”。我们构造的统计量是“违约人群”,在原假设成立的情况下违约人群服从二项分布(200, 0.05)。注意到,实际发生违约的人群有50个,大于原假设下的违约人群的期望值。因此我们计算违约人群大于等于50人的“单侧”概率,结果≈0.这样的一个概率通常称为p-值(p-value).
上述例子中,p-值≈0的意义在于,如果原假设是成立的,则违约人群大于等于50人发生的概率非常小,可以认为该事件是不能成立的。
“非常小“是一个很主观的描述,我们需要定量地衡量在原假设成立下,统计量等于观测值(或者更加极端)的概率;也可看成在原假设成立下,我们错误地拒绝原假设的概率。这个概率小到什么程度,需要和一个标准的值来做对比。这样的一个标准的值被称为显著性水平。如果某个原假设的p-值低于显著性水平,则称该原假设是成立的;反之则视为不能拒绝。
注意,显著性水平的选择是不固定的。通常用较小的数值做表示,如0.1,0.05,0.01,0.001等等。如果p值为0.07,当我们用0.1来衡量时,此结果是显著的,即原假设不成立;当我们用0.05来衡量时,此结果又是不显著的,即原假设无法拒绝。
1.5 单侧检验和双侧检验
注意到,上一个例子中原假设是“违约率等于5%”而备择假设是“违约率大于5%”。很显然备择假设中的事件空间只是原假设的事件的补集空间的“一半”,因此称之为单侧检验。在其他场景中,备择假设可以是原假设的事件的补集空间。例如,当原假设是“违约率等于5%”时,备择假设也可以是“违约率不等于5%”,即为双侧检验。单、双侧检验需要依照场景的不同来进行区分。
1.6 常用的假设检验
-
二项检验
一系列伯努利事件中,如果要检验事件发生的概率是否等于某个值,可以用二项检验 -
卡方检验
当检验两类离散因素A与B是否相关时,使用卡方检验。其核心思想是检验理论频数与观测频数之间的差异是否是由随机因素引起的。例如, 检验“性别”是否会影响“违约”时,就可以使用卡方检验 -
z检验
当两组样本的方差已知时,使用z检验来判断两组样本的均值是否相等。例如,违约人群与正常人群的收入的方差已知,当检验两类人群的收入的均值是否相等时,就可以使用z检验 -
t-检验
根据使用场景的不同,t-检验分为单总体和双总体t-检验2中模式。
单总体t-检验:当总体服从正态分布、样本量较少(例如少于30)且方差未知时,检验总体均值是否等于某个已知值。例如,搜集了25名违约人群,在假设其收入服从正态分布时,检验其收入的均值是否等于10K。 -
双总体检验
当两组样本的总体都服从正态分布且方差未知时,检验两组样本所在总体均值是否相等。例如,违约人群与正常人群的收入的方差未知,当检验两类人群的收入的均值是否相等时,就可以使用t检验
二.参数估计
2.1 参数估计的方法
参数估计是从有限样本中推断总体分布的参数的一种方法。例如,搜集了一批信贷客群的收入后,假设收入服从正态分布,则需要推断出正态分布的期望值与方差。
常用的方法有:
- 矩估计
- 极大似然估计
估计量优良评定标准:
- 无偏性:估计量的期望等于被估计的量。样本均值和样本方差分别是总体均值和总体方差的无偏估计
- 有效性:在期望值相等的条件下,考虑方差,方差小的估计量,有效性好
- 一致性:估计量依概率收敛于被估计量(样本均值和方差分别是总体均值和方差的一致估计)
2.2 矩估计
矩估计是基于样本的n阶矩(moment)来估计总体的n阶矩方法。所谓总体的n阶矩,是指随机变量的n次方的期望值。例如,当随机变量服从Font metrics not found for font: .时,总体的一阶和二阶矩是
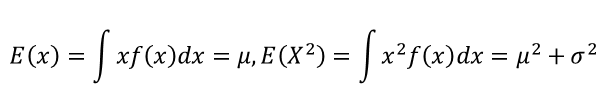
假设分布函数中有k个参数需要估计,则一般情况下可以构造样本与总体的从第1阶矩到第k阶矩,形成方程组进行求解。以正态分布为例:
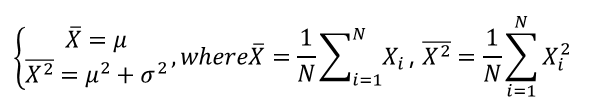
2.3 极大似然估计
与矩估计不同的是,极大似然估计是从样本的分布函数最大化的角度出发进行参数估计。其思想是,利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。如果观测值 1 , 2 , . . , _1,_2,..,_ X1,X2,..,Xn独立同分布于(), 则

对于连续可导的LH,可以通过求解/=0来得到的估计值。
2.4 两种方法的对比
需要注意的是:
- 矩估计法和极大似然估计法给出的参数估计并不是总是一致的。
- 矩估计的优点是简单,只需知道总体的矩,总体的分布形式不必知道。而最大似然估计则必须知道总体分布形式,并且在一般情况下,似然方程组的求解较复杂,往往需要通过数值优化的算法才能计算出其近似解。
三. 置信区间
3.1 置信区间概述
置信区间是另一种表达统计量可能出现的范围的方法。例如,考虑以下情形:假设信贷客群的收入的总体服从正态分布,需要估计收入的期望值。收入的期望值可以用样本均值进行估计,但是由于有随机性的存在,样本均值的大小依赖样本的选取,且估计值的可靠程度也与搜集样本的大小有关。此时我们可以构造置信区间,使得该区间有较大的可能性将真值包含其中。
从名称可以看出,置信区间由2个重要的因素构成:
- 区间范围I
- 置信度%
所谓的置信度,是指通过N次构造I的方法,使得从统计上有N×%的区间I包含了真值。
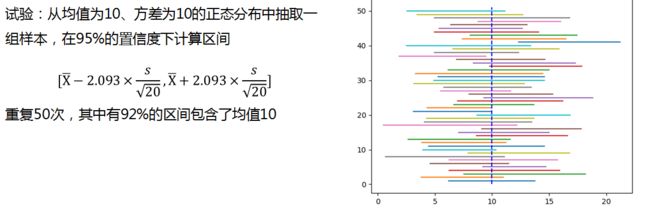
3.2 置信区间的构造案例
四. 线性回归模型
4.1 线性回归模型
在实际工作用,我们不仅需要知道某个随机变量的分布,我们还需要知道某个随机变量(即因变量, dependent variable)与其他已知变量(即自变量,independent variable)的关系(注:在统计模型里,自变量一般不认为是随机变量。但是在计量经济学中,自变量可以看成随机变量)。例如,在信贷风控中,我们关心贷款额度与收入的关系。可以想象,收入高的客群,总体的授信额度会高于收入低的人群。
像这样的,存在因变量与自变量关系的模型称之为监督式模型(supervised model)。特别地,如果因变量是连续型变量,我们称之为回归模型。在回归模型里,结构最简单的是具有以下结构特征的线性回归模型:

4.2 一元线性回归模型
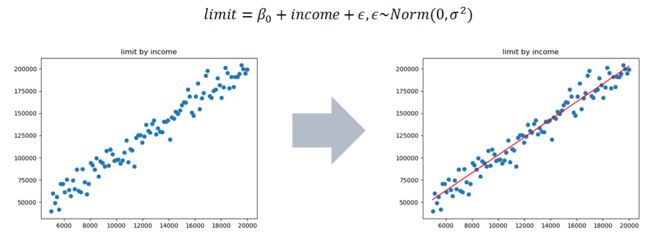
当自变量只有一个因素时,称为一元线性回归模型。例如,我们考虑授信额度与利率的关系:
4.3 线性回归模型的参数估计
从图中可以看出,大的趋势上收入越高、授信额度越高。当我们搜集到若干个样本的授信额度和收入数据后,如何估计出系数参数呢?
在线性回归模型的参数估计中,通常用两种方法进行参数的估计:
- 最小二乘法
- 极大似然估计法
其中,最小二乘法不依赖于噪声的分布。它的原理是给定了损失函数后,寻找最优的系数参数使得损失函数最小化。而极大似然估计法则需要知道噪声的分布,通过最大化(对数)似然函数来寻找最优的系数参数。
4.3.1 最小二乘法
4.4 极大似然估算法
4.5 线性回归中的假设检验
在实际工作中,我们经常遇到一个问题:某自变量对因变量的影响是否是显著的?例如,在建立收入(I,单位为万)与工作年限(W,单位为年)对授信额度(L,单位是十万)的回归模型时,如果建立的模型为
=0.5+0.1×+0.02×
我们关心拟合出来的系数0.1与0.02有多大的概率是受到随机因素的影响。是否有可能在另一批样本中,拟合出来的系数是负或者0?此时可以用假设检验的方式来检验变量的显著性。
原假设:_=0 vs 备择假设:_>0 (或者其他类型,例如_≠0 )
如果我们能有效地拒绝原假设,则可以接受被择假设。

五. 案例-性别对违约概率的影响
参考:
- http://www.dataguru.cn/mycourse.php?mod=intro&lessonid=1701
- https://zhuanlan.zhihu.com/p/86178674