【机器学习】21天挑战赛学习笔记（三）

​

活动地址：CSDN21天学习挑战赛

学习的最大理由是想摆脱平庸，早一天就多一份人生的精彩；迟一天就多一天平庸的困扰。各位小伙伴，如果您：
想系统/深入学习某技术知识点…
一个人摸索学习很难坚持，想组团高效学习…
想写博客但无从下手，急需写作干货注入能量…
热爱写作，愿意让自己成为更好的人...

学习日记

目录

学习日记

1，学习知识点

2，学习的收获

1.CONVEX BICLUSTERING摘要

2.CONVEX BICLUSTERING介绍

3.双聚类的凸形式

---

1，学习知识点

1.CONVEX BICLUSTERING摘要

2.CONVEX BICLUSTERING介绍

3.双聚类的凸形式

2，学习的收获

根据以上的学习知识点进行学习总结，总结知识点如下：

1.CONVEX BICLUSTERING摘要

首先对于 CONVEX BICLUSTERING做一个描述，CONVEX是凸面的，所以我们很容易就知道CONVEX BICLUSTERING是一个凸双聚类。

在双聚群问题中，我们寻求同时对观察结果和特征进行分组，虽然聚簇在从文本挖掘到协同过滤的广泛领域都有应用，但在高维基因组数据中识别结构的问题激发了这项工作。

在这种情况下，双聚簇使我们能够识别仅在实验条件子集内共同表达的基因子集，我们给出了双聚类问题的凸公式（目标函数为凸），它具有唯一的全局最小值和一个保证识别它的迭代算法（COBRA）

---

学习回忆站：

还能记得什么是凸函数吗？

设函数为凸函数，当且仅当对定义域中任意两点和任意实数，总有：

 

通过图像直观来看，凸函数上任意浪点连接而成的虚线，永远在凸函数曲线的上方，如图所示：

---

•  它的简单性、可解释性和算法保证——这些特征可以说是目前替代算法所缺乏的；
• 我们展示了我们的方法的优势，包括在模拟和真实的微阵列数据上稳定和可重复地识别双簇。

2.CONVEX BICLUSTERING介绍

 在双聚类问题中，我们试图同时对数据矩阵中的观察值（列）和特征（行）进行分组。这种数据有时被描述为双向的，或可转换的，以将行和列放在平等的基础上，并强调在行和列变量中揭示结构的愿望。

双聚类用于广泛领域的可视化和探索性分析。

在协同过滤中，它可以用于识别对产品子集有相似偏好的客户子群（霍夫曼和普济查，1999）

在这项工作中，我们专注于双聚簇来识别高维癌症基因组数据的模式

亚型发现可以作为一个双聚类问题提出，其中基因表达数据被划分成一个棋盘状的模式

COBRA输出的结果保留了聚类树图的简单可解释性和可视化，并且与现有技术相比还具有几个关键优势：

• 稳定性和唯一性：COBRA为凸规划产生唯一的全局最小化，该最小化在数据中是连续的。这意味着COBRA总是将数据映射到单个双聚类分配，并且这个解决方法是稳定的。
• 简单性：COBRA采用单个调谐参数（a single tuning paramete）来控制双簇的数量；
• 数据自适应性：COBRA允许一个简单而有原则的数据自适应过程，用于选择涉及凸矩阵完成问题的调整参数。

3.双聚类的凸形式

双聚类的算法

---

1.算法简介

       双聚类简单来说就是在数据矩阵A中寻找一个满足条件矩阵B1的子矩阵A1，而B1是条件矩阵B的一个子矩阵.

2.算法常用的计算模型

       目前定义双聚类算法有四种比较广泛的方式：(括号中为sklearn官网的说法)

2.1等值模型(常数值，常量行或常量列)

2.2加法模型(低方差的子矩阵) 

2.3乘法模型(异常高或低的值) 

2.4信息共演模型(相关的行或列) 

3.两种特殊的双聚类结果(sklearn官网有算法的) 

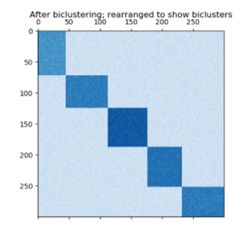
3.1对角线结构

 

3.2棋盘格结构

 

4.双聚类的两种算法

        双聚类的算法有很多种，这里只介绍sklearn官网提供的两种算法，也就是上述两种特殊结构的算法。

4.1光谱联合聚类(Spectral Co-Clustering)

        说明：因为我们不自己动手写算法，所以这里的公式就略过了。

4.1.1 算法作用

       该算法找到的值高于相应的其他行和列中的值。每行和每列只属于一个双聚类，因此重新排列行和列中的这些高值，使这些分区沿着对角线连续显示。

4.1.1 主要计算过程

      1)按照数学公式对矩阵进行预处理

      2)对处理后的矩阵进行行和列的划分，之后按照另外一个数学公式生产一个新的矩阵Z

      3)对矩阵Z的每行使用k-means算法

4.1.2 sklearn中的函数

     1) sklearn.cluster.bicluster. SpectralCoclustering

     2)主要参数(详细参数)

       n_clusters ：聚类中心的数目，默认是3

       svd_method：计算singular vectors的算法，‘randomized’(默认) 或 ‘arpack’.

       n_svd_vecs ：计算singular vectors值时使用的向量数目

       n_jobs ：计算时采用的线程或进程数量

  3)主要属性

       rows_ :二维数组，表示聚类的结果。其中的值都是True或False。如果rows_[i,r]为True，表示聚类i包含行r

      columns_:二维数组，表示聚类的结果。

      row_labels_ ：每行的聚类标签列表

      column_labels_ :每列的聚类标签列表

4.2光谱双聚类(Spectral Biclustering)

4.2.1 算法作用

      该算法假定输入的数据矩阵具有隐藏的棋盘结构，因此可以对其中的行和列进行划分，使得行簇和列簇的笛卡尔积中的任何双聚类的条目近似恒定。例如，如果有两个行分区和三个列分区，则每行将属于三个双聚集，而每列将属于两个双聚集。

      该算法对矩阵的行和列进行划分，使相应的blockwise-constant棋盘格矩阵能够很好地逼近原始矩阵。

4.2.2 主要计算过程

     1)对矩阵进行归一化

     2)计算前几个singular vectors 值(奇异向量？总感觉这么翻译很别扭)

     3)根据这些singular vectors值进行排序，使其可以更好的通过piecewise-constant向量进行近似表示

    4) 使用一维k均值找到每个向量的近似值，并使用欧几里德距离进行评分

    5) 选择最佳左右singular vectors的一些子集

    6) 将数据投影到这个singular vectors的最佳子集并聚集

4.2.3 sklearn中的函数

     1) sklearn.cluster.bicluster.SpectralBiclustering

     2)主要参数(详细参数)

       n_clusters ：单个数值或元组，棋盘结构中的行和列聚集的数量

       method：把singular vectors值归一化并转换成biclusters的方法。默认值是‘bistochastic’。

    3)主要属性

       rows_ :二维数组，表示聚类的结果。其中的值都是True或False。如果rows_[i,r]为True，表示聚类i包含行r

      columns_:二维数组，表示聚类的结果。

      row_labels_ ：每行的分区标签列表

      column_labels_ :每列的分区标签列表

这一部分为网上数据资料，仅供参考~~

---

 对于权重的明智选择我们能够：

• 使用单个正则化参数；
• 获得更简洁的聚类；
• 加速CORBA使用的关键字程序的收敛。