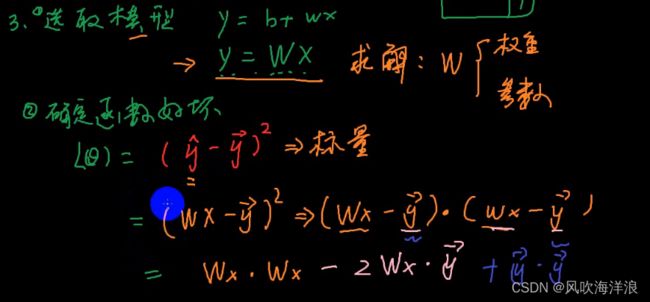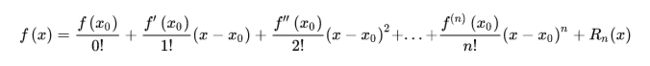机器学习【基于sklearn库】-回归、分类、聚类
机器学习-回归、分类、聚类
- 1.是什么?
- 2.一些基础概念(建议先看具体例子再返过来看概念)
-
- mse均方误差、r2等等衡量标准
- 过拟合和欠拟合
-
- 为了防止过拟合方法:
-
- 正则化L1、L2(优化最小二乘法损失函数/代价函数)
- 方差var和偏差bias
- 特征缩放和交叉验证
-
- 特征缩放方法
-
- 数据归一化
- 均值标准化
- 交叉验证
- 3.按照标签的多少和有无来分类:
-
- 3.1.监督学习
-
- 回归
-
- 一次方线性回归原理
-
- 损失函数/代价函数(衡量model内部函数哪个更好的方法)
- (1)计算模型中函数的方法:
-
- 标准方程法(矩阵可逆时)-原理线代投影/(正规方程组求解最小二乘法)(根据损失函数可以直接计算出来)
- 衡量拟合程度方法:相关系数/决定系数r2(跨model衡量拟合程度)
- 多项式(多次方)线性回归(基于泰勒近似和一次方线性回归)
- (2)计算模型中函数的方法-梯度下降法(求解最小二乘法的方法)(不可逆矩阵无法直接计算)
-
- 自适应学习率
- 岭回归(:L2正则化损失函数用于线性回归)
- LASSO回归(L1正则化用于线性回归)
- 弹性网ElasticNet(正则化L1、L2公式结合)
-
- sklearn实现弹性网(正则化L1、L2公式结合)
- 线性和非线性回归实践
-
- 实践1:生成数据集然后拟合曲线(正规方程式求解最小二乘法方法和sklearn库)
- 实践2:sklearn波士顿房价(LassoCV套索回归)
- 实践3:sklearn实现 多项式回归(也是用sklrean线性回归模型)
- 实践4:使用梯度下降方法实现线性回归
- 实践5:sklearn实现 岭回归
- 实践5:sklearn实现 lasso回归
- 分类
-
- 逻辑回归(基于线性回归)
-
- 损失函数/代价函数
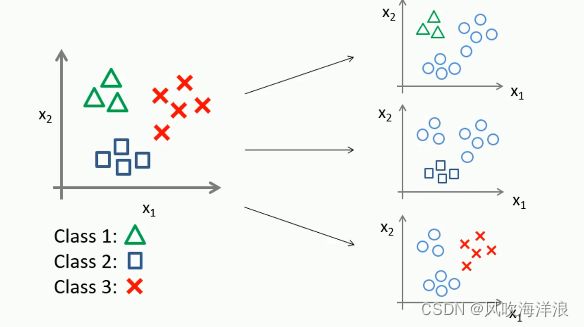
- 二分类扩展到多分类
- 一些基础概念(正确率和召回率、F1指标)
- 线性和非线性分类实践
-
- sklearn实现线性逻辑回归
- sklearn实现非线性逻辑回归
- 3.无监督学习
-
- 聚类
1.是什么?
机器学习:人工智能实现一种方法。机器学习属于人工智能的一个分支。
机器学习就是用算法解析数据,不断学习,对世界中发生的在这里插入代码片事做出判断和预测的一项技术。
人工智能是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门技术科学。
机器学习就是自学习找到一定的满足功能的函数f(x),x为输入,用矩阵来表示
矩阵的组成表很多列为特征,其中一列为标签。
根据标签的多少和有无分为:(根据与数据交互方式:)
监督学习
半监督学习
无监督学习
2.一些基础概念(建议先看具体例子再返过来看概念)
mse均方误差、r2等等衡量标准
参考链接:
https://blog.csdn.net/u012735708/article/details/84337262
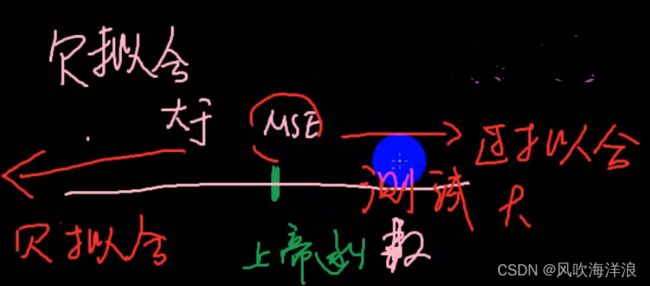
过拟合和欠拟合
欠拟合:可以无限逼近拟合真实的函数(但谁都不知道这个函数真实是什么样子的,即上帝函数),在达到之前衡量指标mse一直是大于真实函数的真实mse的
过拟合:训练集数据可以mse很小,但是测试集数据得出的mse很大
为了防止过拟合方法:
过拟合一般都是一个简单的问题用了很复杂的模型
减少特征:就是为了简化模型
增加数据量:数据量多后,训练的不会太复杂,过拟合不会太明显
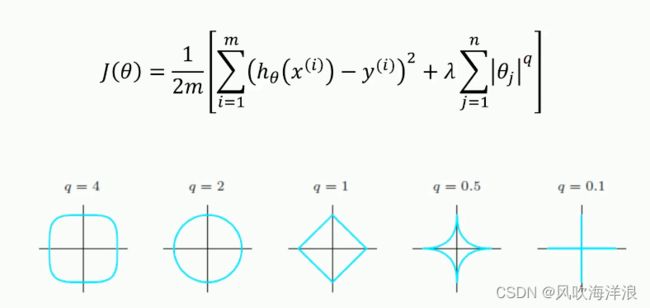
正则化L1、L2(优化最小二乘法损失函数/代价函数)
为了防止过拟合,所以使用正则化,使用了正则化推导出来的计算模型函数参数的公式可以防止特征矩阵不可逆而不能计算。
为什么加了这一项,就可以防止过拟合,加了这一项可以使得模型函数中参数变小,那么拟合的曲线变化慢,越平滑,那么拟合就越好
为什么加了这一项就可以使得模型函数中参数变小:
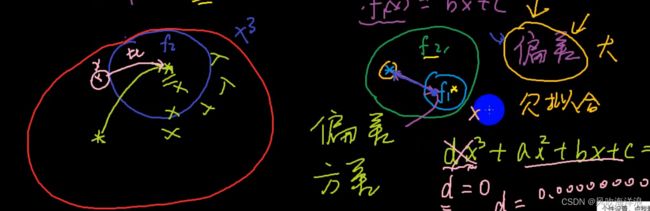
方差var和偏差bias
mse衡量指标有出入的原因:方差和偏差
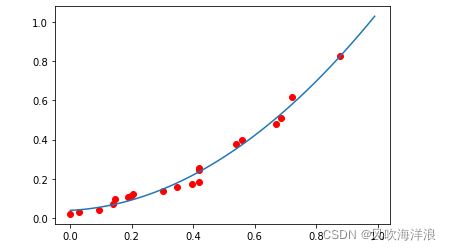
方差:例如一个二次方的函数,用三次方模型无法拟合的很好,mse可能会很小,但方差很大,导致过拟合
因为例如下面案例有个二次方的上帝函数,但是用八次方去拟合这个上帝函数的时候,虽然一开始非常的mse很小,x很小的时候几次方看不出来差距,但当x增大时,次方的差距越来越大,导致方差很大。
偏差:例如一个二次方的函数,用一次方模型无法拟合的很好,导致mse很大,那么导致欠拟合
特征缩放和交叉验证
特征缩放方法
数据归一化
均值标准化
交叉验证
3.按照标签的多少和有无来分类:
3.1.监督学习
监督学习分为:回归、分类
回归
一次方线性回归原理
参考链接:
//从原理讲回归:
https://www.bilibili.com/video/BV1Rt411q7WJ?p=5
//从向量讲回归,
https://www.bilibili.com/video/BV1cJ411V7K2?p=8&spm_id_from=pageDriver
//其中涉及的为什么能够去回归和拟合一个模型去求解,参考线代的投影:
https://zhuanlan.zhihu.com/p/157490048?from_voters_page=true
回归分析:用来建立方式来模拟两个或者多个变量之间是如何关联的
1.回归输出是一个连续型的向量
2.找到一个模型(一些函数的集合)
例如:y=b+wx 一元线性回归(数据里有一个特征) 其中代表了很多具体的函数
3.如何在模型里确定哪个函数更好,更贴合场景和情况。
例如:关于某小区的房价预测,在数据集中训练模型(一些函数集合),然后根据现有某小区的数据预测出贴合该小区的房价(具体的函数),用函数线来拟合现有的数据点
损失函数/代价函数(衡量model内部函数哪个更好的方法)
4.【代价函数/损失函数】如何判断那么多具体函数哪个是最好的,衡量方法
(1)计算模型中函数的方法:
标准方程法(矩阵可逆时)-原理线代投影/(正规方程组求解最小二乘法)(根据损失函数可以直接计算出来)
标准方程方法:原理就是根据最小二乘法推出来的公式。(只有特征矩阵可逆的时候才可以直接计算)

5.已经知道改变下面公式的两个变量会影响这条回归线走向,会影响计算出来的损失函数的值,为了让损失函数值最小,有什么方法来算出来呢?
如何求解模型中最贴合当前数据的函数(或者一元一次方程)
方法1:线代投影
//从向量讲回归:
https://www.bilibili.com/video/BV1cJ411V7K2?p=8&spm_id_from=pageDriver
//其中涉及的为什么能够去回归和拟合一个模型去求解,参考线代的投影:
https://zhuanlan.zhihu.com/p/157490048?from_voters_page=true
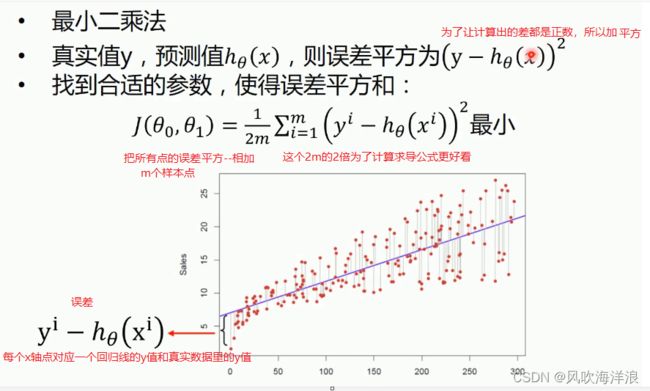
方法2:最小二乘法求导
例如线性回归里面用的最小二乘法:值越小越好
参考链接:
https://www.bilibili.com/video/BV1cJ411V7K2?p=17&spm_id_from=pageDriver
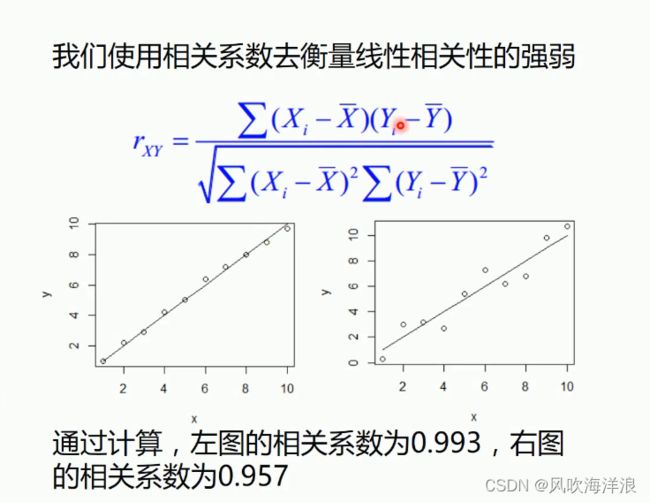
衡量拟合程度方法:相关系数/决定系数r2(跨model衡量拟合程度)
除了损失函数,还有两种方式来衡量拟合程度
1.相关系数(线性、两个变量)
相关系数绝对值越接近1,采样点的分布越接近线性关系
相关系数越接近1,表示样本点的分布越接近正相关关系
相关系数越接近-1,表示采样点分布越接近负相关关系
相关系数越接近0,表示样本点分布呈不接近线性关系
2.决定系数(非线性、两个及以上变量)
()样本点真值、y拔)样本点真值平均值、y尖)预测值
系数r越接近1,表示自变量之间越接近线性关系,用于测量线性模型的结果。
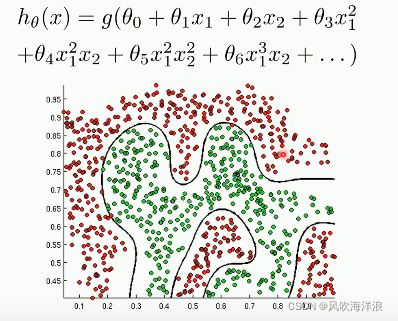
多项式(多次方)线性回归(基于泰勒近似和一次方线性回归)
参考链接:
https://www.bilibili.com/video/BV1cJ411V7K2?p=18
泰勒近似原理:泰勒公式可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数
如何实现拟合,原理就是利用一次方的线性回归模型:将多次方项分别看做新的一个个的特征列,然后带入到一次方的线性回归模型进行计算:
from sklearn.datasets import load_boston
from sklearn import metrics
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#线性回归
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
#我们用随机的数据来模拟出一个二次方的方程的函数样子
np.random.seed(1)
#随机出来是平均分布
X=np.random.uniform(0,1,(20,1))
y=X**2+np.random.uniform(0,0.1,(20,1))
X=np.sort(X,axis=0)
y=np.sort(y,axis=0)
plt.plot(X,y,"ro")
plt.show()
model=LinearRegression()
model.fit(X,y)
#这个是评估这个模型,采用r2来衡量
model.score(X,y)
#用一些x轴的点,然后用训练好的模型去预测这些点的y值label值,然后画出拟合线
x_=np.arange(0,1,0.01).reshape(-1,1)
y_pre=model.predict(x_)
plt.scatter(X,y)
plt.plot(x_,y_pre,"red")
plt.show()
#二次方拟合
x_1=np.array([X,X**2]).T.reshape(-1,2)
model_1=LinearRegression()
model_1.fit(x_1,y)
model_1.score(x_1,y)
#八次方拟合
x_3=np.array([X,X**2,X**3,X**4,X**5,X**6,X**7,X**8]).T.reshape(-1,8)
model_2=LinearRegression()
model_2.fit(x_3,y)
model_2.score(x_3,y)
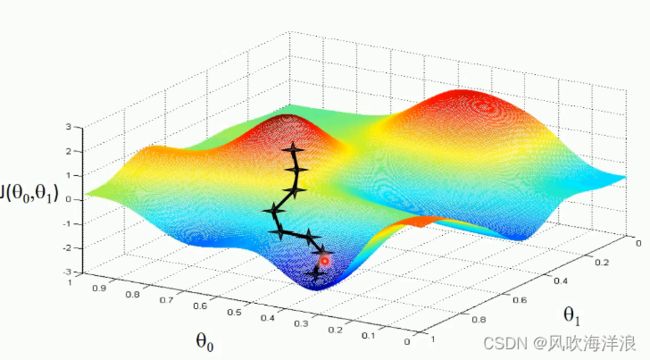
(2)计算模型中函数的方法-梯度下降法(求解最小二乘法的方法)(不可逆矩阵无法直接计算)
损失函数求偏导,为了找到函数下降的最快方向,上升最快方向的反方向。调节学习速率,然后调整步长,有可能陷入局部最小值
梯度:就是使得函数在某一点朝着增长最快的方向,也就是这一点的曲线的切线垂直方向就是最增长最快方向,那么反方向就是下降最快的方向
一个函数求偏导之后,无论在哪一点都会朝着该点所在曲线的垂直方向进行移动。
例如可以利用梯度下降法来优化线性回归中最小二乘法的损失函数:
一次方多元也可以用梯度下降方法:
一个特征,模型为y=kx+b 其中 k,b有两个参数
那么两个特征,模型为y=wx1+rx2+b 三个参数
其中的问题:
如何设置梯度下降迭代什么时候停止?三种方法:自己设定迭代次数、设定损失函数两次计算之间小于一定的值,说明迭代计算的损失函数下降的慢了,可能达到了最小值、其他(自适应学习率)
自适应学习率
其中的问题:
如何设置梯度下降迭代什么时候停止?
三种方法:
1.自己设定迭代次数、
2.设定损失函数两次计算之间小于一定的值,说明迭代计算的损失函数下降的慢了,可能达到了最小值、
3.其他(自适应学习率)
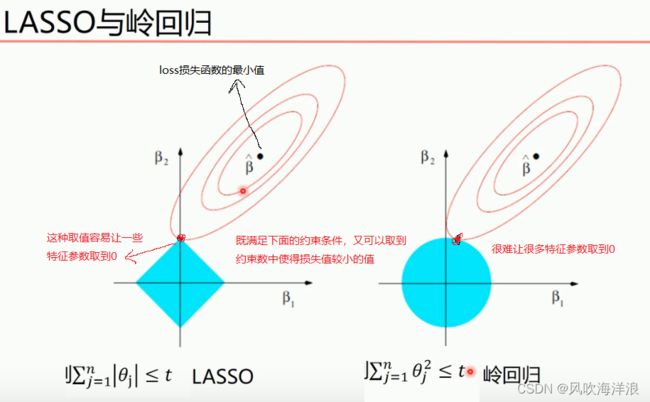
岭回归(:L2正则化损失函数用于线性回归)
特征矩阵不可逆的时候无法通过最小二乘法来进行直接计算出模型函数。
岭回归使用了正则化的L2方法
LASSO回归(L1正则化用于线性回归)
区分一下岭回归和lasso回归
弹性网ElasticNet(正则化L1、L2公式结合)
正则化L1、L2可以有很多种变形
综上提出了弹性网:(结合了l1、l2)
sklearn实现弹性网(正则化L1、L2公式结合)
sklearn.linear_model.ElasticNetCV()
线性和非线性回归实践
实践1:生成数据集然后拟合曲线(正规方程式求解最小二乘法方法和sklearn库)
使用jupyter实现代码,生成一些数据,然后分为训练和测试数据,然后用两种方式训练处模型,一种是底层原理线代投影计算出模型,一种是利用sklearn机器学习算法库进行计算出
```python
# 引入机器学习库,然后测试和训练分离
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn import metrics
import matplotlib.pyplot as plt
import numpy as np
import time
%matplotlib inline
X,y=datasets.make_regression(n_samples=250,n_features=1,noise=10,random_state=0,bias=50)
#将生成的数据分为两份:训练一部分,测试用一部分
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
o_train=np.ones([X_train.shape[0],1],dtype=X_train.dtype)
o_test=np.ones([X_test.shape[0],1],dtype=X_test.dtype)
print(X.shape)
print(o_train.shape)
print (o_test.shape)
X_train =np.concatenate((o_train,X_train),axis=1)
X_test =np.concatenate((o_test,X_test),axis=1)
plt.scatter(X, y)
!!!!!对于生成的这些数据集采用两种方式来进行训练模型,生成预测值
1.利用原理自己实现一元线性回归模型预测
# 这个就是A矩阵(用数据集里的数据特征组成的)
X_train[:5]
array([[ 1. , -0.66347829],
[ 1. , -0.4664191 ],
[ 1. , -1.00021535],
[ 1. , 2.25930895],
[ 1. , -0.67433266]])
#theta =(ATA)逆矩阵 AT y
theta=np.dot(np.dot(np.linalg.inv(np.dot(X_train.T,X_train)),X_train.T),y_train)
theta
#上面计算(训练)得出来的两个值分别是 y=wx+b 的w和b
#那么可以通过两点画出一条直线
x_0=np.min(X)
y_0=x_0*theta[1]+theta[0]
x_1=np.max(X)
y_1=x_1*theta[1]+theta[0]
plt.scatter(X, y)
plt.plot([x_0,y_0],[x_1,y_1],c='r')
2.利用sklearn机器学习库进行调包实现
# 导入线性模型
from sklearn import linear_model
from sklearn import metrics
model=linear_model.LinearRegression()
#用训练数据进行训练模型
model.fit(X_train,y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
#用训练好的模型进行用测试数据进行预测
pr_result=model.predict(X_test)
print(pr_result)
#对比一下预测的数据与真实的数据
print(y_test)
[68.06337532 32.55513372 38.32076468 61.18826024 36.30490259 41.32963489
46.44191426 46.13682263 42.25612589 33.00436662 89.66861421 50.01369359
[63.91415379 27.38377446 31.47248549 66.94964684 46.29572542 42.65361897
47.12842033 25.59512398 38.24928203 24.39842909 98.9891604 52.39146356
#计算一下损失函数最小二乘法:最小越好
mse=metrics.mean_squared_error(y_test,pr_result)
print(mse)
#计算一下R2的值:决定系数(非线性、两个及以上变量)
#()样本点真值、y拔)样本点真值平均值、y尖)预测值
#系数r越接近1,表示自变量之间越接近线性关系,用于测量线性模型的结果。
r2=metrics.r2_score(y_test,pr_result)
print(r2)
88.57374740272209
0.8103354083629025
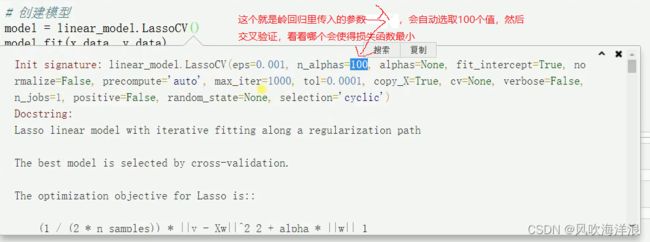
实践2:sklearn波士顿房价(LassoCV套索回归)
学习参考链接:
https://www.bilibili.com/video/BV1mK411N7pP/
sklearn是什么:?就是基于python的机器学习算法库
参考链接:
https://blog.csdn.net/gxc19971128/article/details/106467024/
from sklearn.datasets import load_boston
from sklearn import metrics
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV
import seaborn as sns
#直接调用这个sklearn里面的数据集
shuju=load_boston()
print(shuju.DESCR)
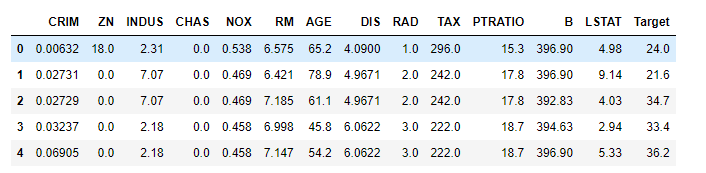
#将数据集里面的列分为特征和目标(标签)
x=shuju.data
y=shuju.target
#将他们放在表格里,表格的列就用数据集里面的特征名字就行
df=pd.DataFrame(x,columns=shuju.feature_names)
df['Target']=pd.DataFrame(y,columns=['Traget'])
df.head()
#画出热力图,可以查看target和各个特征之间的相关性
plt.figure(figsize=(15,15))
p=sns.heatmap(df.corr(),annot=True,square=True)
#数据标准化就是 用数据 减去 这个特征的数据平均值 除以 特征的方差 ,为了让所有数据都是在0附近的数,尺度会好一些
from sklearn.preprocessing import StandardScaler
ss=StandardScaler()
x=ss.fit_transform(x)
# 对数据进行切分,然后分为测试集 训练集
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3)
#这个地方是为了解决一个报错,莫名其妙的报错,有错也不影响这个的实现,但是还是屏蔽一下
import warnings
warnings.filterwarnings("ignore", category=FutureWarning, module="sklearn", lineno=1978)
#使用lasso回归模型 套索回归模型
model=LassoCV()
model.fit(x_train,y_train)
print(model.alpha_)
print(model.coef_)
print(model.intercept_)
#score查看拟合好不好 用的是x用于测试的真实值和y用于测试的真实值
model.score(x_test,y_test)
#metices包里的r2,是用的y的预测值和y的真实值计算
#系数r越接近1,表示自变量之间越接近线性关系,用于测量线性模型的结果。
r2=metrics.r2_score(y_test,pr_result)
实践3:sklearn实现 多项式回归(也是用sklrean线性回归模型)
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
data=np.genfromtxt("job.csv",delimiter=",")
x=data[1:,1]
y=data[1:,2]
plt.plot(x,y,"b.")
plt.show()
#如果直接调用线性模型来进行训练,得到的拟合的线是线性的,拟合效果不好
x_one=data[1:,1,np.newaxis]
y_one=data[1:,2,np.newaxis]
model1=LinearRegression()
model1.fit(x_one,y_one)
plt.plot(x,y,"b.")
plt.plot(x_one,model1.predict(x_one),"r")
plt.show()
#使用多项式回归,其实也是用的线性模型,只不过对特征列进行了处理
poly_reg=PolynomialFeatures(degree=2)
#需要传入一个二维的变量
x_poly=poly_reg.fit_transform(x_one)
model2=LinearRegression()
model2.fit(x_poly,y_one)
plt.plot(x,y,"b.")
plt.plot(x,model2.predict(x_poly))
plt.show()
实践4:使用梯度下降方法实现线性回归
参考链接:
https://www.bilibili.com/video/BV1Rt411q7WJ?p=7
import numpy as np
import matplotlib.pyplot as plt
#获取数据集中的数据两列数据x为特征,y为标签
data=np.genfromtxt("data.csv",delimiter=",")
x=data[:,0]
y=data[:,1]
plt.scatter(x,y)
plt.show()
![]()
#定义一个学习速率lr
lr=0.0001
#设置一元一次函数的参数初始值,b,k
b=0
k=0
#设置梯度下降优化方法的迭代次数
epochs=50
for i in range(epochs):
b_diedai=0
k_diedai=0
m=float(len(x))
for j in range(0,len(x)):
y_prec=k*x[j]+b
b_diedai+=(1/m)*(y_prec-y[j])
k_diedai+=(1/m)*x[j]*(y_prec-y[j])
b=b-lr*b_diedai
k=k-lr*k_diedai
print(b,k)
plt.plot(x,y,'b.')
plt.plot(x,k*x+b,'r')
plt.show()
实践5:sklearn实现 岭回归
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
print(data)
#展示数据,并进行切分
# 切分数据,分为特征列和标签列
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)
# 创建模型
# 生成50个值,因为岭回归里面需要定义参数lambta的值,那么就随机生成一些,然后根据loss损失函数情况来计算出最好的值
alphas_to_test = np.linspace(0.001, 1)
# 创建模型,保存误差值,CV就是使用交叉验证,store_cv_values就是保存一下过程值,就是分为16份
model = linear_model.RidgeCV(alphas=alphas_to_test, store_cv_values=True)
model.fit(x_data, y_data)
# 岭系数
print(model.alpha_)
# loss值
print(model.cv_values_.shape)
#利用训练好的模型预测一下:
model.predict(x_data[2,np.newaxis])
![]()
# 画图
# 岭系数跟loss值的关系
plt.plot(alphas_to_test, model.cv_values_.mean(axis=0))
# 选取的岭系数值的位置
plt.plot(model.alpha_, min(model.cv_values_.mean(axis=0)),'ro')
plt.show()
实践5:sklearn实现 lasso回归
import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
# 读入数据
data = genfromtxt(r"longley.csv",delimiter=',')
# 切分数据
x_data = data[1:,2:]
y_data = data[1:,1]
print(x_data)
print(y_data)
# 创建模型
model = linear_model.LassoCV()
model.fit(x_data, y_data)
import warnings
warnings.filterwarnings("ignore", category=FutureWarning, module="sklearn", lineno=1978)
#lasso参数
print(model.alpha_)
# 相关系数特征的一些参数
print(model.coef_)
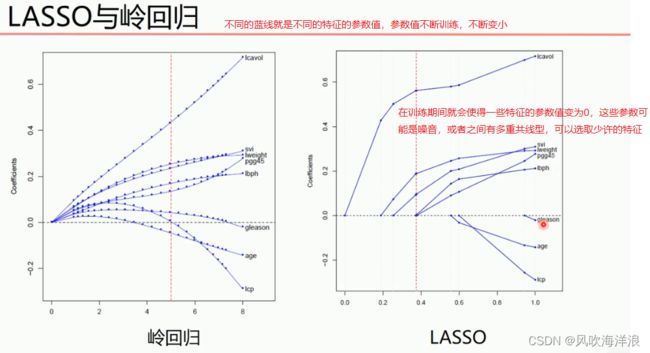
注释:这里可以验证,lasso方法确实会使得一些特征的参数在训练过程中直接为0。可能这几个特征之间有多重共线性,或者对预测列没有太大关系
sklearn的lasso方法,不用向岭回归一样传入alphas的值,自己会传入一些自动选的值
分类
逻辑回归(基于线性回归)
定义逻辑回归的预测函数:
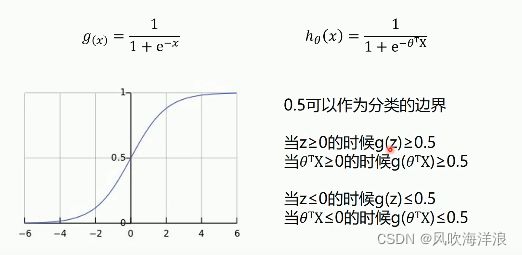
原理:基于线性回归的,将线性函数的结果映射到sigmoid函数中做分类
分类就是分为两个:借助g(x)这个函数
决策边界:就是h(x)=g(θTx)中的θTx函数,两个类别之间的边界:
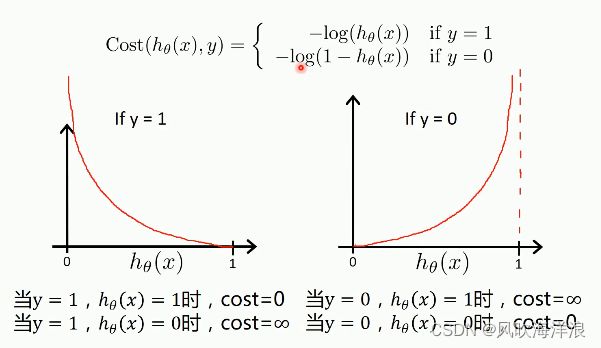
损失函数/代价函数
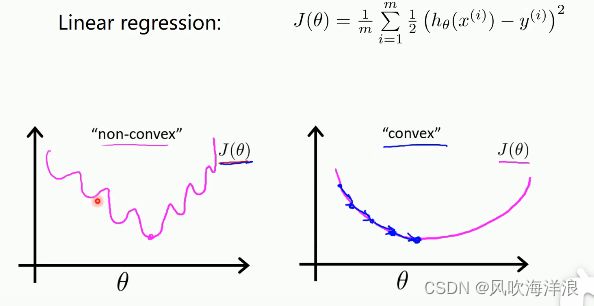
线性回归:代价函数形成的图形是凸函数,使用梯度下降法可以找到最小值,
但分类中逻辑回归,再使用线性回归的代价函数形成是非凸函数,梯度下降法会陷入局部最小值
所以需要换个代价函数
求解方法:
二分类扩展到多分类
一些基础概念(正确率和召回率、F1指标)
线性和非线性分类实践
sklearn实现线性逻辑回归
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing
from sklearn import linear_model
# 载入数据,准备 数据分为0,1进行储存
data = np.genfromtxt("LR-testSet.csv", delimiter=",")
x_data = data[:,:-1]
y_data = data[:,-1]
def plot():
x0 = []
x1 = []
y0 = []
y1 = []
# 切分不同类别的数据
for i in range(len(x_data)):
if y_data[i]==0:
x0.append(x_data[i,0])
y0.append(x_data[i,1])
else:
x1.append(x_data[i,0])
y1.append(x_data[i,1])
# 画图
scatter0 = plt.scatter(x0, y0, c='b', marker='o')
scatter1 = plt.scatter(x1, y1, c='r', marker='x')
#画图例
plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
plot()
plt.show()
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
# 画图决策边界:就是使得代价函数为0的等式,横坐标为x_test,纵坐标为y_test,
plot()
x_test = np.array([[-4],[3]])
y_test = (-logistic.intercept_ - x_test*logistic.coef_[0][0])/logistic.coef_[0][1]
plt.plot(x_test, y_test, 'k')
plt.show()
predictions = logistic.predict(x_data)
print(classification_report(y_data, predictions))
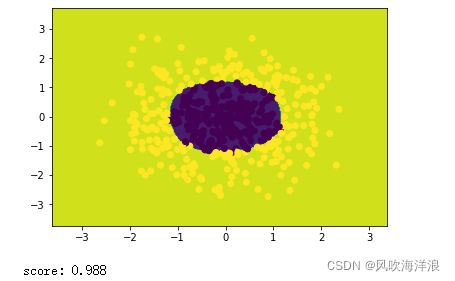
sklearn实现非线性逻辑回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.datasets import make_gaussian_quantiles
from sklearn.preprocessing import PolynomialFeatures
# 生成2维正态分布,生成的数据按分位数分为两类,500个样本,2个样本特征
# 可以生成两类或多类数据
x_data, y_data = make_gaussian_quantiles(n_samples=500, n_features=2,n_classes=2)
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
logistic = linear_model.LogisticRegression()
logistic.fit(x_data, y_data)
# 定义多项式回归,degree的值可以调节多项式的特征
poly_reg = PolynomialFeatures(degree=5)
# 特征处理
x_poly = poly_reg.fit_transform(x_data)
# 定义逻辑回归模型
logistic = linear_model.LogisticRegression()
# 训练模型
logistic.fit(x_poly, y_data)
# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1
# 生成网格矩阵
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
z = logistic.predict(poly_reg.fit_transform(np.c_[xx.ravel(), yy.ravel()]))# ravel与flatten类似,多维数据转一维。flatten不会改变原始数据,ravel会改变原始数据
z = z.reshape(xx.shape)
# 等高线图
cs = plt.contourf(xx, yy, z)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
plt.show()
print('score:',logistic.score(x_poly,y_data))
3.无监督学习
无监督学习分为:聚类