机器学习基础篇(十)——聚类
机器学习基础篇(十)——聚类
一、概论
在前几节(5-9)知识中我们学习的是有关于监督学习的算法,本节开始我们将要开始学习无监督学习的相关知识。
在一个典型的监督学习中,我们有一个有标签的训练集。我们的目标是找到能够区分正样本和负样本的决策边界。
与此不同的是,在无监督学习中,我们的数据没有附带任何标签。我们会通过分析大量的无标签数据,来发现数据内在的一些结构特征。
今天我们将讲解无监督学习的常见算法——聚类。
二、聚类
如图所示,是一个典型的无监督学习样本的相关数据,数据集中没有标签存在。
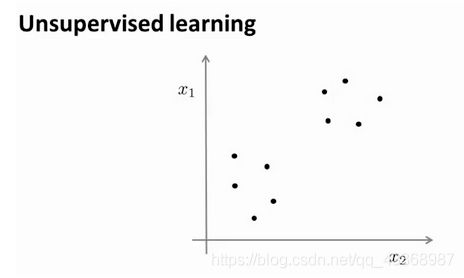
显然我们可以将图示数据分成两类,将相似的对象归为同一类,不相似的对象则划分到不同类中。而我们将数据分成的这两类,称为簇。
用术语来说,就是:
- 聚类是按照某个特定标准(如距离准则)把一个数据集分割成不同的簇。使得同一个簇内的数据对象的相似性尽可能大。
- 同时不在同一个簇中的数据对象的差异性也尽可能地大,即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
- 这听起来和分类很像,但聚类和分类是两个完全不同的概念。
-
聚类并不关心数据集的标签是什么,它的目标只是将相似的数据聚到一起,成为一个类。 -
分类则需要对现有的数据集以及所属标签进行学习,然后对未知数据进行预测,确认其所属分类。
聚类是解决无监督学习常见问题的最有用的技术。我们可以通过对相似的数据点进行分组,来找到数据中的特征。
举个栗子:
- 假如你是一家玩具生产商,你会生产出许多玩具,但是每个玩具所适用的人群不同。
- 所以如何识别出某玩具所对应的特定群体,并且进行精准化广告投放,是十分重要的。
精准的识别出会购买产品的人群,并且对其进行定制化广告营销,这是聚类的作用之一。当我们想要识别原始数据中所潜在的分组,聚类是一种很好用的手段。
三、聚类的方法
既然聚类如此重要,那么我们该如何进行聚类呢?
- 我们可能会考虑数据点之间的距离,并用距离来划分。
- 又或许我们会考虑不同区域中数据点的密集程度,并因此划分不同的簇。
今天我们讲解以下两个方法:K-Means聚类,Hierarchical聚类。
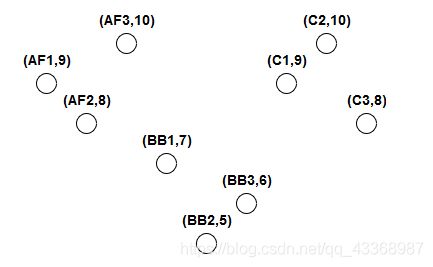
- 首先我们需要一个数据集,以玩具制造商的数据集为例:玩具制造商向5至10岁的幼儿销售3种产品,每种产品有3种。这些产品是动作人物,积木和汽车。
- 制造商还注意到哪个年龄组购买了每种产品的大部分。
- 数据集中的每个点代表玩具和购买其中大部分的年龄组之一。
1.K-Means算法
K-Means算法会使用迭代过程,将数据集划分成K个簇。
- 首先,我们为这K个簇分别选定K个中心点(中心点不一定在数据集中存在,可以是虚拟的点)。
- 中心点有很多种选择方法,比如 {‘k-means++’, ‘random’ or an ndarray}。
- 在下面的示例代码中,我们使用k-means++的方法,这样可以加速中心点的收敛,加快迭代过程。
(关于中心的的选择,此处不再赘述,有兴趣的同学可以参考该链接) - 第二步,我们将每个数据点都分到这K个簇中去。我们通过测量数据点和每个中心点之间的距离,选择中心点最接近的那个簇,作为该数据点的所属分类。
如图所示:
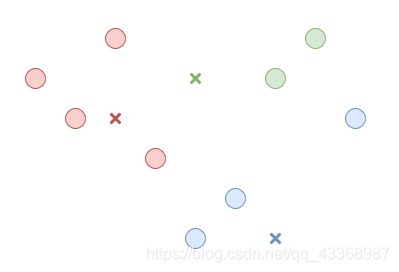
- 第三步,我们重新计算这K簇数据集分别的中心点。每簇的中心点就是这簇所有数据的均值。
如图所示: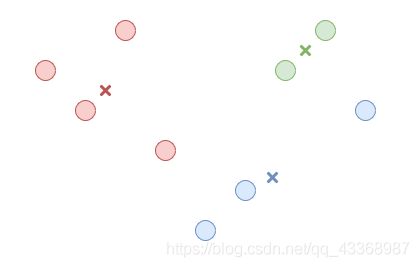
- 重复第二步和第三步,直到中心点不再变化(或者仅在迭代之间微小变动)。此时数据被分成了K类,每类中的数据和该类的中心都是最小的。(相比于该类数据与其他类中心的距离)
如图所示:
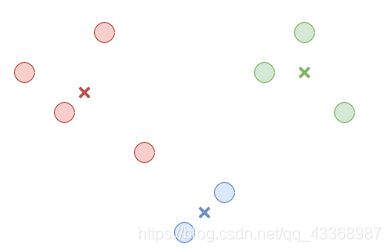
- K-Means算法需要我们预先给定分类的种类数,也就是K的值。
- K的值并不好确定,不同的K值,分类结果自然不一样。
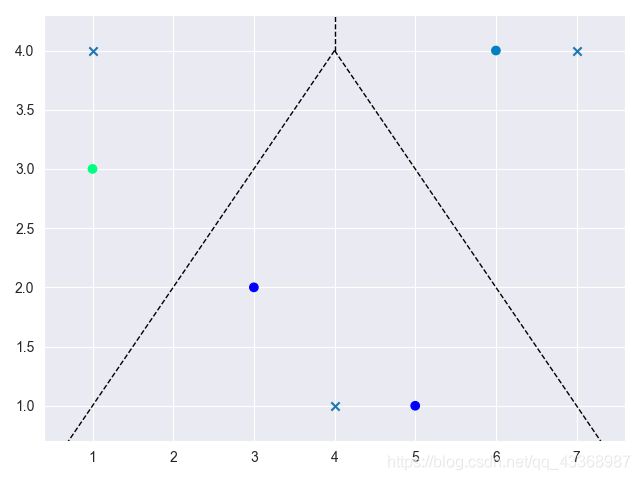
- 当K确定时,根据我们初始中心点选择的不同,最终的分类结果也不一样。
- 就像上述数据也可以按照下面的方式来划分
如图所示:

- K-Means算法非常强大,它在每一步的过程中都考虑到了整个数据集的数据。
- K-Means算法速度也很快,因为我们只计算数据和中心点之间距离。
- 因此,如果我们需要对全体数据集进行聚类,分成不同种类时,K-Means是一种好的方法。
1.1代码展示
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
# 导入k_means算法
from sklearn.cluster import KMeans
from scipy.spatial import Voronoi,voronoi_plot_2d
#创建玩具数据集,下面是不同玩具机器代号(第一个值)
#0-2:Action Figures
# 3-5:building blocks
# 6-8:cars
# 下面是不同适用年龄机器代号(第二个值)
# 0:5 year_olds
# 1:6 year_olds
# 2:7 year_olds
# 3:8 year_olds
# 4:9 year_olds
# 5:10 year_olds
# 创建数据及的数组
x=np.array([[0,4],[1,3], [2,5], [3,2], [4,0], [5,1], [6,4], [7,5], [8,3]])
# 用k-means算法建模,n_clusters代表K的值,random_stat确定质心初始化的随机数生成
kmeans=KMeans(n_clusters=3,random_state=0).fit(x)
# 画图
sns.set_style('darkgrid')
plt.scatter(x[:,0],x[:,1],c=kmeans.labels_,cmap=plt.get_cmap('winter'))
# 绘制群的边界和中心点
center=kmeans.cluster_centers_
plt.scatter(center[:,0],center[:,1],marker='x')
vor=Voronoi(center)
voronoi_plot_2d(vor,ax=plt.gca(),show_points=False,show_vertices=False)
# 设置坐标轴
plt.gca().set_xlim()
plt.gca().set_ylim()
plt.tight_layout()
plt.show()
2.Hierarchinak聚类
Hierarchical聚类(分层聚类/层次聚类/系统聚类)是将数据集想象成一个分层的数据结构。然后通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树
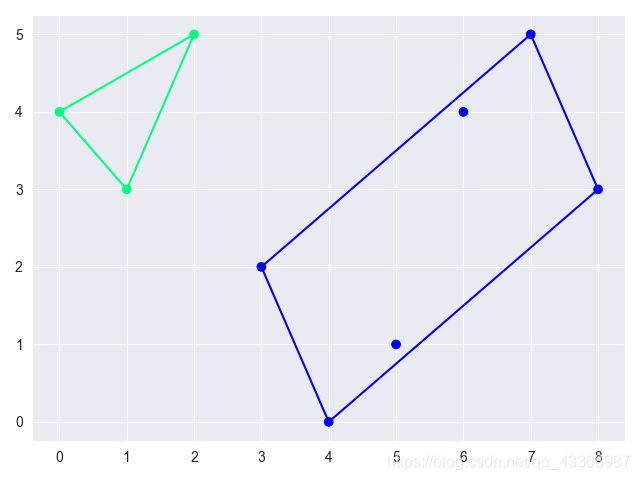
- 首先我们创建一个包含所有数据的集群,如图所示:

- 然后,在这个集群内部,我们找到两个最不相似的子集群并将它们拆分。我们通过计算簇间距离来确认合适的拆分,以使得簇间距离最大。
如图所示:
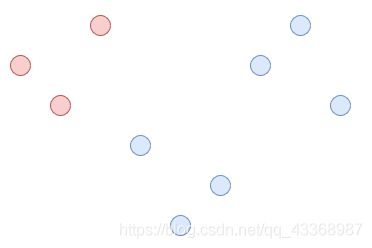
- 重复以上两步操作,直到所有的样本点都归为一类为止
上述方法被称为自上而下的分裂方法。
同理,我们也有自下而上的聚合方法:
- 我们可以首先将所有的数据点都看作为一簇集群。
- 然后将两个最近的集群合成一个更大的集群。(最近代表两簇集群的簇间距离最小)
- 我们持续上述操作,直至最后只有一个集群为止。
当然,无论是自上而下还是自下而上,我们都可以在适合的时候选择停止,从而获得最合适的聚类。
相比K-means来说,hierarchical显得比较缓慢,并不适合大型的数据。但是hierarchical并不需要预先给定聚类的类别数,而是在运行的过程中选择合适的类别。
2.1代码展示
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
# 导入k_means算法
from sklearn.cluster import KMeans
from scipy.spatial import Voronoi,voronoi_plot_2d
#创建玩具数据集,下面是不同玩具机器代号(第一个值)
#0-2:Action Figures
# 3-5:building blocks
# 6-8:cars
# 下面是不同适用年龄机器代号(第二个值)
# 0:5 year_olds
# 1:6 year_olds
# 2:7 year_olds
# 3:8 year_olds
# 4:9 year_olds
# 5:10 year_olds
# 创建数据及的数组
x=np.array([[0,4],[1,3], [2,5], [3,2], [4,0], [5,1], [6,4], [7,5], [8,3]])
# 用k-means算法建模,n_clusters代表K的值,random_stat确定质心初始化的随机数生成
kmeans=KMeans(n_clusters=3,random_state=0).fit(x)
# 画图
sns.set_style('darkgrid')
plt.scatter(x[:,0],x[:,1],c=kmeans.labels_,cmap=plt.get_cmap('winter'))
# 绘制群的边界和中心点
center=kmeans.cluster_centers_
plt.scatter(center[:,0],center[:,1],marker='x')
vor=Voronoi(center)
voronoi_plot_2d(vor,ax=plt.gca(),show_points=False,show_vertices=False)
# 设置坐标轴
plt.gca().set_xlim()
plt.gca().set_ylim()
plt.tight_layout()
plt.show()
四、小结
在本节中,我们学习了聚类和集群的相关知识。聚类可以让我们通过对相思数据点进行聚合,来对原始数据集进行分类。聚类是无监督学习中一种常见的算法,虽然它相对简单,但是功能强大。例如:我们可以使用居来进行购买人群分析,并且进行定向精准广告投放。对于企业来说,聚类是一个非常有用的技术。
自学自用,希望可以和大家积极沟通交流,小伙伴们加油鸭。创作不易,动起可爱的双手,来个赞再走呗 (๑◕ܫ←๑)