动态规划算法总结

动态规划

一：引入

(一)：棋盘问题

样例输出：3432

(二)：题目分析

1、题目要求：

​ 1、只能向右

​ 2、只能向下

​ 3、一次只能移动一步，且不能回退

2、分解

题目要求计算8x8 64棋盘的路线，如果直接正面冲，太难，且难以发现规律，那么我们可以将大的问题分解成若干较小的、容易解决的子问题，将这些问题解决了，那么大的问题就迎刃而解了。

根据这种处理思想，我们将8x8棋盘分解，先来观察2x2的棋盘：

我们可以发现，在2x2的情况下，到达（1，2）位置，只有1条路径，到达（2，1）位置也只有一条路径。

并且重要的一点是，我们可以发现想要到达终点（2，2）位置只能从（2，1）位置，或者从（1，2）位置到达。那么我们将从起点到达（1，2）位置的路径数与从起点到达（2，1）位置的路径数相加就是我们要求的从起点到终点的路径数

再来看3x3棋盘

我们可以根据上面得到的规律来递推，可以发现，所有行数为1的棋盘格子都只有一条路径，所有列数为1的格子也都只有一条路径。而其他的格子的路径数就是该格子的正上方格子路径数，加上该格子水平左方格子的路径数。

那么我们使用二维数组来模拟棋盘，那么可以得到递推公式

f[i][j] = f[i-1][j] + f[i][j-1];		//每一个数组中存储的就是到达该棋盘格子的路径总数

3、代码逻辑

得到递推公式，这个问题的核心问题就已经解决了，那么代码逻辑如下：

​ （1）、定义一个行列都为9的二维数组，因为我们0不用，所以定义为9

​ （2）、初始化边界信息，全部为1；

​ （3）、使用for循环嵌套，使用递推公式来计算每一个数据的值。

(三)：代码

void Test01(){
    //创建二维数组
    int f[9][9] = {0};      //将二维数组中的全部数据初始化为0

    //初始化边界情况
    for (int i = 0; i < 9; ++i) {
        f[1][i] = 1;
        f[i][1] = 1;
    }

    //双层循环嵌套
    for (int i = 2; i < 9 ; ++i) {
        for (int j = 2; j < 9 ; ++j) {
            f[i][j] = f[i-1][j] + f[i][j-1];
        }
    }
    cout<

结果：

二：动态规划

(一)：什么动态规划问题

定义：动态规划是运筹学的一个分支，是一种分阶段解决策略问题的最优解的数学思想。是对解最优化问题的一种途径、一种方法，而不是一种特殊的算法。

动态规划这类题都有共同的特点：

i、最优子结构

​ 母问题的最优解包含其子问题的最优解，所以我们称此问题具有最优子结构。

ii、子问题重叠

​ 举个例子：学校统计所有学生的身份证信息，但是整个学校的学生太多，所以可以统计每个班级学生的身份证信息，班级又可以拆分成一个一个的小组进行统计，那么统计小组和统计的过程是一样的，这就叫子问题重叠。

解决动态规划问题的一般模板：

​ 1、划分阶段：按照问题的特征，把问题分成若干个阶段

​ 2、确定状态和状态变量：将问题发展到各个阶段所处的各种情况用不同的状态表示出来

​ 3、确定决策并写出状态转移方程：根据相邻状态之间的关系确定决策

​ 4、寻找边界条件：递推式的边界条件

其中最困难的就是找到状态转移方程，如果状态转移方程能够正确找到，那么问题就解决了。

三：递推算法or递归算法or动态规划

上面对于棋盘问题的解决方式采用的就是动态规划，我们可以发现每一个阶段的结果都是依靠着前面某个阶段的结果来推导出的。那么可能大家会这样的疑问：好像动态规划和递归算法的思想是一样的，都是将一个大的问题划分成一个个小的问题的来处理，那是不是所有的递归问题都能用动态规划来解决?又或者所有的动态规划问题都可以使用递归算法来实现?递归算法和动态规划有区别吗？另外我们在解决动态规划问题时得到的状态转移方程，是不是又很像递推算法？那么动态规划与递推算法又有什么关系呢？

为了解决上面的问题，我们先来看看如何使用递归算法来实现棋盘问题

(一)：使用递归解决棋盘问题

递归分析：

​ 出口条件：i == 1 or j == 1;

​ 递归公式：fun(i,j) = fun(i-1,j) + fun(i,j-1);

​ 初始条件：i = 8,j = 8;

int Test02(int i,int j){
    if (i==1 || j == 1){
        return 1;
    }
    return Test02(i-1,j) + Test02(i,j-1);
}

我们发现使用递归同样得到问题的答案，并且使用递归实现的算法要比动态规划算法的代码要少很多。那是不是递归算法就比动态规划要好呢？并不是这样，我们来分析一下两者所用到的时间和空间复杂度

递归实现的方式，时间复杂度为O(2^{n)，而使用动态规划算法的时间复杂度为O(n}2)。

(二)：动态规划与递归算法的区别

主要共同点：

二者都要求原问题具有最优子结构性质，都是将原问题分而治之，分解成若干个规模较小（小到容易解决的程序）的子问题，然后将子问题的解合并，形成原问题的解

各自得实现方式：

分治法通常利用递归求解

动态规划通常利用迭代法自底向上进行求解，但也能用具有记忆功能得递归法自顶向下求解。

主要区别：

分治法将分解之后得子问题看成互相独立，子问题之间互不相交，然后在递归求解。

动态规划将分解之后得子问题理解为相互间有联系，有重叠部分。即动态规划把原问题分解成子问题，但是子问题中有公共的子问题，在计算问题的过程中把结果记录下来，然后在遇到相同的子问题时就可以不用计算，以此来提高计算速度。

(三)：动态规划与递推算法的区别

1、递推算法

​ 定义：指从已知的初始条件出发，按照某种递推关系，逐次推出所要求的各中间结果以及最后的结果。

​ 可用递推算法求解的问题一般有两种特点：

​ 1、问题可以划分成多个状态

​ 2、除初始状态之外，其他各个状态都可以使用固定的递推关系表达式来进行表示

​ 递推问题的求解步骤

​ 1、建立递推关系

​ 2、确定边界条件

​ 3、递推求解

2、动态规划与递推算法的区别

递推算法是一种计算机算法，通常用来将一个递推函数转换成一个线性或者多项式时间的求解程序

动态规划是一个运筹学算法，通常可以用来将一个满足特定条件的决策最优化问题转化成一个递推函数。

也就是说，动态规划解决的问题，通常都可以使用递推进行编码实现。如果问题本身就是个递推公式（譬如斐波那契数列），那就不应该称为动态规划

递推函数也不一定必须使用递推求解，特定类型的递推函数的求解除了递推以外，还有母问题、矩阵求幂等方法。只是大部分动态规划问题可能不满足这些解法的前提。必须用递推才能进行求解。

大学老师曾经说过一个比较简洁的理解：递推是一种解决问题的具体实现方法，而动态规划是将一个问题转换成递推方式解决的算法思路

四：动态规划算法例子

(一)：0-1背包

1、背包容量问题

(1)、题目描述

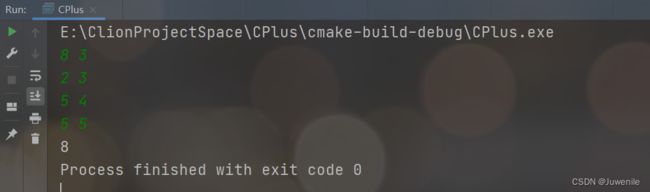
问题描述：有一个最多能够装入m千克的背包，此时有若干种宝物，每种宝物都有自己的重量w和价值c，并且每种宝物只有一种，请问，该背包最多能够装入价值为多少的宝物？

输入：第一行两个整数分别表示背包容量m和宝物数量n。接下来的n行，每一行有两个整数，表示该宝物的重量w和价值c

输出：一个整数，表示最多能装入价值多少的宝物

(2)、问题分析

根据解决动态规划问题的一般模板，先划分阶段，在划分状态，接着确定状态转移方程，最后确定边界信息。

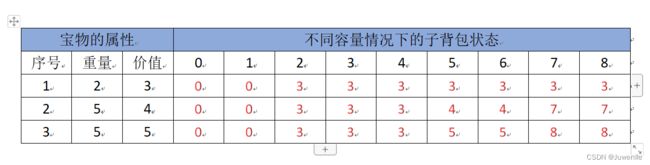
1、划分阶段：我们使用一个二维数组，行表示加入第几个宝物时的情况，列表示不同背包容量的情况。即每一阶段的状态。

2、确定每一阶段的状态，并确定状态值。

3、状态转移方程：我们将每个状态存放在数组 f[i][j]中，表示将第i个物品放入到背包容量为j的背包中，能够获得的最大价值。那么在计算f[i][j]时，就有两种情况：

该状态下的背包容量不够将宝物i放入的情况：如放入第1块宝物时，背包的容量为0或者1时，此时就放进去；又例如，当放入第2块宝物时，背包的容量为0，1，2，3，4时放不进去第2块宝物，那么此时的状态转移方程f[i][j] = f[i-1][j] 表示的就是不放入第i块宝物，也就是等于放入第i-1块宝物时的价值。

该状态下的背包容量够将宝物i放入的情况：此时又有两种情况，一种是放入第i块宝物时的价值更大，那么这时我们要注意背包中剩余的容量能不能将第i块宝物装入！就如在装入第2块宝物，背包的容量为5时，此时背包中已经有了重量为2，价值为3的第1块宝物，剩余的容量为3，并不足以将第2块宝物装入，所以我们要执行的操作就是将背包中的一些宝物倒出来，腾出空间来放入第2块宝物,此时的状态方程为：f[i][j] = f[i-1][j-w[i]]+c[i]; 另一种情况就是我们把第i块宝物放进背包之后的价值要比不放小，因为我们在放入第i块宝物时会将一些宝物倒出，腾出空间放入第i块宝物，那么倒出来的这些宝物的价值如果要比第i块宝物的价值高，那么把第i块宝物放入背包中的总价值就不妨要小了，那么此时的状态方程就是：f[i][j] = f[i-1][j]。

4、确定边界情况，初始化二维数组为0

(3)、代码

void Test01(){
    int f[10][10] = {0};        //创建二位数组，初始化为0
    int w[10],c[10];            //创建重量和价值数组，存储每一块宝石的重量和价值
    int m,n;                    //表示背包的容量和宝石的数量

    //输入数据
    cin>>m>>n;
    for (int i = 1; i <= n; ++i) {
        cin>>w[i]>>c[i];
    }

    //使用状态转移方程确定每一个阶段的状态值
    for (int i = 1; i <= n ; ++i) {
        for (int j = 1; j <= m ; ++j) {
            if (j>=w[i]){   //该状态下的背包容量能够将宝物i装入
                f[i][j] = max(f[i-1][j],f[i-1][j-w[i]]+c[i]);
            } else  {       //该状态下的背包容量装不下宝物i
                f[i][j] = f[i-1][j];
            }
        }
    }
    cout<

2、采药问题

(1)、题目描述

问题描述：山洞里面有一些不同的草药，采每一株都需要一些时间，每一株也有自身的价值，现在给定时间，在给定的时间内，让采到的草药总价值最大，每种草药的数量只有一株。

(2)、分析

此题与上一道题基本一样。

背包容量问题	采药问题
背包容量为m	给定时间
宝物有自己的重量	采每一株草药需要时间
宝物有自己的价值	每一株草药有自己的价值
求背包价值最大	求所采草药的最大价值

因此这里代码可以参考上一题

(二)：完全背包

1、分配方案问题

(1)、题目描述

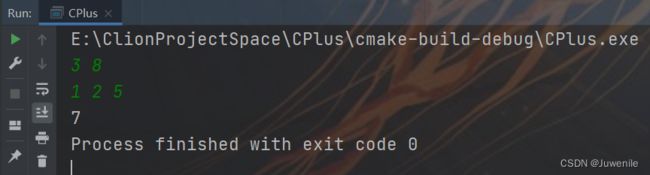
题目描述：现在有v种不同的宝石，假设每一种宝物的数量都是无限的，并且每一种宝石都有各自价格，有一位买家带了n元钱，现在这位买家想要用这n元钱来购买宝石，请求出买家有多少种购买方式？

输入：第一行两个整数v，n分别表示宝石种类数，以及买家带的钱。第二行有v个整数，分别表示v种宝石的价值

输出：购买方式数

(2)、分析

根据解决动态规划问题的一般模板，先划分阶段，在划分状态，接着确定状态转移方程，最后确定边界信息。

1、划分阶段：我们使用一个二维数组，行表示加入第几个宝物时的情况，列表示不同钱数的情况。即每一阶段的状态。第一行表示的是只够买第一种宝物的情况，因此无论钱数是多少，购买方案都只有1种

2、确定每一阶段的状态，并确定状态值。

3、确定状态转移方程：使用一个二维数组将每个状态值存在f[i][j]中，表示用第i种宝石组合出价值为j时，能够成功的方案总数，也就是买家的购买方案数量。那么在计算f[i][j]时，就有两种情况：

该状态钱不购买第i块宝石情况：此时的购买方案与买第i-1块宝石时的购买方案一样，所以f[i][j] = f[i-1][j]

该状态下钱购买第i块宝石情况：此时的购买方案由两部分组成，一是不买第i块宝石时的方案，即f[i-1][j]；二是买第i块宝石，但是在购买的钱数为 j-c[i] 的情况下的购买方案，即f[i][j-c[i]]

4、确定边界情况：可以发现当只有第1块宝石时的销售方案全是1，并且当钱数n为0的时候，按照现实情况应该是0，但是为了后面的推导，这里全部设置成1。

(3)、代码

void Test02(){
     int f[5][10] = {0};    //创建二位数组
     int c[5] = {0};         //存储每块石头的价值
     int v;           //石头的数量
     int n;         //买家的钱
     //输入石头的数量和买家的钱
     cin>>v>>n;
     //输入每种石头的所需要的钱，并初始化二维数组
     for (int i = 1; i <= v ; ++i) {
         cin>>c[i];     //对应石头的价值
         f[i][0] = 1;   //初试化数值
     }

     //逻辑代码
     for (int i = 1; i <= v ; ++i) {
         for (int j = 1; j <= n ; ++j) {
             if (j>=c[i]){   //放置数组下标越界
                 f[i][j] = f[i-1][j] + f[i][j-c[i]];    //状态转移方程
             } else{
                 f[i][j] = f[i-1][j];
             }
         }
     }
     cout<

2、货币系统

(1)、题目描述

问题描述：现在有v种不同面值的货币，每种货币的数量不限，求组成总面值为n的货币有多少种不同的方案？

输入：第一行有两个整数，分别表示v种不同面值的货币，和总面值n

输出：表示总分配方案数

(2)、分析

货币问题与上面的分配方案问题解决思路是一样的。

货币问题	0-1背包问题
v种不同面值的货币	有v不同价值的宝石
数量不限	数量不限
总面值为n	买家带了n元钱
多少种不同的方案	多少种购买方案

代码也与上题类似，可以借鉴上一题

(三)：0-1背包与完全背包

通过上面的题目描述可以得知0-1背包最大的特点就是每种物品都只有一种，即只能使用一次，但是完全背包中每种物品的数量是无限的

五：空间优化

(一)：空间优化概述

一般情况下动态规划算法的策略就是空间换时间，所以一般情况下的动态规划问题我们需要创建一个二维数组，也就是开辟一个空间复杂度为O(n^{2)**的辅助数组，用于存放每一个状态（子问题）的最优解。但是多数的动态规划问题可以进行空间优化，把**O(n}2） -> O(n).

我们可以观察一下在我们使用二维数组进行推导状态转移方程的过程。可以发现我们想要获得加入第i宝石时各个状态下的最优解，会用到在加入第i-1块宝石时已经得到的最优解，即在二维数组中获取第i行数据时，我们需要用到数组中第i-1行的数据，但是第i-2行，及之前的数据都用不到，那么这些数据就是在白白的浪费空间。

既然如此，我们可以使用一维数组来存储加入第i-1块宝石时，各个阶段获得的最优解，那么在计算加入第i块宝石各阶段的最优解时就可以之间在这个一维数组中进行更新和替换，而不需要用到二维数组。

(二)：一维状态转移方程

我们使用一维数组来存储各阶段的最优解时，那么我们的状态转移方程就需要进行更改。

以0-1背包为例：

f[i][j] = max(f[i-1][j] , f[i-1][j-w[i]] + c[i]);

f[i-1][j]：表示不加入第i块宝物时，背包中的总价值量。在二维数组中也就是f[i][j]的正上方数据。那么在一维数组中表示就是该元素自身：f[j]

f[i-1][j - w[i]] + c[i]:表示要加入第i块宝物后背包中的总价值。那么在一维数组中表示的就是f[j-w[i]] + c[i]

因此，一维数组的状态状态转移方程就是：

f[j] = max(f[j],f[j-w[i]] + c[i]);

(三)：空间优化后的0-1背包

得到状态转移方程之后，我们来使用代码实现一下空间优化之后的0-1背包问题

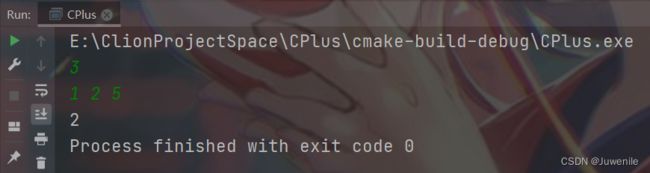
void Test03(){
    int f[10] = {0};  //创建一维背包数组
    int w[5],c[5];
    int m,n;
    //输入数据
    cin>>m>>n;
    for(int i=1;i<=n;i++){
        cin>>w[i]>>c[i];
    }
    
    for (int i = 1; i <= n; ++i) {
        for (int j = m; j >=0 ; j--) {	//注意：与二维数组不同，内层嵌套需要从后向前进行，否则会重复将某一块宝石装入背包
            if (j>w[i]){
                f[j] = max(f[j],f[j-w[i]]+c[i]);
            }
        }
    }
    cout<

注意：与二维数组不同，内层嵌套需要从后向前进行，否则会重复将某一块宝石装入背包。可以试着使用一维状态转移方程，从前往后推到出每一个阶段的状态值，然后与从后向前推导每一个阶段的状态值进行对比。

(四)、猴子拔河问题

1、问题描述

有n只猴子的力量之数据，现在要求将这些猴子分成两组， 使这两组猴子总力量值之差达到最小，请求出这个最小值

输入：第一行一个整数表示猴子的数量。第二行n个整数，表示每只猴子的力量值

输出：一行，表示分成两组之后，两组猴子总力量值之差的最小值

2、分析

题目要求出两组猴子力量值差的最小值，最理想的状态是，两组猴子的力量值相同，即每一组猴子的力量总和是所有猴子力量总和的一半，那么差值就是0。在一般情况下，要求出差值最小的情况，那一定是两组猴子的力量总和都很接近所有猴子力量和的一半。

那么这道题其实就等价于：从n只猴子中取出若干只，使这些猴子的力量和最大，但是不能超过n只猴子力量和的一半。

因此这道题就是一个动态规划问题了，并且与0-1背包处理过程一致

猴子问题	0-1背包问题
n只猴子	n种不同的宝石
每只猴子都有力量值	每种宝石都有各自的价值
力量和最大	使得背包中的价值最大
力量和不能超过n只猴子力量和的一半	背包容量最大为m

因此该问题的状态转移方程与0-1背包的状态转移方程一致：

 dp[j] = max(dp[j],dp[j-monkey[i]] + monkey[i]);

3、代码

int monkey[20];           //用来存储每只猴子的力量值
int mmin = 2147483647;       //mmin表示差最小
int dp[20];
int main(){
    int n;      //表示猴子的数量
    int sum = 0;    //表示猴子的力量总和

    cin>>n;
    //输入力量值并求和
    for (int i = 1; i <= n ; ++i) {
        cin>>monkey[i];
        sum+=monkey[i];         //计算力量总和
    }

    //将问题转换成背包问题：将n只猴子分成一支力量不超过sum/2的队伍：循环处理对应的数据
    for (int i = 1; i <= n ; ++i) {
        for (int j = sum/2; j >= monkey[i] ; j--) {
            //是否装入第i个数据，寻找装入后是否更大
            dp[j] = max(dp[j],dp[j-monkey[i]] + monkey[i]);
        }
    }

    //在所有的情况中，找出差值最小的
    mmin = sum - dp[sum/2]*2;
    cout<

4、结果