python 三种聚类算法(K-means,AGNES,DBScan)
python实现鸢尾花三种聚类算法(K-means,AGNES,DBScan)
更新时间:2019年06月27日 14:44:44 作者:weixin_42134141
这篇文章主要介绍了python实现鸢尾花三种聚类算法(K-means,AGNES,DBScan),文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧
一.分散性聚类(kmeans)
算法流程:
1.选择聚类的个数k.
2.任意产生k个聚类,然后确定聚类中心,或者直接生成k个中心。
3.对每个点确定其聚类中心点。
4.再计算其聚类新中心。
5.重复以上步骤直到满足收敛要求。(通常就是确定的中心点不再改变。
优点:
1.是解决聚类问题的一种经典算法,简单、快速
2.对处理大数据集,该算法保持可伸缩性和高效率
3.当结果簇是密集的,它的效果较好
缺点
1.在簇的平均值可被定义的情况下才能使用,可能不适用于某些应用
2.必须事先给出k(要生成的簇的数目),而且对初值敏感,对于不同的初始值,可能会导致不同结果。
3.不适合于发现非凸形状的簇或者大小差别很大的簇
4.对躁声和孤立点数据敏感
这里为了看鸢尾花的三种聚类算法的直观区别,所以不用具体算法实现,只需要调用相应函数即可。
程序如下:
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:, :4] # #表示我们取特征空间中的4个维度
print(X.shape)
# 绘制数据分布图
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='see')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
estimator = KMeans(n_clusters=3) # 构造聚类器
estimator.fit(X) # 聚类
label_pred = estimator.labels_ # 获取聚类标签
# 绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()运行结果:
二.结构性聚类(层次聚类)
1.凝聚层次聚类:AGNES算法(自底向上)
首先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到某个终结条件被满足
2.分裂层次聚类:DIANA算法(自顶向下)
首先将所有对象置于一个簇中,然后逐渐细分为越来越小的簇,直到达到了某个终结条件。
这里我选择的AGNES算法。
程序如下:
from sklearn import datasets
from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
import pandas as pd
iris = datasets.load_iris()
irisdata = iris.data
clustering = AgglomerativeClustering(linkage='ward', n_clusters=3)
res = clustering.fit(irisdata)
print ("各个簇的样本数目:")
print (pd.Series(clustering.labels_).value_counts())
print ("聚类结果:")
print (confusion_matrix(iris.target, clustering.labels_))
plt.figure()
d0 = irisdata[clustering.labels_ == 0]
plt.plot(d0[:, 0], d0[:, 1], 'r.')
d1 = irisdata[clustering.labels_ == 1]
plt.plot(d1[:, 0], d1[:, 1], 'go')
d2 = irisdata[clustering.labels_ == 2]
plt.plot(d2[:, 0], d2[:, 1], 'b*')
plt.xlabel("Sepal.Length")
plt.ylabel("Sepal.Width")
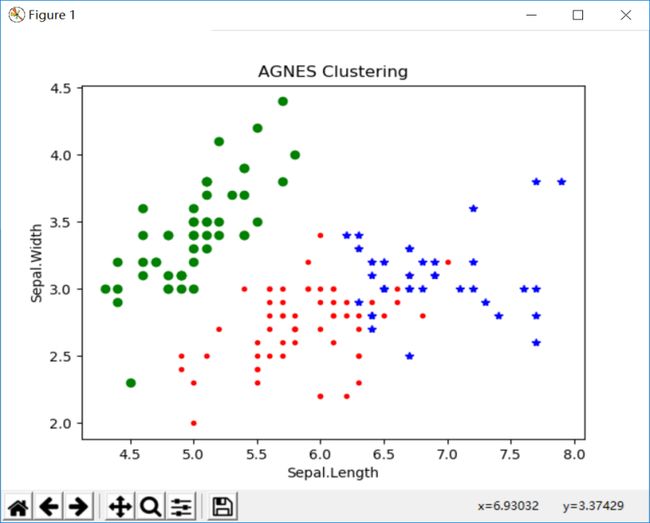
plt.title("AGNES Clustering")
plt.show()运行结果:
三.密度聚类之DBSCAN算法:
算法:
需要两个参数:ε (eps) 和形成高密度区域所需要的最少点数 (minPts)
它由一个任意未被访问的点开始,然后探索这个点的 ε-邻域,如果 ε-邻域里有足够的点,则建立一个新的聚类,否则这个点被标签为杂音。注意这个点之后可能被发现在其它点的 ε-邻域里,而该 ε-邻域可能有足够的点,届时这个点会被加入该聚类中。
程序如下:
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans
from sklearn import datasets
from sklearn.cluster import DBSCAN
iris = datasets.load_iris()
X = iris.data[:, :4] # #表示我们只取特征空间中的4个维度
print(X.shape)
# 绘制数据分布图
plt.scatter(X[:, 0], X[:, 1], c="red", marker='o', label='see')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
plt.show()
dbscan = DBSCAN(eps=0.4, min_samples=9)
dbscan.fit(X)
label_pred = dbscan.labels_
# 绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c="red", marker='o', label='label0')
plt.scatter(x1[:, 0], x1[:, 1], c="green", marker='*', label='label1')
plt.scatter(x2[:, 0], x2[:, 1], c="blue", marker='+', label='label2')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend(loc=2)
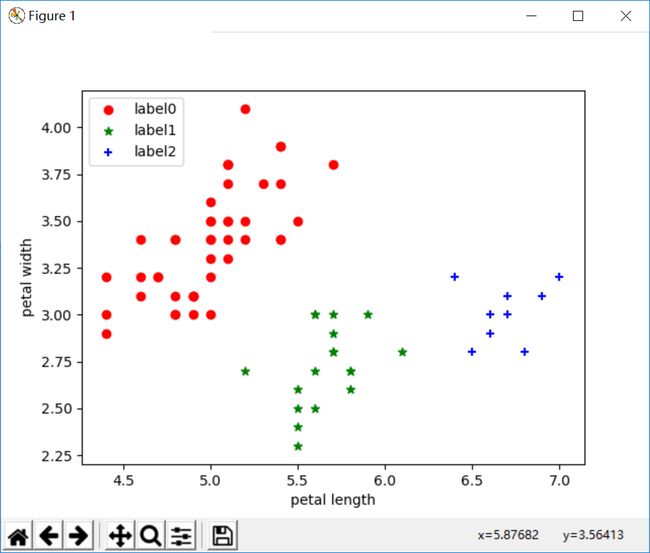
plt.show()运行结果:
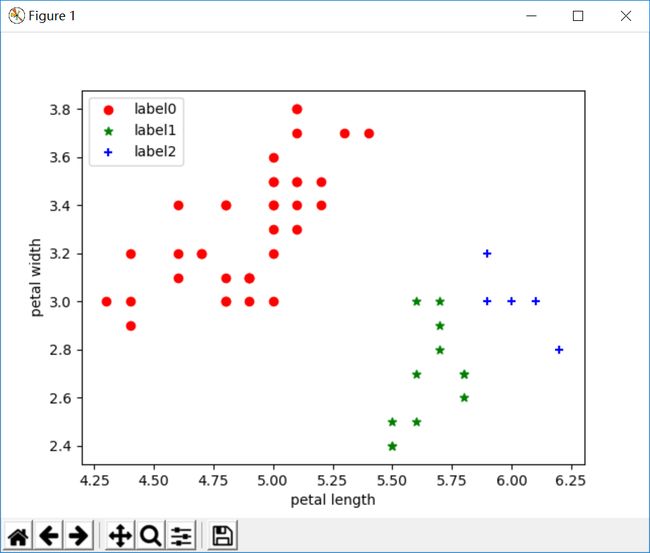
改变参数后:
四、结果分析
从上面三种实验截图可以看出,k-means聚类和AGNES层次聚类分析结果差不多的三类,与DBSCAN的结果不一样。为啥不一样,这就取决于算法本身的优缺点了。
k-means对于大型数据集也是简单高效、时间复杂度、空间复杂度低。 最重要是数据集大时结果容易局部最优;需要预先设定K值,对最先的K个点选取很敏感;对噪声和离群值非常敏感;只用于numerical类型数据;不能解决非凸数据。
DBSCAN对噪声不敏感;能发现任意形状的聚类。 但是聚类的结果与参数有很大的关系;DBSCAN用固定参数识别聚类,但当聚类的稀疏程度不同时,相同的判定标准可能会破坏聚类的自然结构,即较稀的聚类会被划分为多个类或密度较大且离得较近的类会被合并成一个聚类。
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持脚本之家。